目录
问题讨论
01背包问题公式
为什么状态压缩到一维时候需要逆序?
怎样求次数?
转化成最大和sum/2的01背包:LeetCode.416.分割等和子集
转化成最大和sum/2的01背包:LeetCode1049.最后一块石头的重量II
LeetCode.494.目标和
回溯超时
转换成01背包
LeetCode.474.一和零
阿里笔试原题:LeetCode.879.盈利计划
问题讨论
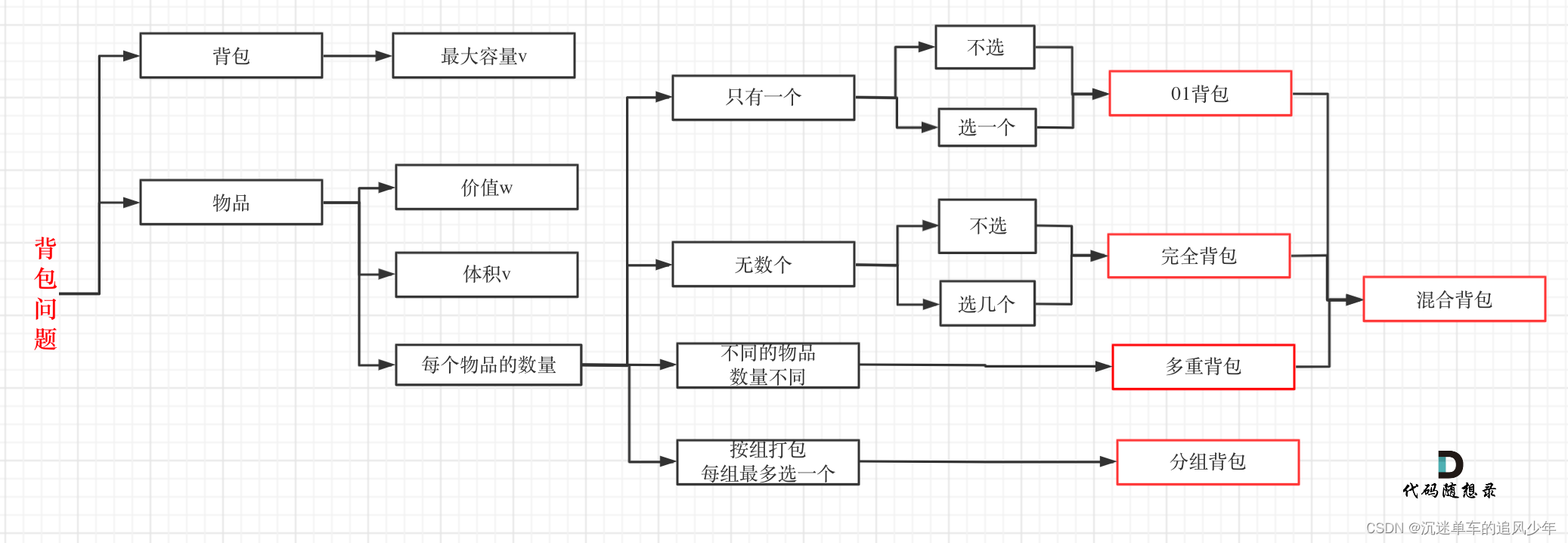
01背包问题公式
dp[j]为 容量为j的背包所背的最大价值,dp[j]可以通过dp[j - weight[i]]推导出来,dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。dp[j - weight[i]] + value[i] 表示 容量为 j - 物品i重量 的背包 加上 物品i的价值。(也就是容量为j的背包,放入物品i了之后的价值即:dp[j])。
此时dp[j]有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放物品i,一个是取dp[j - weight[i]] + value[i],即放物品i,指定是取最大的,毕竟是求最大价值,所以递归公式为:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);第一层是正序遍历,第二层逆序遍历,完整代码如下:
void test_1_wei_bag_problem() {
vector<int> weight = {1, 3, 4};
vector<int> value = {15, 20, 30};
int bagWeight = 4;
// 初始化
vector<int> dp(bagWeight + 1, 0);
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
cout << dp[bagWeight] << endl;
}为什么状态压缩到一维时候需要逆序?
压缩到一维时,要采用逆序。因为在一维情况下,是根据 dp[j] || dp[j - nums[i]]来推d[j]的值,如不逆序,就无法保证在外循环 i 值保持不变 j 值递增的情况下,dp[j - num[i]]的值不会被当前所放入的nums[i]所修改,当j值未到达临界条件前,会一直被nums[i]影响,也即是可能重复的放入了多次nums[i],为了避免前面对后面产生影响,故用逆序。 举个例子,数组为[2,2,3,5],要找和为6的组合,i = 0时,dp[2]为真,当i自增到1,j = 4时,nums[i] = 2,dp[4] = dp[4] || dp[4 - 2]为true,当i不变,j = 6时,dp[6] = dp [6] || dp [6 - 2],而dp[4]为true,所以dp[6] = true,显然是错误的。 故必须得纠正在正序情况下,i值不变时多次放入nums[i]的情况。
怎样求次数?
有的时候我们并不是要求出是否能装满容量为x的背包,dp[j] 表示:填满j(包括j)这么大容积的包,有dp[j]种方法。如果求凑成dp[j]总共有多少种方法呢?只需要把所有的 dp[j - nums[i]] 累加起来。用公式表达为:
dp[j] += dp[j - nums[i]]一定要注意需要初始化:
dp[0] = 1转化成最大和sum/2的01背包:LeetCode.416.分割等和子集

class Solution {
public:
bool canPartition(vector<int>& nums) {
int sumNum = 0;
for (auto num : nums)
sumNum += num;
// 和为奇数肯定不能够被分割
if (sumNum % 2 ==1)
return false;
// 转换成和为sum/2的01背包问题
int target = sumNum / 2;
vector<int> dp(target + 1, 0);
for (int i = 0; i < nums.size(); i++) {
for (int j = target; j >= nums[i]; j--) {
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
}
}
return dp[target] == target;
}
};转化成最大和sum/2的01背包:LeetCode1049.最后一块石头的重量II

class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
// 和416思路相似
// 转换成01背包问题,求两堆石头的最小差值。由于石头总和为sum.则问题转换成了
// 背包最多装sum / 2的石头,stones数组里有一大堆石头。求如何装能装下最多重量石头。
int sum = 0;
for (auto stone : stones) sum += stone;
int target = sum / 2;
vector<int> dp(target + 1, 0);
for (int i = 0; i < stones.size(); i++) {
for (int j = target; j >= stones[i]; j--) {
dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum - dp[target] - dp[target];
}
};LeetCode.494.目标和

回溯超时
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int S) {
// 通过递归列举出所有情况,超时
help(nums, 0, 0, S);
return count;
}
private:
int count = 0;
void help (vector<int> nums, int i, int sum, int S) {
if (i == nums.size()) {
if (sum == S) {
count++;
}
} else {
help(nums, i + 1, sum + nums[i], S);
help(nums, i + 1, sum - nums[i], S);
}
}
};转换成01背包
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
// nums可以分成x1和x2两个部分,x1+x2=sum,x1-x2=target
// 所以x1=(sum+target)/2
int sum = std::accumulate(nums.begin(), nums.end(), 0);
vector<int> dp(abs(target + sum) / 2 + 1, 0);
if ((sum + target) % 2 != 0 || abs(target) > sum) {
return 0;
}
dp[0] = 1;
for (int i = 0; i < nums.size(); i++) {
for (int j = (sum + target) / 2; j >= nums[i]; j--) {
dp[j] += dp[j - nums[i]];
}
}
return dp[(sum + target) / 2];
}
};LeetCode.474.一和零
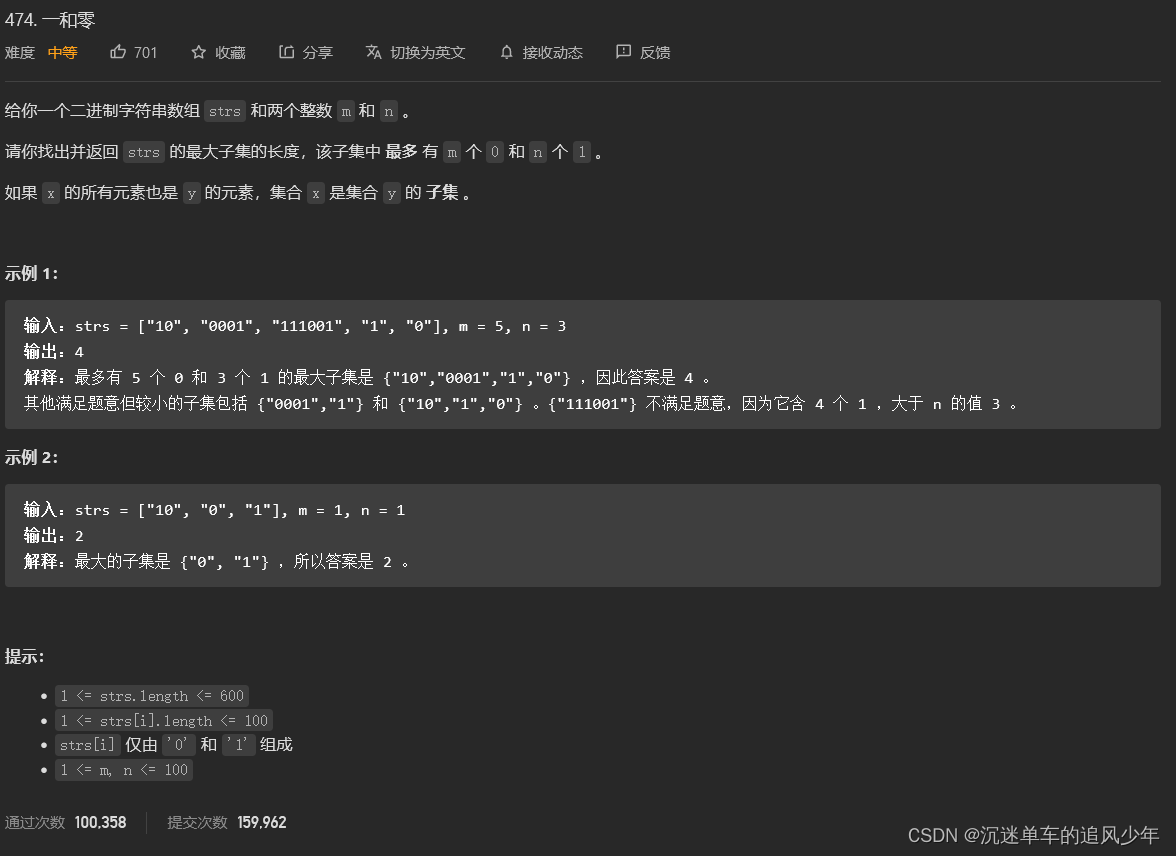
其实是一个三维DP,但是状态压缩了,所以两次遍历都需要是逆序遍历。
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
// https://programmercarl.com/0474.%E4%B8%80%E5%92%8C%E9%9B%B6.html#%E6%80%9D%E8%B7%AF
vector<vector<int> > dp(m + 1, vector<int> (n + 1, 0));
for (auto str : strs) {
int zeronum = 0;
int onenum = 0;
for (auto c : str) {
if (c == '0') {
zeronum ++;
} else {
onenum ++;
}
}
for (int i = m; i >= zeronum; i--) { // 从后向前遍历
for (int j = n; j >= onenum; j--) {
dp[i][j] = max(dp[i][j], dp[i - zeronum][j - onenum] + 1);
}
}
}
return dp[m][n];
}
};阿里笔试原题:LeetCode.879.盈利计划


暂时没有做出来,我好菜啊。。。