Python每日一练(20230422)

news2025/10/31 4:15:07

1. 杨辉三角 🌟

2. 最长回文子串 🌟🌟

3. 逆波兰表达式求值 🌟🌟

🌟 每日一练刷题专栏 🌟

Golang每日一练专栏

Python每日一练专栏

C/C++每日一练专栏

Java每日一练专栏

1. 杨辉三角

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

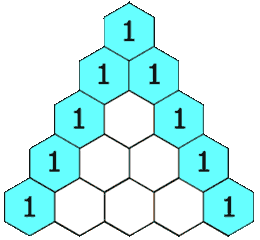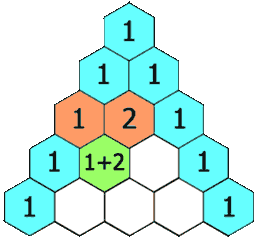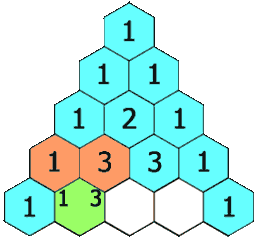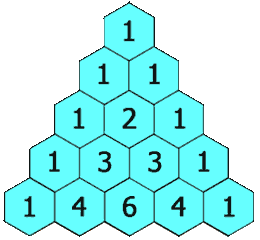
示例 1:

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2:

输入: numRows = 1
输出: [[1]]

提示:

1 <= numRows <= 30

出处：

https://edu.csdn.net/practice/26235120

代码：

from typing import List
class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        if numRows == 0:
            return []
        if numRows == 1:
            return [[1]]
        if numRows == 2:
            return [[1], [1, 1]]
        result = [[1], [1, 1]] + [[] for i in range(numRows - 2)]
        for i in range(2, numRows):
            for j in range(i + 1):
                if j == 0 or j == i:
                    result[i].append(1)
                else:
                    result[i].append(result[i - 1][j - 1] + result[i - 1][j])
        return result

if __name__ == "__main__":
    s = Solution()
    for i in range(1,6):
        print(s.generate(i))

输出：

[[1]]
[[1], [1, 1]]
[[1], [1, 1], [1, 2, 1]]
[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1]]
[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1], [1, 4, 6, 4, 1]]

2. 最长回文子串

给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

输入：s = "cbbd"
输出："bb"

示例 3：

输入：s = "a"
输出："a"

示例 4：

输入：s = "ac"
输出："a"

提示：

1 <= s.length <= 1000
s 仅由数字和英文字母（大写和/或小写）组成

出处：

https://edu.csdn.net/practice/26235121

代码：

class Solution:
    def longestPalindrome(self, s: str) -> str:
        ti = 0
        maxlen = 0
        i = 0
        while i < len(s):
            t = 1
            while t <= i and i + t < len(s):
                if s[i + t] == s[i - t]:
                    t += 1
                else:
                    break
            t -= 1
            if 2 * t + 1 > maxlen:
                ti = i - t
                maxlen = 2 * t + 1
            i += 1
        i = 0
        while i < len(s):
            t = 1
            while t <= i + 1 and i + t < len(s):
                if s[i - t + 1] == s[i + t]:
                    t += 1
                else:
                    break
            t -= 1
            if 2 * t > maxlen:
                ti = i - t + 1
                maxlen = 2 * t
            i += 1
        return s[ti:ti+maxlen]
# %%
s = Solution()
print(s.longestPalindrome('babad'))
print(s.longestPalindrome('cbbd'))

输出：

bab
bb

3. 逆波兰表达式求值

根据 逆波兰表示法，求表达式的值。

有效的算符包括 +、-、*、/ 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

说明：

整数除法只保留整数部分。
给定逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。

示例 1：

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例 3：

输入：tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出：22
解释：
该算式转化为常见的中缀算术表达式为：
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

提示：

1 <= tokens.length <= 10^4
tokens[i] 要么是一个算符（"+"、"-"、"*" 或 "/"），要么是一个在范围 [-200, 200] 内的整数

逆波兰表达式：

逆波兰表达式是一种后缀表达式，所谓后缀就是指算符写在后面。

平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。
该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。

逆波兰表达式主要有以下两个优点：

去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中。

出处：

https://edu.csdn.net/practice/26235122

代码：

class Solution(object):
    def evalRPN(self, tokens):
        """
        :type tokens: List[str]
        :rtype: int
        """
        stack = []
        for token in tokens:
            if token not in ["+", "-", "*", "/"]:
                stack.append(int(token))
            else:
                num1 = stack.pop()
                num2 = stack.pop()
                if token == "+":
                    stack.append(num1 + num2)
                elif token == "-":
                    stack.append(num2 - num1)
                elif token == "*":
                    stack.append(num1 * num2)
                elif token == "/":
                    if num1 * num2 < 0:
                        result = -((-num2) // num1)
                        stack.append(result)
                    else:
                        stack.append(num2 // num1)
            #print(stack)
        return stack.pop()
# %%
s = Solution()
print(s.evalRPN(tokens = ["2","1","+","3","*"]))
print(s.evalRPN(tokens = ["4","13","5","/","+"]))
tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
print(s.evalRPN(tokens))

输出：

9
6
22