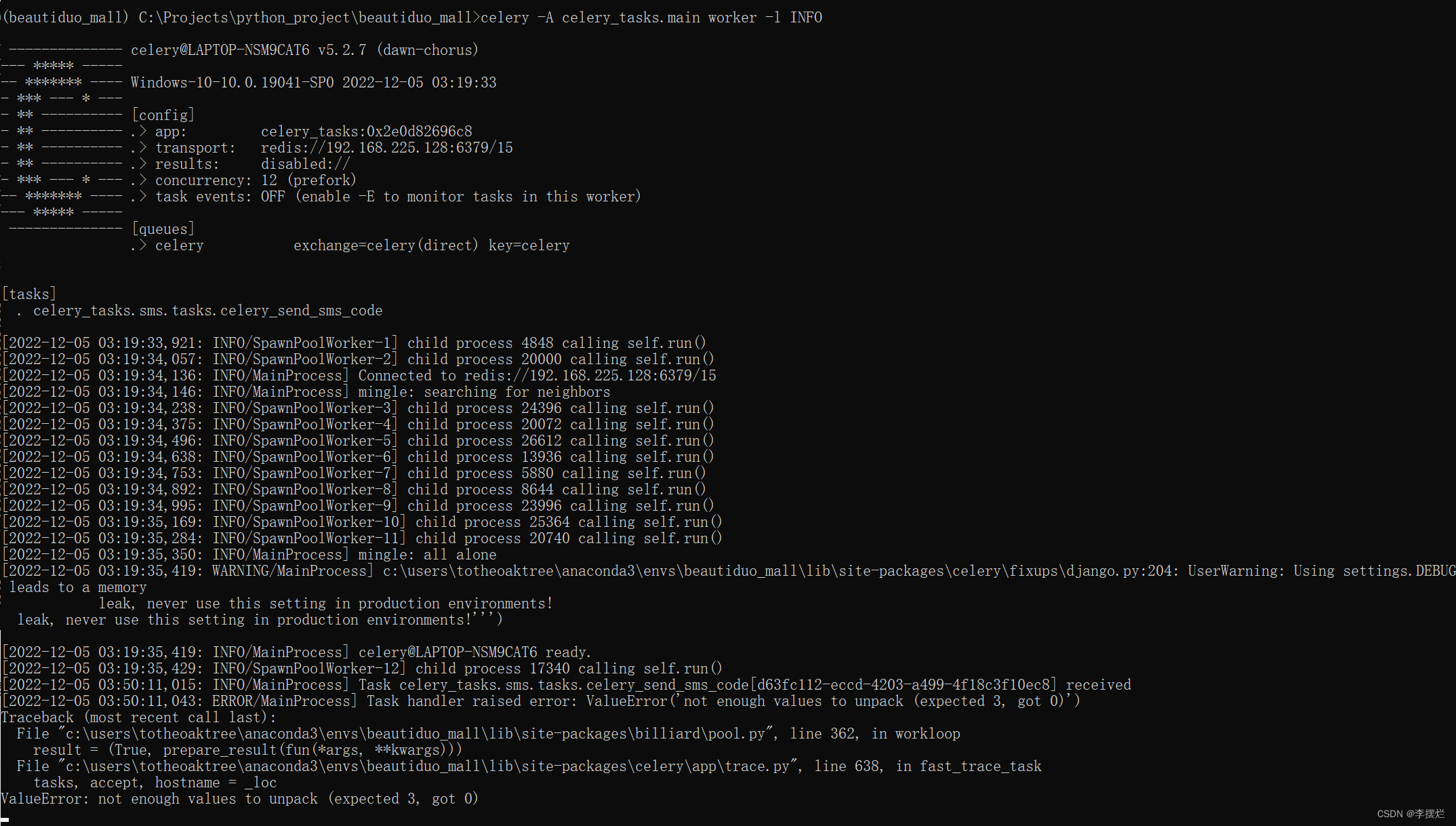
光流法Optical Flow,Lucas-Kanade方法,CV中光流的约束分析
- Multiple View Geometry
- 1. Optical Flow Estimation
- 2. The Lucas-Kanade Method
- 2.1 Brightness Constancy Assumption
- 2.2 Constant motion in a neighborhood
- 2.3 Compute the velocity vector
- 2.4 KLT tracker
- 3. Robust feature point extraction: Harris Corner detector.
- 4. Eliminate the brightness changes.
Multiple View Geometry
本文主要介绍计算机视觉中,光流法Optical Flow Method,Lucas-Kanade方法的约束,CV中光流的约束分析,包括了亮度不变约束,速度向量计算等方法。
1. Optical Flow Estimation
Optical Flow is suitable for small deformation, small displacement. Finding correspondence and tracking.
2. The Lucas-Kanade Method
2.1 Brightness Constancy Assumption
Let
x
(
t
)
x(t)
x(t) denote a moving point at time
t
t
t, and
I
(
x
,
t
)
I(x,t)
I(x,t) a video sequence, then:
I
(
x
(
t
)
,
t
)
=
C
o
n
s
t
.
∀
t
.
I(x(t),t)=Const. \forall t.
I(x(t),t)=Const.∀t.
i.e., the brightness of point
x
(
t
)
x(t)
x(t) is constant. Therefore the total time derivate must be zero:
d
d
(
t
)
I
(
x
(
t
)
,
t
)
=
∇
I
T
(
d
x
d
t
)
+
∂
I
∂
t
=
0
\frac{d}{d(t)}I(x(t),t)=\nabla I^T (\frac{dx}{dt})+\frac{\partial I}{\partial t}=0
d(t)dI(x(t),t)=∇IT(dtdx)+∂t∂I=0
This constraint is often called the optical flow constraint. The desired local flow vector (velocity) is given by
v
=
d
x
d
t
v=\frac{dx}{dt}
v=dtdx.
Prof: the derivative of d I d x d x d t \frac{dI}{dx}\frac{dx}{dt} dxdIdtdx, where the first component is ∇ I \nabla I ∇I is ( ∂ I ∂ x , ∂ I ∂ y ) T (\frac{\partial I}{\partial x},\frac{\partial I}{\partial y})^T (∂x∂I,∂y∂I)T.
So, the first component can be described as: this is the flow vector v v v, (which represents the movement direction), projection on the image gradient ∇ I \nabla I ∇I .
∇ I \nabla I ∇I Is the spatial brightness derivative, ∂ I ∂ t \frac{\partial I}{\partial t} ∂t∂I is the temporal brightness derivative, d x d t \frac{dx}{dt} dtdx is the velocity vector.


2.2 Constant motion in a neighborhood
One assumes that
v
v
v is constant over a neighborhood window
W
(
x
)
W(x)
W(x) of the point
x
x
x:
∇
I
(
x
′
,
t
)
T
v
+
∂
I
∂
t
(
x
′
,
t
)
=
0
,
∀
x
′
∈
W
(
x
)
.
\nabla I(x',t)^T v + \frac{\partial I}{\partial t}(x',t)=0, \quad \forall x'\in W(x).
∇I(x′,t)Tv+∂t∂I(x′,t)=0,∀x′∈W(x).
2.3 Compute the velocity vector
Compute the best velocity vector
v
v
v for the point
x
x
x by minimizing the least square error:
E
(
v
)
=
∫
W
(
x
)
∣
∇
I
(
x
′
,
t
)
T
v
+
I
t
(
x
′
,
t
)
∣
2
d
x
′
.
E(v)=\int_{W(x)}\left| \nabla I(x',t)^Tv+I_t(x',t)\right|^2dx'.
E(v)=∫W(x)
∇I(x′,t)Tv+It(x′,t)
2dx′.
Setting the derivative to zero we obtains:
d
E
d
v
=
2
M
v
+
2
q
=
0
\frac{dE}{dv}=2Mv+2q=0
dvdE=2Mv+2q=0

2.4 KLT tracker
KLT tracker. A simple feature tracking algorithm. However, this is not reliable. When the contrast or the image pixel deviation in a low manner, the gradient is easy to be zero, which make the M ( x ) M(x) M(x) is easy to un-invertible, which can not guarantee to be larger than a threshold. So, these tracking points are no longer useful, we should find another pixel points to initial as new tracking points.

Even d e t ( M ) ≠ 0 det(M)\neq 0 det(M)=0, dose not guarantee robust estimates of velocity, the inverse of M ( x ) M(x) M(x) may not stable if d e t ( M ) det(M) det(M) is very small.
3. Robust feature point extraction: Harris Corner detector.
So, to guarantee robust estimation of velocity, a robust feature point extraction algorithm has been proposed. Named Harris Corner extraction.

4. Eliminate the brightness changes.
-
Since the motion is no longer translational, one need to generalize the motion model for window W ( x ) W(x) W(x), so, we can use affine motion model or homograph motion model.
-
Robust to illumination changes.
We can use Normalized Cross Correlation to reduce the intensity changes.