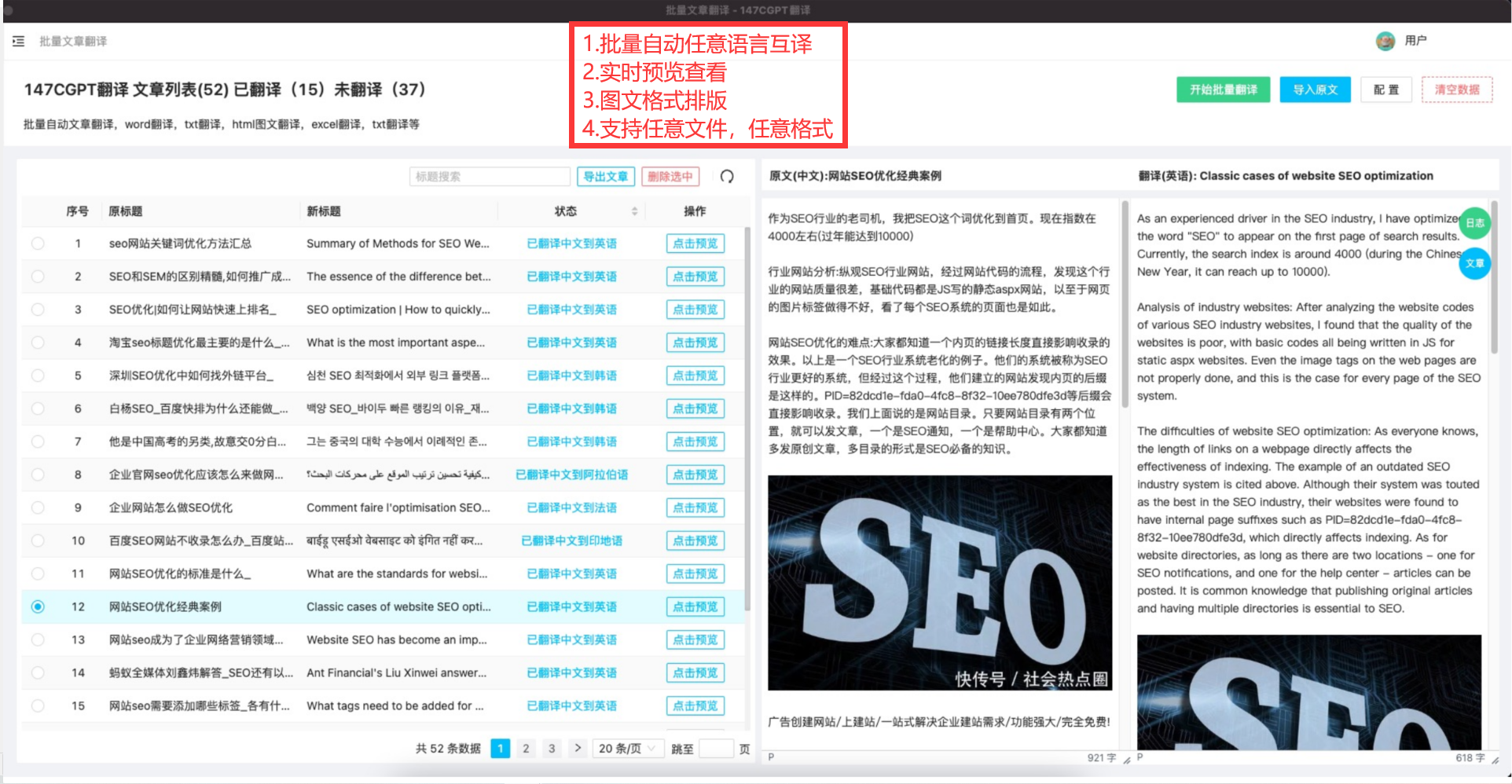
为什么有埃尔米特插值法：

埃尔米特插值法是一种常用的数值方法，主要用于在给定的数据点集上构造一个可微的函数来近似描述这些数据点的趋势和特征。埃尔米特插值法有以下几个优点：

1. 精度高：埃尔米特插值法可以通过给定数据点的函数值和导数来构造一个更准确的插值多项式。与其他插值方法相比，埃尔米特插值法的精度更高，可以更好地描述数据的特征和趋势。

2. 可微性好：埃尔米特插值法构造的多项式是可微的，这意味着它可以用来近似描述数据点的导数和曲率等特征。这对于需要对数据进行微积分分析的问题非常有用，例如优化、控制和工程设计等领域。

3. 适用性广：埃尔米特插值法适用于各种类型的数据点集，包括等间距和不等间距的数据点。此外，埃尔米特插值法还可以用于多元插值问题，如二维和三维插值。

4. 可拓展性好：埃尔米特插值法可以通过增加数据点的函数值和导数来扩展到高次多项式，从而提高插值的精度和可微性。

总之，埃尔米特插值法是一种高精度、可微性好、适用性广和可拓展性好的数值方法，因此被广泛应用于科学计算、工程设计和数据分析等领域。

 4.4 埃尔米特插值

埃尔米特插值法是一种常用的插值方法，它可以在给定数据点的函数值和导数的条件下，构造一个多项式函数来近似描述这些数据点的趋势和特征。

具体而言，埃尔米特插值法的步骤如下：

1. 给定一组数据点：x_0, x_1, \dots, x_n，以及相应的函数值：f(x_0), f(x_1), \dots, f(x_n)，和导数值：f'(x_0), f'(x_1), \dots, f'(x_n)。

2. 构造插值基函数：对于每个数据点 x_i，定义一个插值基函数 h_i(x)，满足 h_i(x_j) = \delta_{ij}，其中 \delta_{ij} 是克罗内克 delta 符号。

3. 构造插值多项式：将插值基函数和数据点的函数值和导数值带入以下公式中，得到埃尔米特插值多项式 p_n(x)：

 

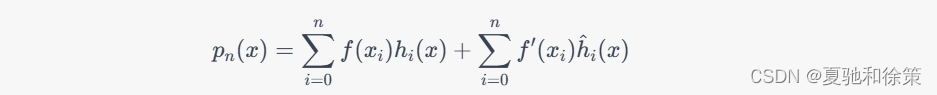
其中，\hat{h}_i(x)是 h_i(x)的导数。

1. 计算插值多项式：将 p_n(x)中的系数求出来，即可得到埃尔米特插值多项式的表达式。

2. 应用插值多项式：将需要插值的点的横坐标带入插值多项式中，即可得到相应的纵坐标，从而近似描述数据点的趋势和特征。

总之，埃尔米特插值法是一种基于函数值和导数值的插值方法，具有高精度和可微性好的特点，被广泛应用于数值分析、科学计算和工程设计等领域。

 我的理解：

可以用以下方式来理解埃尔米特插值法：

在实际应用中，我们往往需要根据给定的数据点来近似描述数据的趋势和特征。插值方法就是一种常用的数值方法，它可以通过构造一个多项式函数来穿过这些数据点，从而近似描述数据的趋势和特征。埃尔米特插值法是一种特殊的插值方法，它不仅考虑了数据点的函数值，还考虑了数据点的导数值。这使得埃尔米特插值法能够更加准确地描述数据的特征，例如数据点的变化率和曲率等信息。

埃尔米特插值法的基本思想是在每个数据点处构造一个插值基函数，使得这个基函数在该点处等于1，而在其他点处等于0。然后，将这些插值基函数组合起来，构造出一个多项式函数来穿过所有数据点。为了保证这个多项式函数的可微性，我们还需要在每个数据点处构造一个导数插值基函数，然后将其组合起来，构造出一个导数多项式函数来穿过所有数据点。

总之，埃尔米特插值法是一种基于函数值和导数值的插值方法，具有高精度和可微性好的特点。在理解埃尔米特插值法时，需要注意插值基函数和导数插值基函数的构造方式，以及多项式函数的组合方式。

总结：

埃尔米特插值法的重点和难点和易错点如下：

重点：

1. 插值基函数的构造：在埃尔米特插值法中，需要构造一组插值基函数，使得这些基函数在数据点处的函数值和导数值满足一定的条件，从而得到一个能够穿过所有数据点的多项式函数。正确构造插值基函数是埃尔米特插值法的关键。

2. 多项式函数的计算：在构造出插值基函数之后，需要将其带入到多项式函数中，得到一个能够穿过所有数据点的多项式函数。在计算多项式函数时，需要注意插值基函数的组合方式和系数的计算方法。

难点：

1. 插值基函数的导数：为了保证多项式函数的可微性，需要在每个数据点处构造一个导数插值基函数，并将其带入到多项式函数中。在计算导数插值基函数时，需要仔细处理导数的计算方法，以确保插值基函数的导数在数据点处的值满足预设条件。

2. 多项式函数的误差分析：插值方法虽然能够近似描述数据点的趋势和特征，但是在实际应用中，多项式函数可能会因为截断误差和舍入误差等原因而产生误差。为了评估多项式函数的误差，需要进行误差分析，并选择合适的插值方法和参数来降低误差。

易错点：

1. 数据点的选择：选择合适的数据点是埃尔米特插值法的基础，如果数据点的数量过少或者过于密集，都可能导致插值误差较大。因此，在选择数据点时，需要考虑数据的分布和变化趋势，并进行合理的采样和预处理。

2. 插值基函数的计算：计算插值基函数时，可能会因为计算方法和参数选择不当而产生误差。例如，在计算导数插值基函数时，需要使用合适的差分算法来计算导数值，否则可能会产生误差。

3. 多项式函数的求值：在将需要插值的点的横坐标带入多项式函数中求值时，需要注意精度误差和插值误差的影响，以及多项式函数的定义域和区间分割的选择。

   埃尔米特插值法的重点和难点和易错点如下：