概述

回顾混淆电路的流程，一方生成加密真值表，另一方执行计算，门电路的输入通过主动发送和不经意传输索取实现，用这样的方式来达到多方计算中一些公平性。
那么是否可以让双方拥有更加对等的地位，让每个参与方都持有一部分秘密份额，都参与计算的方法呢？
假如让双方都加入计算，那么就一定得加密，不加密的话势必会导致自己的秘密份额泄漏，那么在布尔电路中单位比特应该怎么加密呢？异或！
为什么采用异或加密呢？

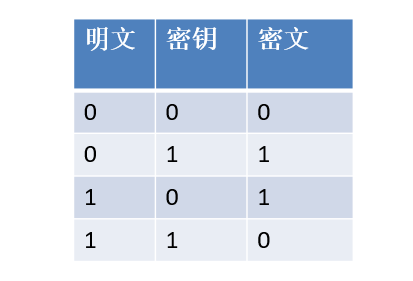
从表中可以看到，密文分布均匀，概率是相等的，而密文反推出明文的概率也是相等的，和随机猜测的概率是一样的，也就意味着只拿到密文并不能给攻击者提供任何有效的额外信息。
其次，注意到异或对于密文的计算是相当友好的。

两方GMW协议

GMW协议同时支持布尔电路和算数电路计算，这里考虑布尔电路，特点是每个参与方都持有秘密份额。

执行流程

假定参与方分为$P1$（输入为 x ∈ { 0 , 1 } n x\in \{0,1\}^n x∈{0,1}n）和$P2$输入为 y ∈ { 0 , 1 } n y\in \{0,1\}^n y∈{0,1}n，然后进行类似加法共享操作，即$P1$对于每一个输入比特 x i ∈ { 0 , 1 } x_i\in \{0,1\} xi​∈{0,1}，都随机生成一个随机比特 r i ∈ R { 0 , 1 } r_i\in_R \{0,1\} ri​∈R​{0,1}，然后发送给$P2$，此时$P1$所持有的秘密份额为$x\oplus r$，而$P2$持有的则是$r$，这样二者就共同持有$x$，相当于把$x$这个秘密做了一个加法分享，$y$也同理。
接下来考虑一个门，将输出定为$w_k$，两个输入定为$w_i$和$w_j$，然后将每个输入拆分为两部分$w_x=s_x^1\oplus s_x^2$，$P1$和$P2$分别持有两个输入的各一部分$(s_i^1,s_j^1)$和$(s_i^2,s_j^2)$

电路拆分

一般的，电路由XOR，NOT和AND三个基础门构成，下面看看如何进行安全计算（以两方为例）

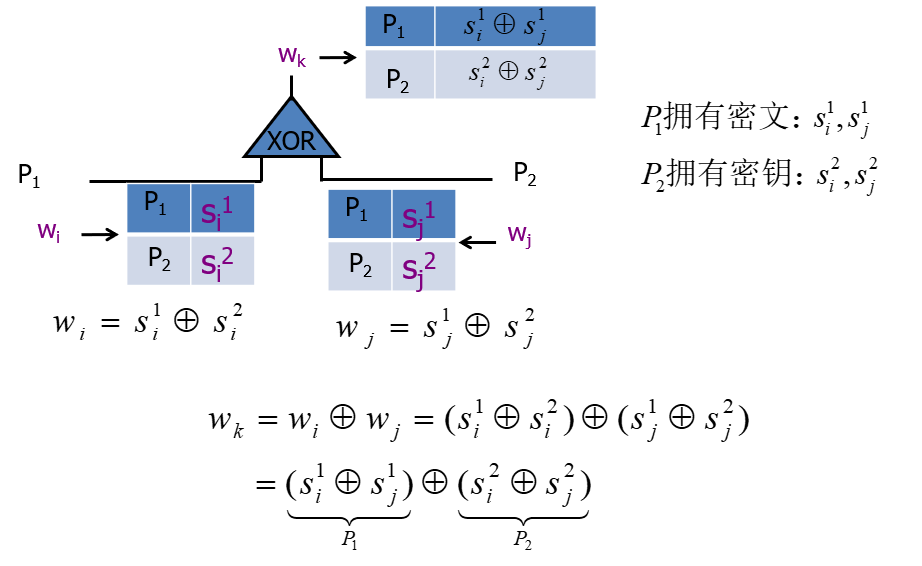
XOR

无需交互，本地计算，两方分别对自己的秘密份额进行异或即可得到结果。

NOT

无需交互，本地计算，只需各自对秘密份额取反即可

AND

显然需要交互才能进行求值。

那么应该如何安全的交互呢？
以$P1$的视角来看，它只知道自己的两份秘密份额$s_i^1,s_j^1$对应的值，而不知道$s_i^2,s_j^2$所对应的值，意味着对于未知的$(s_i^2,s_j^2)$一共有4种取值可能$(00,01,10,11)$，接着$P1$对于每一种可能都准备一份对应的秘密份额，然后执行4选1-OT协议，将对应的秘密份额发给$P2$，来获得对应的秘密份额。具体如下，
令整体的结果秘密为$S=F_{(s_i^1,s_j^1)}(s_i^2,s_j^2)=(s_i^1\oplus s_i^2)\otimes (s_j^1\oplus s_j^2)$，把这个视为输入为两个秘密份额，输出为门电路输出值的一个函数，为了不泄露自己秘密份额，$P1$选择一位随机比特 r ∈ R { 0 , 1 } r\in_R\{0,1\} r∈R​{0,1}，计算出一张4选1的OT秘密表，

随后由$P1$作为OT的发送方将OT秘密表的4行分别作为4个秘密输入，$P2$作为接收方将自己的2个秘密份额作为选择项，选择接收OT秘密表所对应的行。$P1$将$r$设置为门输出的秘密份额，$P2$则将OT协议种接收的的值作为门输出的秘密份额。这样二者就分别持有了最终结果的一部分。在计算完所有门之后，双方都公布自己拥有的所有输出秘密份额即可得到最终结果。
直观上看，很明显参与方无法得到另一个参与方输入的任何信息，$P2$只知道自己接收的OT协议的结果，而$P1$同样只知道OT协议的选择项。

多方的GMW协议

XOR和NOT门不需要交互，直接本地计算就好，所以难点在于AND门上
假如参与方为$n$个，那么和两方的类似，每个参与方都对每个输入比特都选择一个随机比特，然后发送给其他参与方，达到加法共享的效果。这样一来每个参与方都持有$（a_i,b_i）$两份输入份额。那么对AND门计算

其中部分是每个参与方可以通过自己拥有的份额计算出来的，而部分需要每个参与方两两进行一次两方的GMW即可，将得到的两部分结果进行一次XOR即可得到最终的结果。
显而易见，GC和GMW都对二进制操作很友好，GMW是以共享的角度来计算的，输入输出都各自持有一部分，后续可以继续扩展到代数级别。

参考

实用安全多方计算导论
CS 276 – Cryptography Oct 27, 2014 Lecture 16: Secure multi-party computation (GMW Protocol + Malicious Model)
Boolean Sharing（布尔共享）
【隐私计算笔谈】MPC系列专题（四）：GMW协议和BGW协议