这个专栏名为《Numpy从入门到精通》，顾名思义，是记录自己学习numpy的学习过程，也方便自己之后复盘！为深度学习的进一步学习奠定基础！希望能给大家带来帮助，爱睡觉的咋祝您生活愉快！ 这一篇介绍《Numpy从入门到精通—— Numpy运算符|批处理》

在前面几次分享中，我们学习了Numpy的矩阵生成，数据读存、获取、广播机制等，这一次我们进一步学习Numpy的算数运算符以及批处理！

一.星乘（*）

星乘也称为对应元素相乘、逐元素相乘，对应的函数为np.multiply()，输出的大小与相乘数组或者矩阵的大小一致：

• numpy.multiply(x1,x2,/,out=None,*,where=True,casting=“same_kind”,order=“k”,dtype=None,subok=True[,signature,extobj])

下面用程序进行说明：

#!/usr/bin/env python
# -*- coding: UTF-8 -*-
"""
@Project ：numpy学习 
@File    ：task_14.py
@IDE     ：PyCharm 
@Author  ：咋
@Date    ：2023/4/21 20:41 
"""
import numpy as np
A = np.array([[1, 2], [-1, 4]])
B = np.array([[2, 0], [3, 4]])
print(A * B)
#或另一种表示方法
print(np.multiply(A, B))

输出为：

[[ 2  0]
 [-3 16]]
[[ 2  0]
 [-3 16]]

可以看到，np.multiply()与*效果是一样的，numpy不仅可以对数组进行对应的元素相乘，也可以与单一的数值进行运算。运算时，numpy数组的每一个元素与标量进行运算，这也是广播机制的应用。下面通过代码进行说明：

#!/usr/bin/env python
# -*- coding: UTF-8 -*-
"""
@Project ：numpy学习 
@File    ：task_15.py
@IDE     ：PyCharm 
@Author  ：咋
@Date    ：2023/4/21 20:51 
"""
import numpy as np
A = np.array([1,2,3,4,5,6])
print(A*2.0)
print(A/2.0)

输出为下：

[ 2.  4.  6.  8. 10. 12.]
[0.5 1.  1.5 2.  2.5 3. ]

推而广之，一些激活函数也是可以基于np的广播机制特性的。

#!/usr/bin/env python
# -*- coding: UTF-8 -*-
"""
@Project ：numpy学习 
@File    ：task_16.py
@IDE     ：PyCharm 
@Author  ：咋
@Date    ：2023/4/21 20:56 
"""
import numpy as np
X = np.random.rand(2, 3)


def sigmoid(x):
    return 1 / (1 + np.exp(-x))


def relu(x):
    return np.maximum(0, x)


def softmax(x):
    return np.exp(x) / np.sum(np.exp(x))


print("输入参数X的形状：", X.shape)
print("激活函数sigmoid输出形状：", sigmoid(X).shape)
print("激活函数relu输出形状：", relu(X).shape)
print("激活函数softmax输出形状：", softmax(X).shape)

输出为：

输入参数X的形状： (2, 3)
激活函数sigmoid输出形状： (2, 3)
激活函数relu输出形状： (2, 3)
激活函数softmax输出形状： (2, 3)

二. 点乘（.）

点积运算又被称为内积运算，一般格式为：

• np.dot(a,b,None)

我们直接通过程序来看dot的具体用法：

#!/usr/bin/env python
# -*- coding: UTF-8 -*-
"""
@Project ：numpy学习 
@File    ：task_17.py
@IDE     ：PyCharm 
@Author  ：咋
@Date    ：2023/4/21 21:04 
"""
import numpy as np
X1=np.array([[1,2],[3,4]])
X2=np.array([[5,6,7],[8,9,10]])
X3=np.dot(X1,X2)
print(X3)

输出为：

[[21 24 27]
 [47 54 61]]

和线性代数计算过程是一样的，具体计算过程可以看下面这张图：

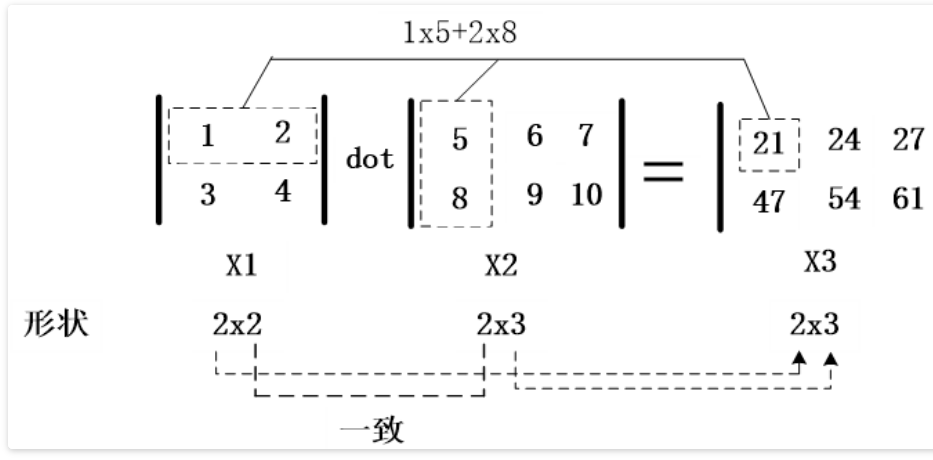
从上面这个图我们也能看出来，如果X1与X2进行点积运算，X1的第二维度与X2的第一维度要是一样的。点积运算在神经网络中的使用是非常频繁的，在神经网络中输入I与权重矩阵W之间的运算就是点积运算：

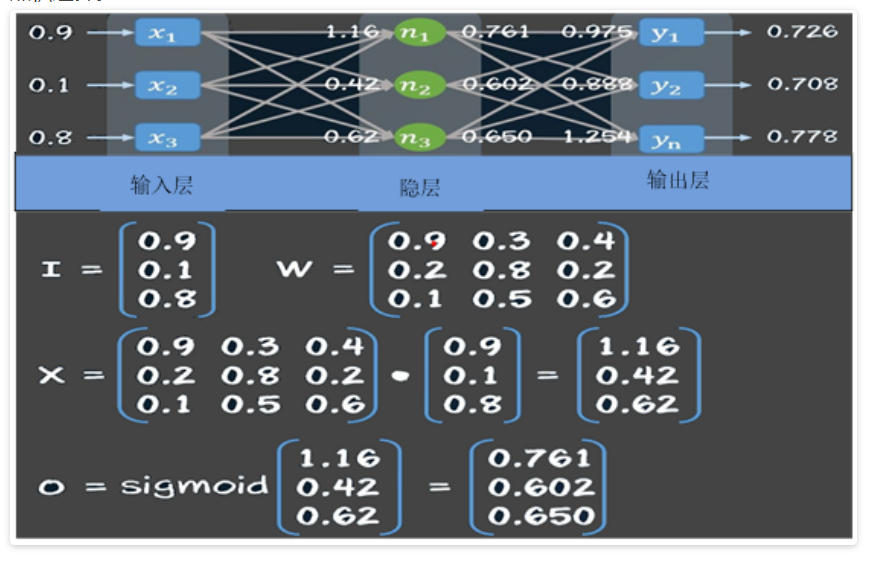
这里的sigmoid就是激活函数，对应的公式上面已经写过，这里就不再赘述。

三.批处理

数据是深度学习的基础，在深度学习中，数据量往往是比较大的。所有我们通常要采用批处理的方式，比如说随机梯度方法（SGD），就是选用一批数据求模型的损失。如何把大数据分成多个批次呢？可以采用如下步骤：

• 得到数据集
• 随机打乱数据
• 定义批大小
• 批处理数据集

我们依然是直接通过代码来进行说明：

#!/usr/bin/env python
# -*- coding: UTF-8 -*-
"""
@Project ：numpy学习 
@File    ：task_18.py
@IDE     ：PyCharm 
@Author  ：咋
@Date    ：2023/4/21 21:21 
"""
import numpy as np
#生成10000个形状为2X3的矩阵
data_train = np.random.randn(10000,2,3)
#这是一个3维矩阵，第一个维度为样本数，后两个是数据形状
print(data_train.shape)
#(10000,2,3)
#打乱这10000条数据
np.random.shuffle(data_train)
#定义批量大小
batch_size=100
#进行批处理
# print(np.sum(data_train))
# x_batch_sum =0
for i in range(0,len(data_train),batch_size):
    x_batch_sum=np.sum(data_train[i:i+batch_size])
print("第{}批次,该批次的数据之和:{}".format(i,x_batch_sum))

输出：

(10000, 2, 3)
第9900批次,该批次的数据之和:21.031025152935968

分批次输出，可以防止内存直接爆满，batch-size也是深度学习优化模型的一个重要参数！