0. 简介
最近几年IPC相关的文章也出了不少,最近作者有看到了一篇比较有意思的ICP论文—《Gravity-constrained point cloud registration》,这篇论文将传统的ICP考虑了重力因素,高频率的IMU数据弥补了低频的传感器数据。除此之外,可以从重力向量中获取三自由度姿态中的两个。在视觉里程计中,IMU已经被用来将6自由度位姿估计转换为4自由度。在lidar SLAM中,重力测量在后端优化中经常被用来作为惩罚项来防止地图变形。文中提出了一种基于迭代最近点(ICP)的前端方法,其利用了重力向量提供的旋转可观自由度,并且提供了与重力向量对齐的位姿估计。该方法相比于传统的ICP算法,可以减小30%的定位漂移。这部分代码已经在Github上开源了。这非常便于我们对此进行学习。同时作者提到具体的代码也推送给了libpointmatcher开源库。
1. ICP Mapper
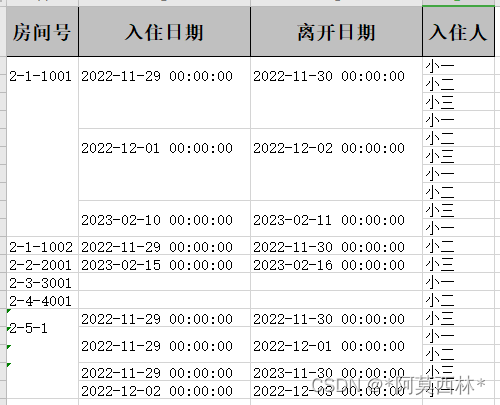
建图以及后续定位工作是使用本问开源的的norlab icp映射器实现的。这是一个轻量化的建图系统,本质上封装了ICP功能,同时执行输入激光雷达数据过滤和点云图内存管理。在我们的设置中没有执行全局优化,点云图随着机器人在环境中导航而增量增长。mapper执行以下步骤:
1)根据初始姿态估计
T
˘
\breve{T}
T˘将输入激光雷达扫描图像转换为世界帧
2)使用ICP将扫描图像注册到地图上
3)将扫描图像插入到地图内部
初始估计
T
˘
\breve{T}
T˘是由基于机器人里程计的平移向量和基于IMU的方向四元数组成。输入激光雷达扫描通过随机下采样的方式来保持移动机器人对激光点云数据处理的实时性能。输入激光数据的机器人运动失真矫正则也是根据里程计和IMU数据来完成的。最后,只需要将对齐的扫描点的一个子集合并到地图中即可完成建图。

2. 4-DOF ICP
ICP算法旨在评估一个刚性变换 T ˘ \breve{T} T˘来将最好将一组3d点 Q \mathcal{Q} Q(即地图点云)与第二组3d点 P \mathcal{P} P(即扫描点云),通过最小化误差函数 e \mathcal{e} e:
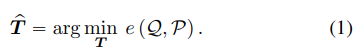
在我们的方法中,我们选择将点到面的误差定义为
e
\mathcal{e}
e[19],因为它在大多数情况下优于点到点定义[9]。然而,4-DOF的修正可以隐式扩展到点到高斯误差定义,因为后者可以转换为点到平面,如Babin 这篇文章[20]所示。我们首先将变换参数
T
T
T定义为一个4D向量
τ
\mathcal{τ}
τ:
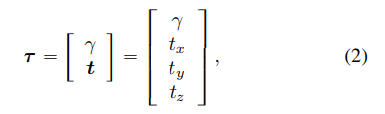
其中
γ
γ
γ是沿
z
z
z轴的旋转分量,
t
x
,
t
y
t_x, t_y
tx,ty和
t
z
t_z
tz是平动分量。与
e
\mathcal{e}
e的经典6自由度定义相比,
τ
\mathcal{τ}
τ遗漏了沿x轴和y轴的旋转分量。然后,我们遵循点到平面误差函数的标准定义
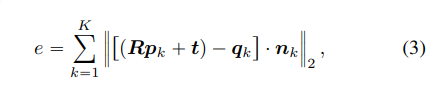
其中
n
k
n_k
nk是表示在点
q
k
q_k
qk处曲面的法向量,
R
=
R
(
γ
)
\mathbf{R}=R(γ)
R=R(γ)是一个旋转矩阵,指数
k
k
k表示来自
Q
\mathcal{Q}
Q和
P
\mathcal{P}
P的成对点,密切遵循Pomerleau[21]的最小化推导,但修改为4自由度,旋转矩阵
R
\mathbf{R}
R仅执行偏航旋转。另外两个旋转是不需要的,因为
P
\mathcal{P}
P点云已经根据最初的
T
˘
\breve{T}
T˘姿态估计被映射器预对齐。最小化方法依赖于旋转矩阵线性化。这种线性化可以使用小角度近似来实现:
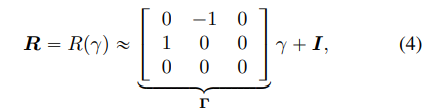
I
\mathbf{I}
I是单位矩阵。在ICP环境下,通过整个配准算法的迭代过程,降低了线性化的影响。结合(3)和(4),我们可以将目标函数近似为
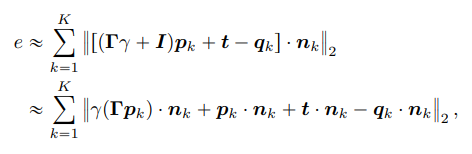
用标量三重积和重新组织这些项,其中n_k是点q_k所在的平面。将上述的R代入到误差中,可以写成这样
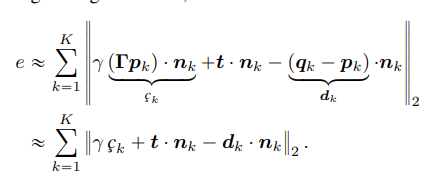
然后我们可以最小化误差
e
\mathcal{e}
e关于
r
\mathbf{r}
r和
t
\mathbf{t}
t,并使偏导为零
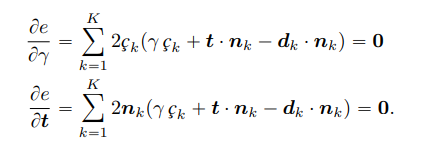
我们可以把这些导数组合成线性形式
A
τ
=
b
\mathbf{A}τ = \mathbf{b}
Aτ=b,把自变量放在方程右边