122.买卖股票的最佳时机II

遇到每天正利润就收集，负利润就不收集

• 链接:代码随想录

• 解题思路：
  ①因为可以多次买卖，所以考虑到最终把最终利润进行分解
  如假如第0天买入，第3天卖出，那么利润为：prices[3] - prices[0]。相当于(prices[3] - prices[2]) +
  (prices[2] - prices[1]) + (prices[1] - prices[0])。
  此时就是把利润分解为每天为单位的维度，而不是从0天到第3天整体去考虑！
  ②贪心所贪的地方：只收集每天卖出收集的正利润，不需要记录区间
  ③局部最优：收集每天的正利润，全局最优：求得最大利润。

• 

public int maxProfit(int[] prices) {
    int result = 0;

    for (int i = 1; i < prices.length; i++) {
        //只要每一天的正利润
        result += Math.max(prices[i] - prices[i - 1], 0);
    }

    return result;
}

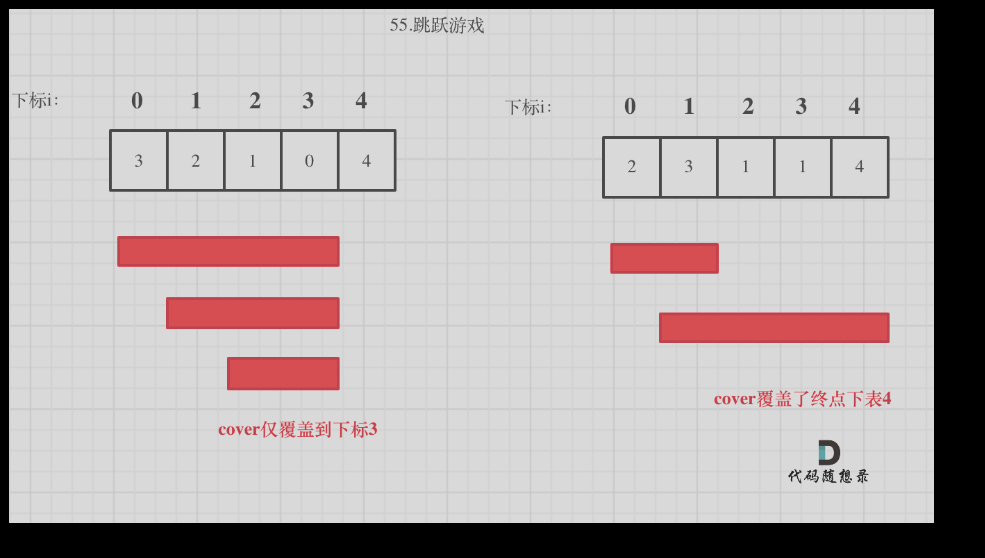
55. 跳跃游戏

• 链接:代码随想录

关键点：解决的不是每次跳几步，而是跳跃最大覆盖范围

• 解题思路：

  1. 不用考虑每次跳几步，就每次更新最大的跳跃范围即可

  2. 贪心算法局部最优解：每次取最大跳跃步数（取最大覆盖范围），整体最优解：最后得到整体最大覆盖范围，看是否能到终点。

  3. 理解cover为最大覆盖位置的下标，这样只需遍历每个元素，确定最大覆盖位置能不能到最后一个为止即可

• 

public boolean canJump(int[] nums) {

    int cover = 0;//定义最大覆盖的下标

    for (int i = 0; i <= cover; i++) {//这里i表示能走到的最大范围
        cover = Math.max(i + nums[i], cover);//这里注意覆盖范围，不用让cover做减法操作，cover表示最大能走到的位置

        if(cover >= nums.length - 1){
            return true;
        }
    }

    return false;
}

//超时解法
public boolean canJump(int[] nums) {

    for (int i = nums.length - 2; i >= 0;i--) {
        if(nums[i] == 0){
            int j = i - 1;
            while(j >= 0){
                if(i - j > nums[j]){
                    return false;
                }
            }
        }
    }

    return true;
}

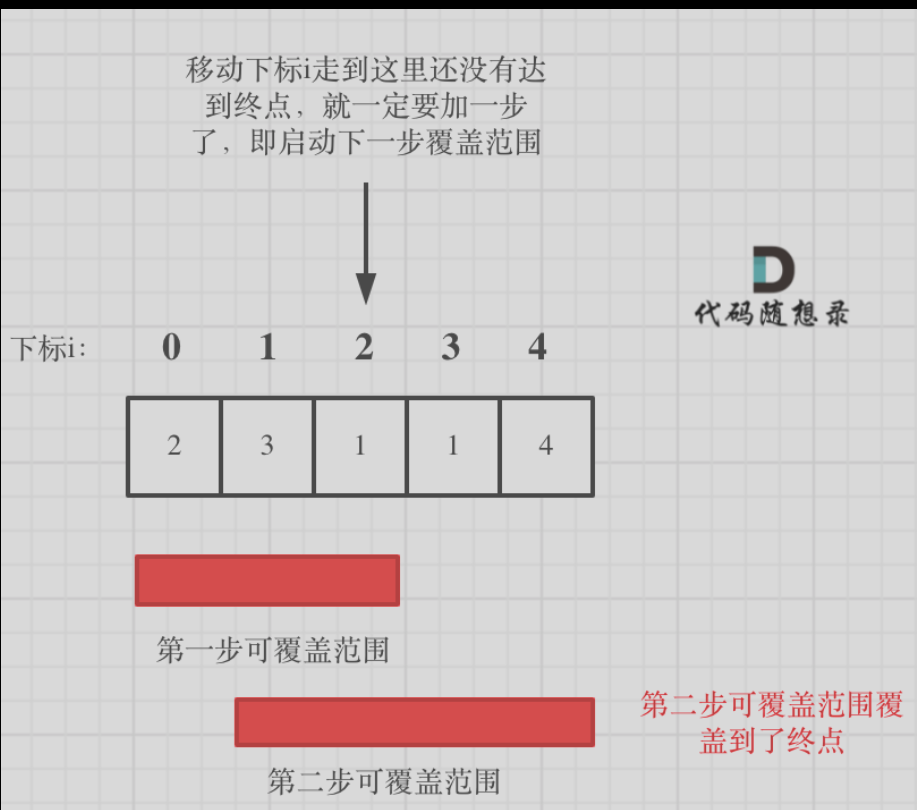
45.跳跃游戏II⭐️

• 题目链接:代码随想录

局部最优：要以最少的步数换取最大的范围

• 解题思路：

   1.解题的时候**始终从最小步数开始走**，要不断地更新能跳到的最大范围
   2.要从覆盖范围出发，不管怎么跳，覆盖范围内一定是可以跳到的，以最小的步数增加覆盖范围，覆盖范围一旦覆盖了终点，得到的就是最小步数！
  
   3.这里需要统计两个覆盖范围，当前这一步的最大覆盖和下一步最大覆盖。  当前这一步的最大覆盖是为了检测当前步数的最大水平，而下一步最大覆盖是为了检测下一步的能力
  
  4.这里步数要一步一步向后走，这样才能全部统计走过的每一步的最大范围
  

• 

public int jump(int[] nums) {
    //特殊情况
    if(nums.length == 0){
        return 0;
    }

    int res = 0;
    int curCover = 0;//当前最大覆盖范围
    int nextCover = 0;//下一步最大覆盖范围

    for (int i = 0; i < nums.length; i++) {//一次遍历，不断更新最大范围
        nextCover = Math.max(i + nums[i],nextCover);//记录每个状态的最大范围

        if(i == curCover){

            //还没到最后一个位置
            if(i < nums.length - 1){

                curCover = nextCover;//更新最大范围
                res++;//再走一步
                //如果下一步覆盖范围能覆盖最后一个，那么直接返回即可
                if(nextCover >= nums.length - 1){
                    break;
                }
            }else{
                break;
            }
        }

    }

    return res;
}