一.划分区间的选取

目前市面上常用的有两种划分区间，一种是hoare划分另一种是Lomuto划分。常见快速排序实现模版比如挖坑法和经典快速排序就是用的是hoare划分。那么这两种区间划分方式有什么不同呢。先上结论，hoare划分在面对大量重复数据的时候效率会明显好于lomuto划分。当面对大量不同数据的时候两种划分区间相差不大。

下面来解释为什么大量重复数据处理效率会有差异。因为lomuto的工作流程是先选定key值，再在数组的一侧初始化两个指针i和j。遍历数组并在 arr[j] <= 枢轴时递增 i，并将 arr[i] 与 arr[j] 交换，否则仅递增 j。从循环出来后，将 arr[i] 与 key值交换。本质上就是把所有大于key值的数放在j左侧并逐渐向数组尾部滚动，按照这个工作流程在遇到大量重复数据的时候，每一个重复数据都要发生一次交换。这就会导致效率的降低。而hoare划分指针在数组两侧且在当前值等于等于key值的时候不发生交换。这样效率的差异就主要体现在交换上。详细的数学证明可以看这篇文章划分区间选取数学分析

二.代码实现lomuto版本快速排序

//lomotu划分法，和hoare划分相比没有什么优势，特点是好写，在遇到大量重复数据的时候会发生大量交换，这种情况下不入hoare
void lomotu_soart(int left,int right)//取作左边为基准点，外网大多数取右边为基准点
{
	if (left >= right)
	{
		return;
	}
	int prev = left;
	int cur = left + 1;
	int key = left;
	while (cur <= right)   //个人认为有点像滑动窗口
	{
		if (n[cur] < n[key])  //可以优化若是prev和cur是挨着的就不用交换，因为此时他俩之间并没有大于基准值的值不用考虑交换
		{						//这里带不带等于都可以，因为和基准值相同的值是挨着的且没有先后可言
			prev++;		//要先自增在交换才能把第一个大于基准值的值换到右边
			swap(n[prev], n[cur]);
		}
		cur++;
	}
	swap(n[prev], n[key]); //最后把prev指针的值和key值交换，因为prev当前指向的值小于key,prev后面的值大于key
	lomotu_soart(left,prev-1);
	lomotu_soart(prev+1,right);
}

三.hoare版本快速排序

两种实现方法

传统方法：

//非竞赛用，传统方法，跟上面的挖坑法一样无法处理大量重复的数据
void tradition(int start,int end)   //细节处理和挖坑法是一样的
{
	if (start >= end)
	{
		return;
	}
	int left = start, right = end;		//交换的原因和挖坑法一样
	int pos = (left + right) / 2;
	int key = n[pos];
	swap(n[pos], n[left]);
	pos = start;

	while (left < right)
	{										  
		while (left < right && n[right] >= key) //因为忽略了key值，也就是key值卡不住指针遍历的范围，所以需要加上范围的控制。
//（若是不忽略key值本身是可以控制住遍历范围的，一共就两种情况，有比key值小的和没有比key值小的，有比key值大的情况下当前指针至少停下来两次，没有的话至少停下来一次。这样就能确保至少停下来一次
//同时不用考虑左右指针错过的问题，当左右指针相遇时由于是后置自增会先判断后自增。且左右指针相遇意味着左右指针两侧已经满足当前指针侧的判断条件，
//这也就意味着不满足另一侧指针的判断条件，也就必定会跳出循环）
		{
			right--;
		}
		while (left < right && n[left] <= key)//这里和上面的情况一样
		{
			left++;
		}
		swap(n[left], n[right]);
	}
	swap(n[pos], n[left]);//这里left还是right都可以。
	tradition(start, left-1);
	tradition(left+1, end);
	return;
}

挖坑法

//非竞赛用，若时间要求高则会在处理大量重复数据的时候超时,但易于理解  (和传统方法比减少了拷贝，但本质没有什么区别)
void dig_hole( int start, int end) //采用hoare区间划分的挖坑法，本质和传统快排思路基本一致
{
	if (start >= end)
	{
		return;
	}
	int left = start, right = end, hole = (left + right) / 2;//这里可以取直接取左第一个值或者右第一个值作为坑，这里用数组中间的值作为坑，
	int key = n[hole];										//这样能部分降低对有序数组排序时效率退化为n方的问题（最好用三数取中）
	swap(n[left], n[hole]);       //解释一下为什么要把取到的值交换到第一个位置，因为要确保两个指针遍历所有元素，这样才能找到所有小于和大于基值的值
	hole = left;					//要是不交换的话还有可能出现的问题就是当指针遍历到坑的位置的时候会再次判断坑的值，但此时坑的值不应该在这里判断
	while (left < right)
	{										  //里层循环有两点需要注意
											  //不光要在外层控制left小于right,还要在内层判断，因为我们判断等于基准值的时候也是会继续向后走的，这样就有可能越界
											  //当基准值在左侧的时候要先遍历右侧，因为我们需要保证最后的指针指向的值在退出循环时永远小于等于基准值（这个条件需要通过右指针来限制，因为右指针停留的值一定是小与等于基准值的），
		while (left < right && n[right] >= key)//右边先走意味着最后一步一定是左，此时右指针指向一定是小于等于基准值的，当左指针撞上右指针的时候一定是小与等于基准值的
		{
			right--;
		}
		n[hole] = n[right];
		hole = right;
		while (left < right && n[left] <= key)
		{
			left++;
		}
		n[hole] = n[left];
		hole = left;
	}
	n[hole] = key;
	dig_hole(start, hole - 1);
	dig_hole(hole+1, end);
	return;
}

挖坑法比传统方法稍微好一点因为挖坑法交换用的少赋值用得多，他把交换的过程变成了左右反复填坑的过程。这样就能减少部分交换提升一点效率。但是这样的话原先的一次交换就需要两次赋才能实现。我个人认为差不多。

四.竞赛模板的选取

上文这两种hoare方法都不适合作为竞赛模板使用，虽然要比lomuto方法好很多但在处理大量重复数据的时候还是有二叉树退化效率降低的问题。

假设我们有以下情况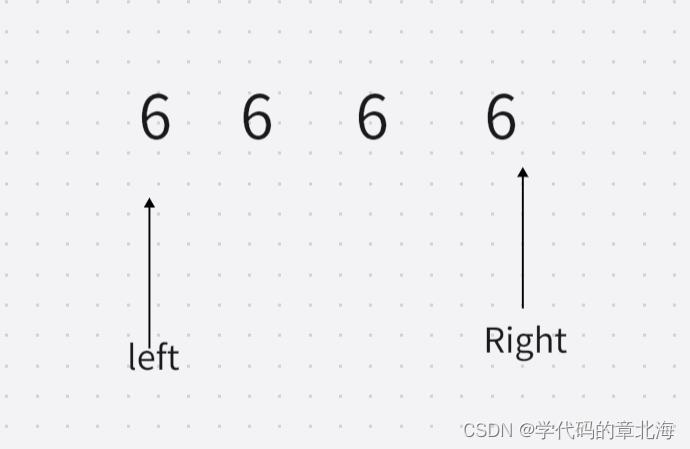

当我们用传统方法的时候，假设先动右指针，由于所有数据相同，就会变成这种情况

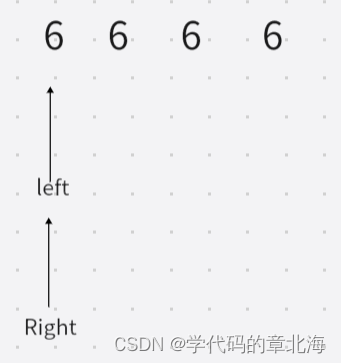
这时进行分治处理的话处理的就是后面的三个六，这个过程依次进行意味着要依次处理n-1,n-2,n-3...个数据这就会导致二叉树的退化。挖坑法由于和传统方法没有太大区别，都会勉励这个问题，哪怕是加上三数取中也解决不了这个问题，因为你必定要把key值交换到头或者尾。用三路划分可以解决这个问题，不过个人认为有点把这个问题复杂化了。接下来介绍竞赛模板。

五.竞赛模板的代码实现

这段代码本质也是hoare划分，不过有上文可以知道，之前的两个写法每次将一个值摆在正确的位置。当重复数据多的时候就会造成大量重复数据堆在一起，就有可能在分治的时候把所有的相同的值分在同一侧，也就是上面画的情况。我们可以通过将相同的值平均的分配在分治的两侧来解决这个问题。也就是每一趟不把key值放在精确的位置就可以。如果想证明这种循环分治的正确性可以看这篇文章分析循环式的正确性和细节分析

细节处理：

由于我们不需要把key值摆放到精确位置，只需要分成两个部分一部分<key值，一部分大于key值就可以。这样在判断循环的时候就可以不忽略等于key值的值了，这就意味着可以用key值来限制左右指针遍历的范围了。（具体如何限制的可以参考上文hoare排序中的注释），也就说明可以不用在遍历单个指针的时候加上范围控制了。
循环式的正确性分析，由于最后一轮的if语句一定不执行，所以只能保证:q[left..i-1] <= x, q[i] >= x和q[r+1..right] >= x, q[r] <= x。
由q[l..i-1] <= x，i >= r和 q[r] <= x 可以得到 q[l..r] <= x和q[r+1..right] >= x，这时i-1的位置也是r的位置，r+1的位置也是i的位置。
总结就是q[l..r] <= x,q[r+1..right] >= x。或者q[l,i-1]<=x,q[i,right] >= x.
由于不需要把key值摆放到正确位置，所以在选择左侧第一个值的时候就不需要先遍历右侧的指针了。右侧也是同理。
必须要用先判断后自增，因为我们在遇到等于key值的时候是会跳出循环等待交换的。如果我们先判断后自增，在左右指针都指向等与key值的时候就会反复跳出循环，但是由于下一次进入的还是这个值就会死循环。所以可以用dowhile结构先自增在判断，这样在遇到这种情况的时候就在进行第二次循环的时候就会先自增就避免这种情况。
由于我们使用的是dowhile 结构，同时我们跳出的判断条件是 i<j,这说明在我们执行完最后一喜欢循环后，i和j可能会存在两种状态，i==j或者i>j，这点会对后面的分治划分产生影响。
由于我们已经知道了在最后i>=j，我们有两种划分方法，一种是用i，一种是用j。不论i是大于j还是等j都满足的条件是，i的左侧满足一种条件，j的右侧满足一种条件。这样就能用上面2里说明的划分区间。
由于我们采取的分治区间不一样。这时候key值的取值就会和二分查找一样出现边界问题。因为我们划分的时候不能分成0和n这就会导致无限递归。在采取[l..r] [r+1..right] 这种情况的时候，由于划分的区间已经向上取整了，为了不无限递归我们的key值要向下取证，也就是可以取left。反之用i的划分区间的时候，要用向上取整。

//竞赛用，本质还是hoare分割法，但优点是会将重复数据随机分配到左右两侧从而减少递归的深度，而之前的方法会将重复数据放到一侧，会导致二叉树退化（效率最高最优雅）
//建议当模板记忆

void best_sort(int left,int right)  //跟上面最大的区别是上面每次会将一个元素放到正确的位置上，而这种写法是每次保证左右两个区域左区域小于key值，右区域大于key值
{									//而等于key值的在左右都可以。
	if (left >= right)
	{
		return;
	}
	int l = left-1,r = right+1,key = n[left];  //暂时不优化因为这里取值和二分查找一样有边界问题。优化可以用三数取中，或者直接取中间值
	while (l < r)
	{
		do 
		{
			l++;
		} while (n[l] < key);  //不能带等于，如果带上等于在遇到两个相同数字的时候就会死循环
		do
		{
			r--;
		}while(n[r]>key);
		if (l < r)
		{
			swap(n[l],n[r]);
		}
	}
	best_sort(left,r);
	best_sort(r+1,right);
}

个人而言这是用于竞赛的最好模板，简单好写高效。