文章目录
- 332.重新安排行程:star:
- 回溯总结:star:
- 1.组合问题
- 2.切割问题
- 3.子集问题
- 4.排列问题
- 5.棋盘问题(未完待续)
- 6.复杂度分析
332.重新安排行程⭐️
- 链接:代码随想录
本题是一道困难题,其实困难点也就在容器的选择和使用上
- 结果集采用数组存取即可
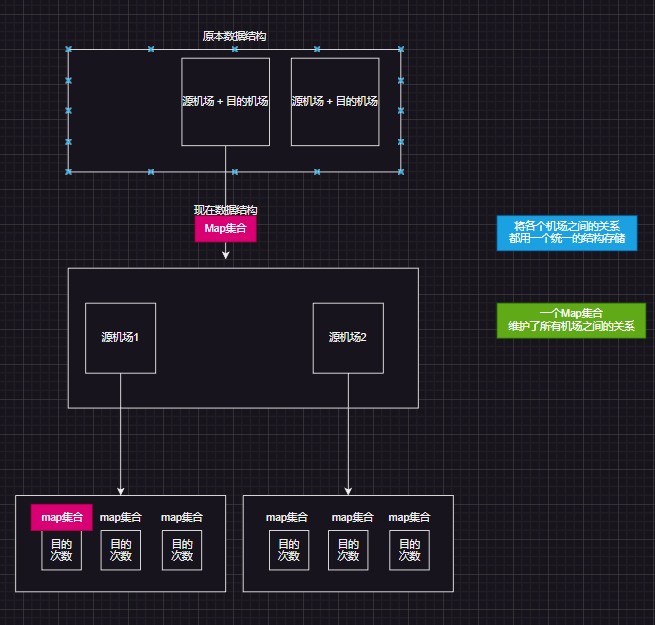
- 操作集要用一个map集合存储,Map<出发机场,Map<目的机场,目的机场所用次数>>,将两个数据关联起来要选取Map集合
-
关键点:
- 回溯法返回值:返回boolean值,目的为只需要找到一个行程,就是在树形结构中唯一的一条通向叶子节点的路线,所以找到了这个叶子节点了直接返回,有返回值可以根据底层传上来的值在当前节点做出判断和抉择。
- 接收值:一个res数组集合即可,因为只需要收集一条路径
-
解题思路:
①主函数方面:一个Map集合中维护了源机场和目的机场之间的关系,目的机场信息又维持了一个map集合,记录相关信息
②回溯函数方面:
1. 返回值:返回boolean值,为了剪枝,因为只需要一条最佳路径即可
2.终止条件,当tickets.size() + 1 即要经过的所有机场数 等于 res.size(沿途所经过的所有机场数)
3.处理逻辑:
①一定要先判断res中的最后一个值有没有包含在大map集合中,如果没有直接返回false,终止这一层遍历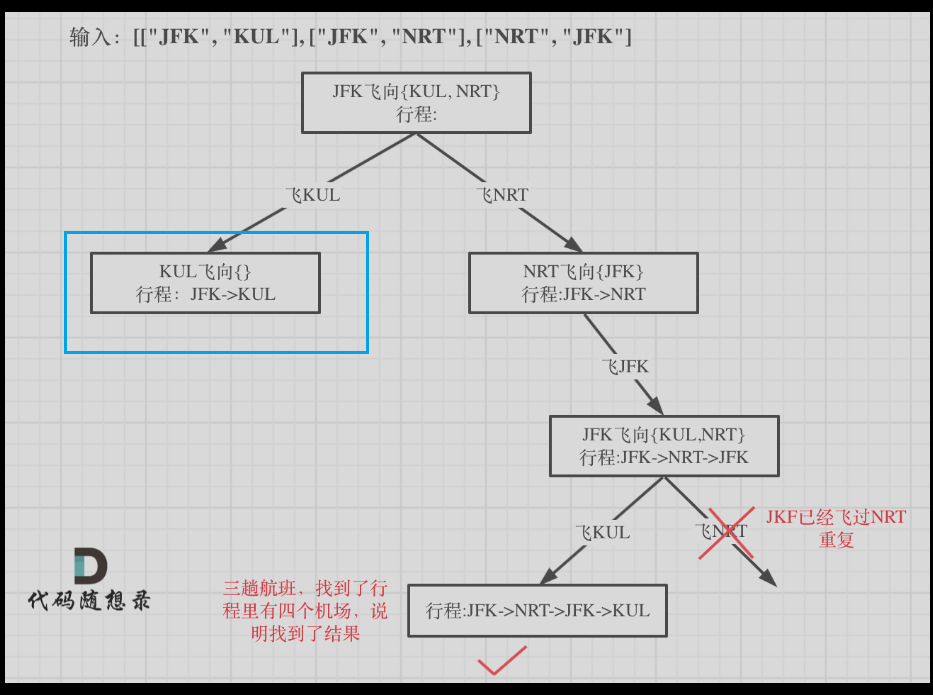
②如果map中存在源机场信息,那么接下来要做的就是从维护的目的机场map中挑选一个排序靠前的机场(TreeMap已实现)
进行加入,然后递归下一层的机场(如果返回true,说明路径可选,直接一层层归回去结束) -
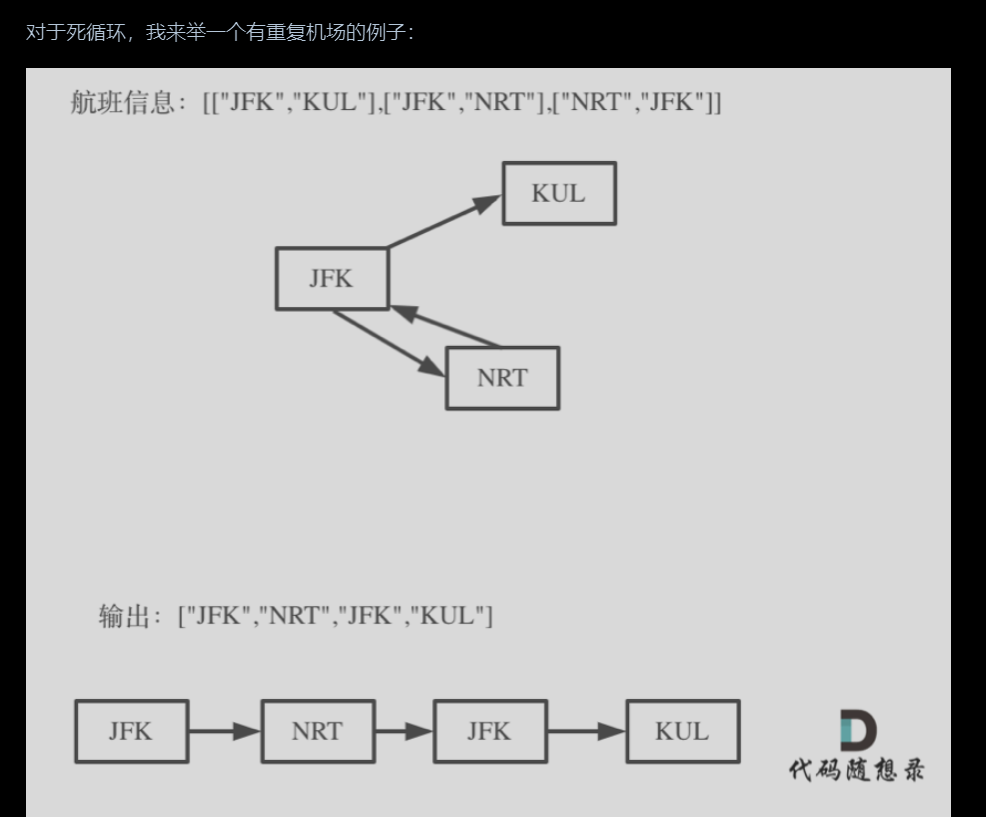
图像理解:

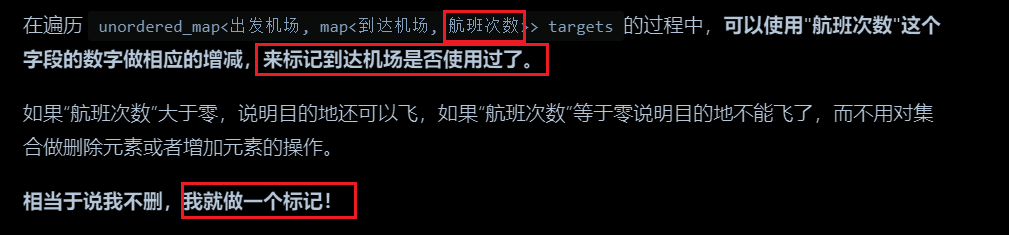
1.用处理次数来解决
2.用一个TreeMap集合来存储目的机场,遍历的时候先遍历排序靠前的
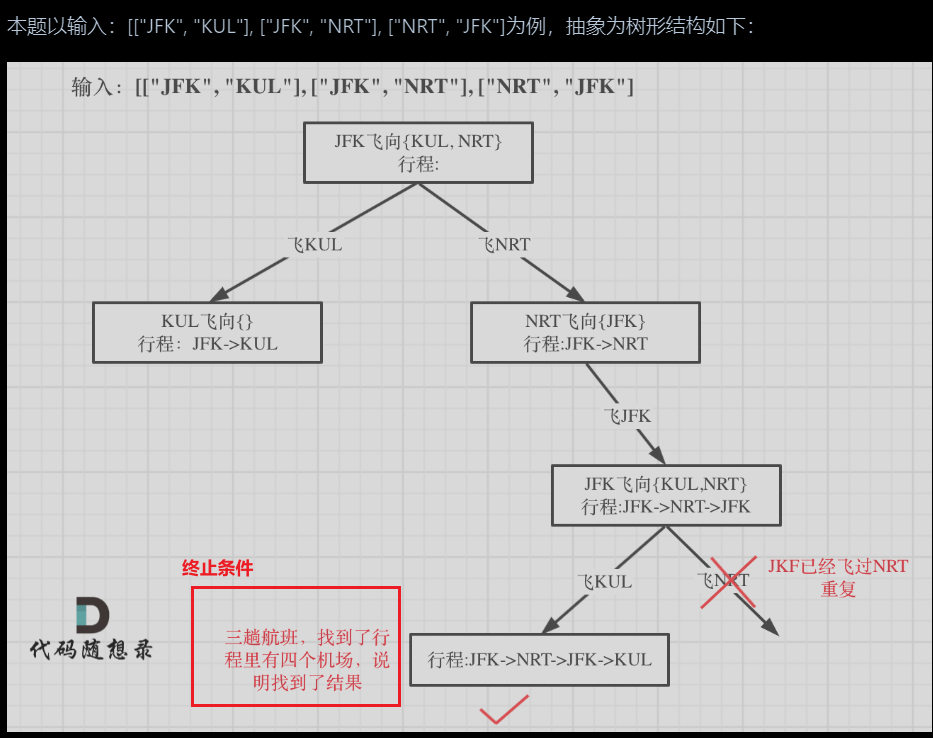
3.如果结果集中机场个数大于目标值返回
4.采用回溯遍历
public class Solution {
private LinkedList<String> res = new LinkedList<>();
private Map<String,Map<String,Integer>> map = new HashMap<>();//用来存放一个机场飞往下一个机场的航班和次数
public List<String> findItinerary(List<List<String>> tickets) {
//处理数据,放入map集合中存储每个机场飞往下一个机场的航班信息
for(List<String> ticket : tickets){
Map<String,Integer> temp;//用来添加下一班机场的名字和次数
if(map.containsKey(ticket.get(0))){//存在当前机场
//进行获取map中key为ticket的值
temp = map.get(ticket.get(0));
//先把目的机场放进去,再判断如果temp中有string,则按默认value放 + 1;否则按0 + 1
temp.put(ticket.get(1), temp.getOrDefault(ticket.get(1), 0) + 1);
//放入temp值
map.put(ticket.get(0), temp);
}else{
temp = new TreeMap();//建立一棵排好序的树
temp.put(ticket.get(1), 1);
map.put(ticket.get(0), temp);
}
}
res.add("JFK");
backtracking(tickets.size());
return new ArrayList<>(res);
}
private boolean backtracking(int ticketNum) {
//终止条件
if(res.size() == ticketNum + 1){
return true;//检测到true才直接往上放回
}
String last = res.getLast();
if(map.containsKey(last)){//防止出现null的情况
//进入处理逻辑,这里面的target已经按顺序排好,因为是target存储在TreeMap集合中
for(Map.Entry<String,Integer> target : map.get(last).entrySet()){
int count = target.getValue();
if(count > 0){//每个字符串数组只能用一次
res.add(target.getKey());
target.setValue(count - 1);
//回溯过程,如果传过来的数据为true,直接返回递归的一条分支,不再回溯和for循环
if(backtracking(ticketNum)){
return true;
}
//回溯
res.removeLast();
target.setValue(count);
}
}
}
//用来表示这一分支的最终结果
return false;
}
}
回溯总结⭐️
- 题目链接:代码随想录
回溯是递归的副产品,只要有递归就会有回溯
-
整体题目:

-
for循环遍历的时候什么时候加上startIndex?
-
组合问题:
如果是一个集合来求组合的话,就需要startIndex,如求一个组合和的问题
如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex,如求多组电话号码和的问题
-
1.组合问题
-
- 求解
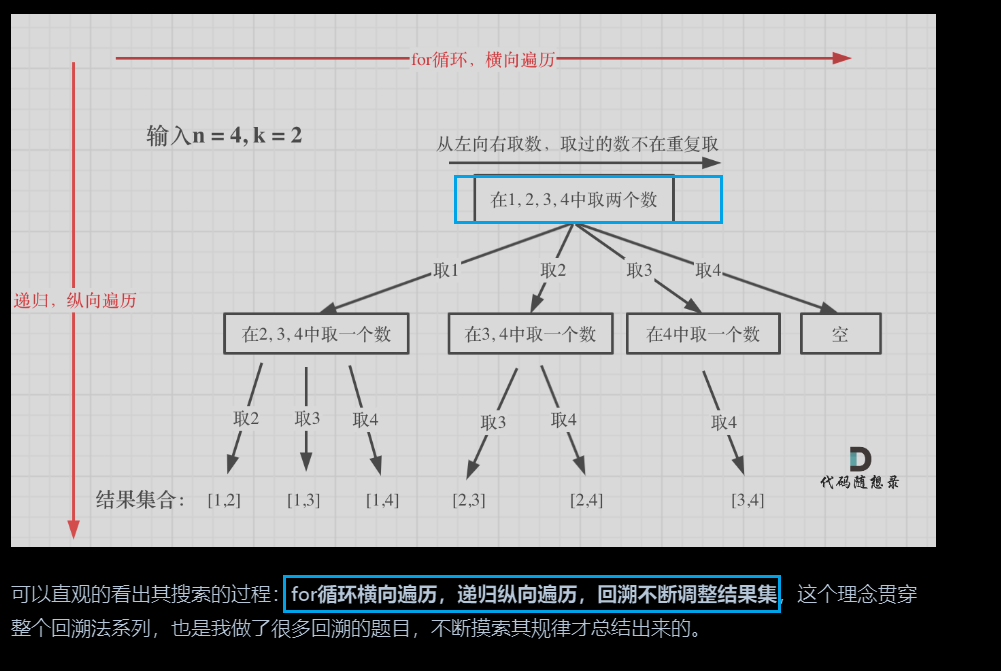
2. 剪枝:
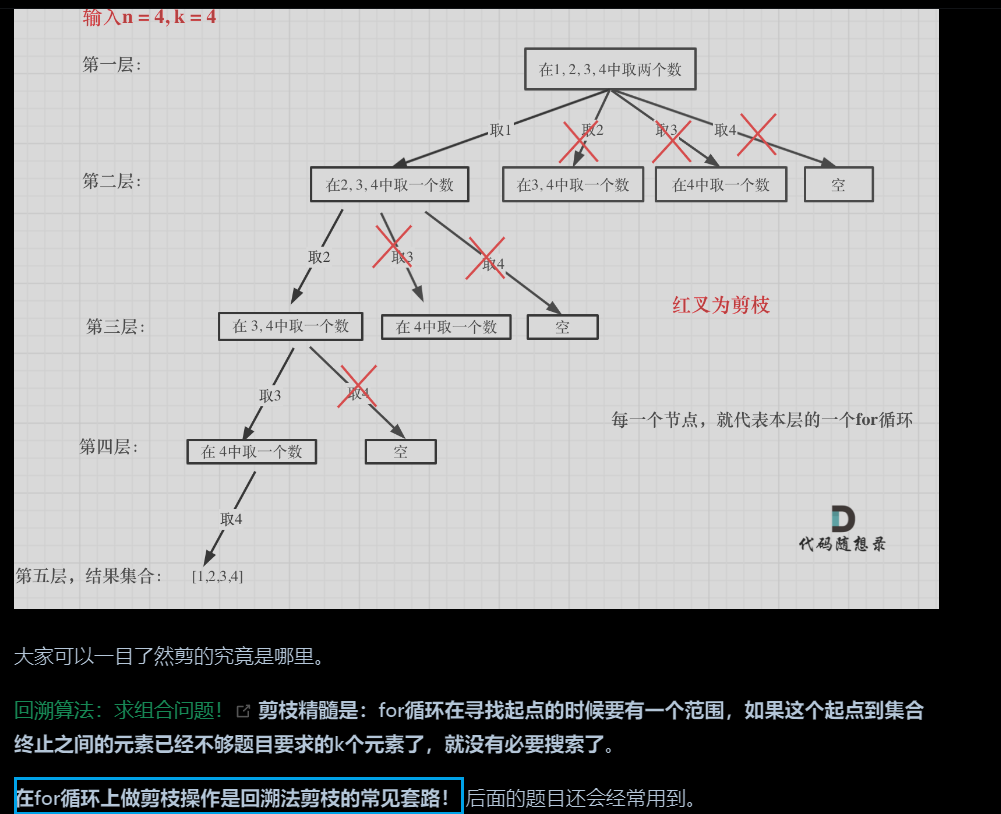
-
组合总和问题
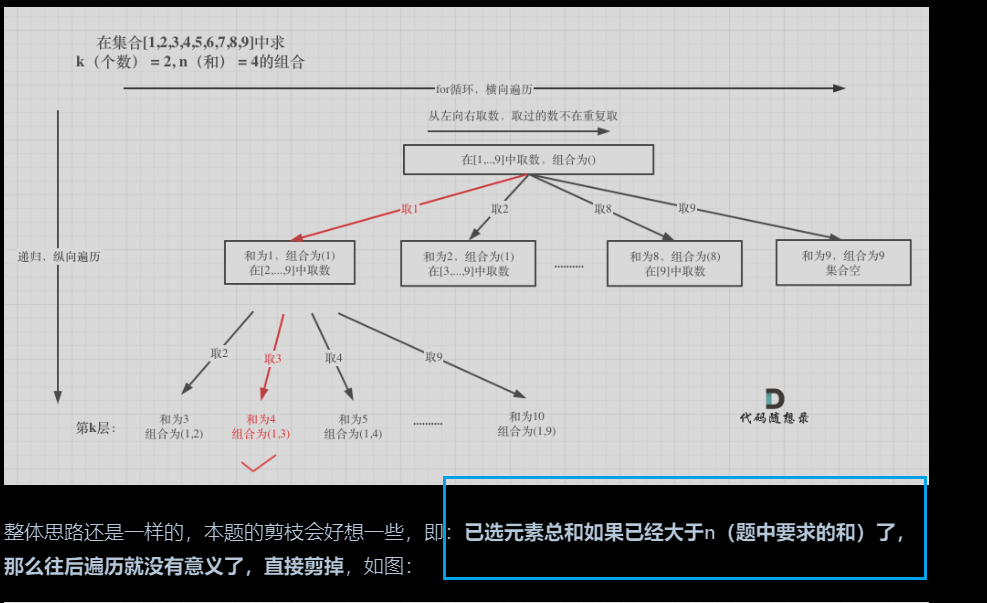
-
组合总和(三)—>集合中有重复元素
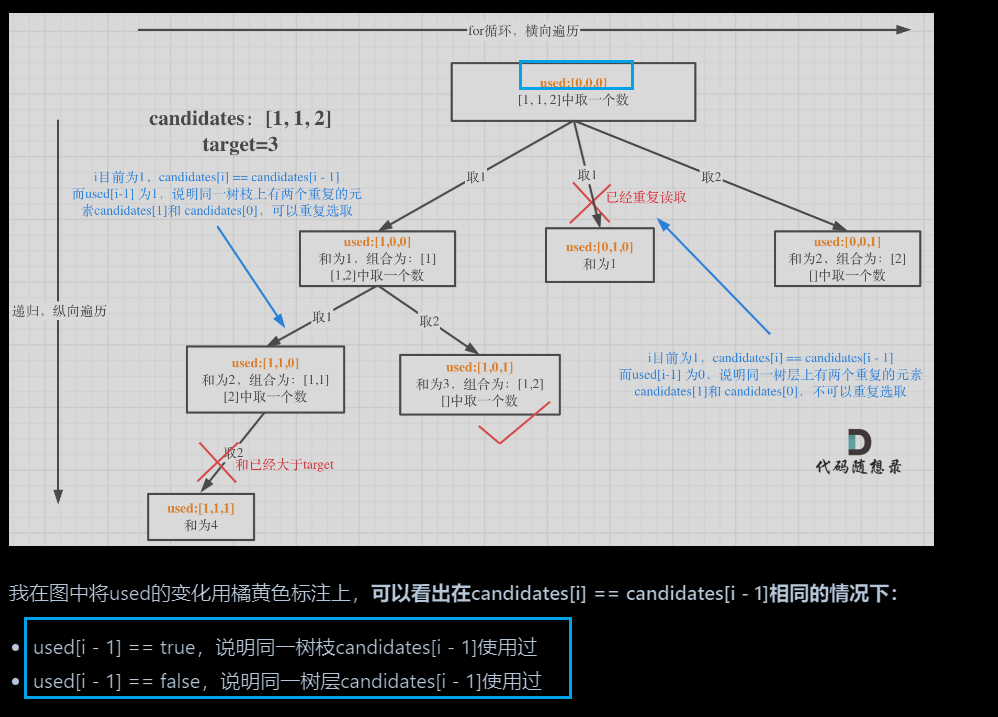
-
电话问题—>多个集合求组合
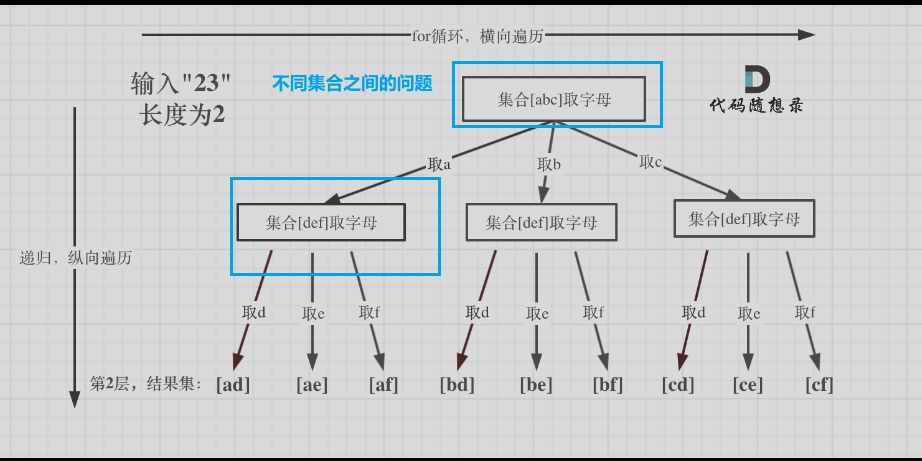
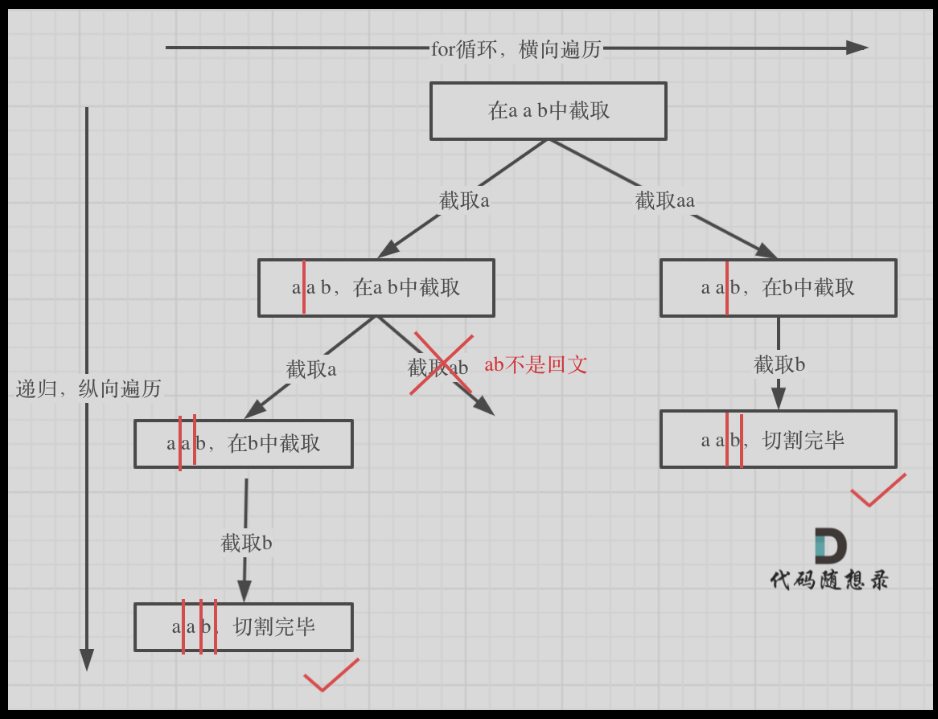
2.切割问题
-
用求解组合问题的思路来解决

3.子集问题
-
在树形结构中子集问题是要收集所有节点的结果,而组合问题是收集叶子节点的结果。
-
普通子集问题一定要排序,不能简单用哈希数组去重,因为
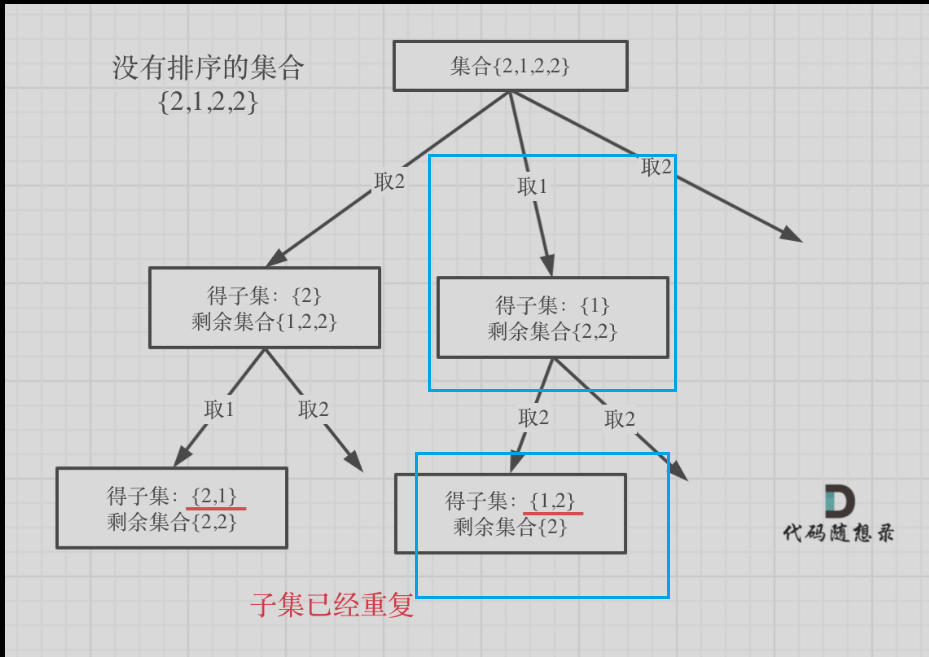
与递增子序列区分开来
-
子集问题(一)
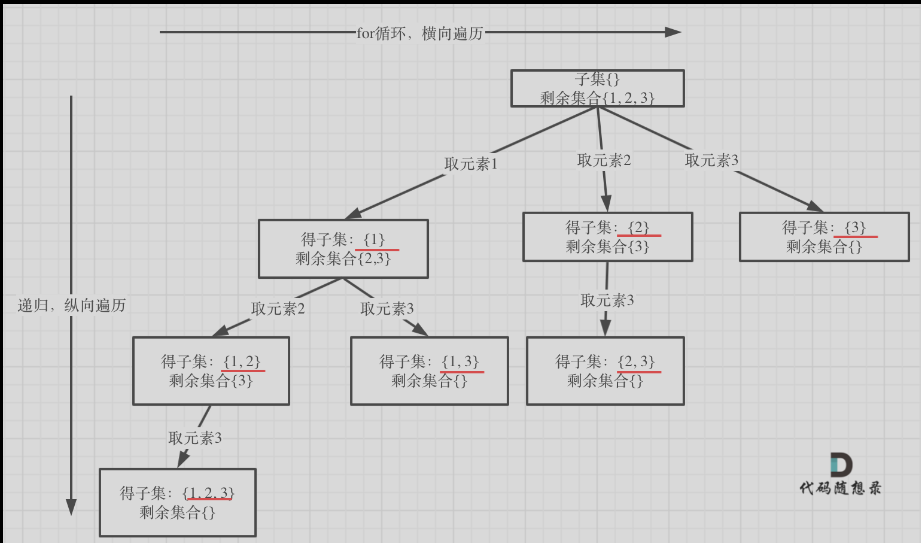
-
子集问题(二)
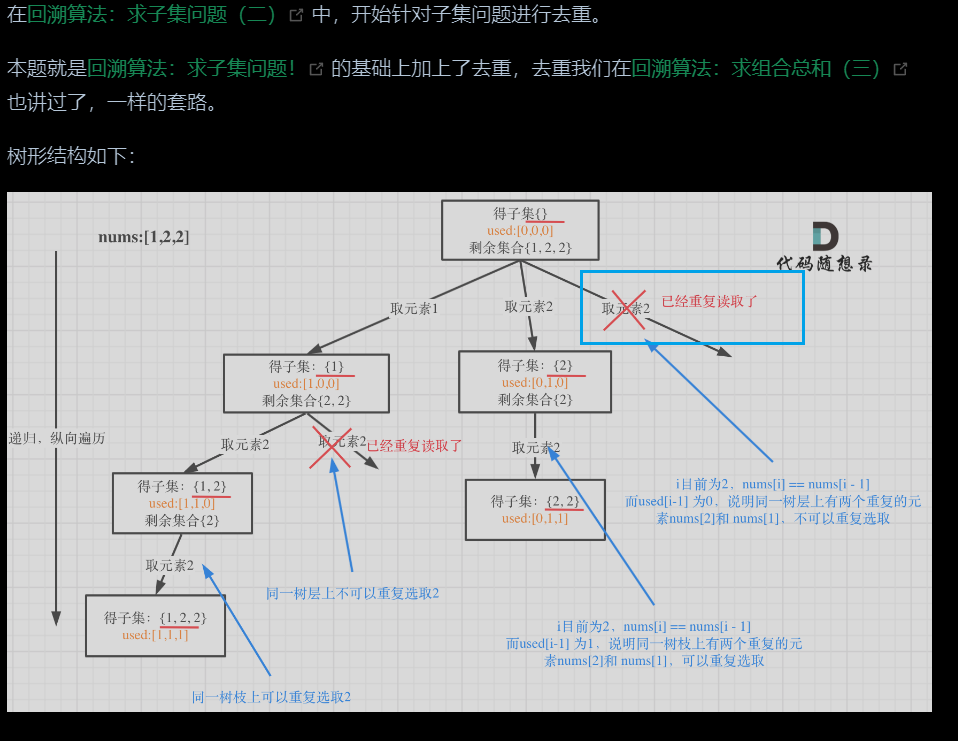
-
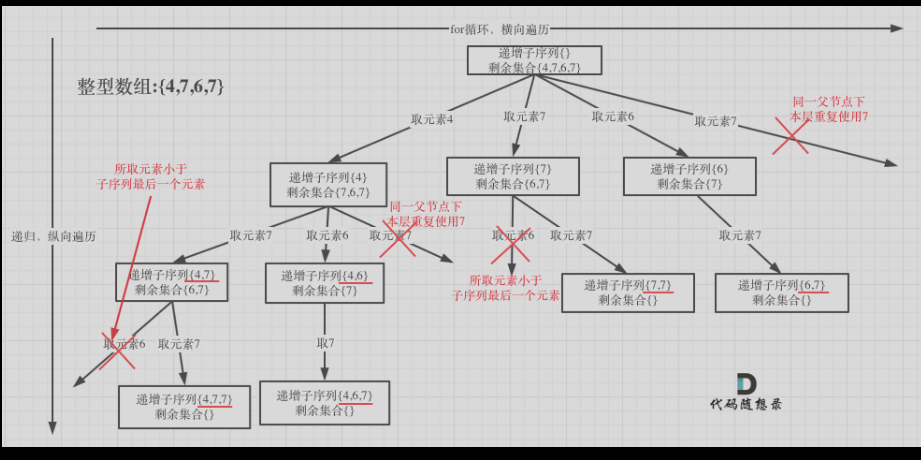
递增子序列
- 特点为:不能是排好序的数组,要借助哈希数组,层间去重,与子集问题区分开来
4.排列问题
- 特点:
- 每层都是从0开始搜索而不是startIndex
- 需要used数组记录path里都放了哪些元素了(树枝去重)
-
普通排列:
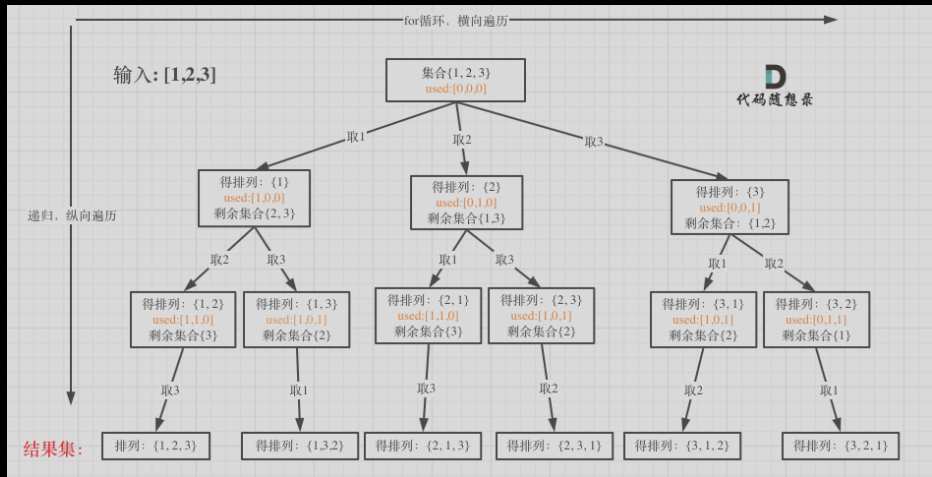
-
排列问题(树层去重)
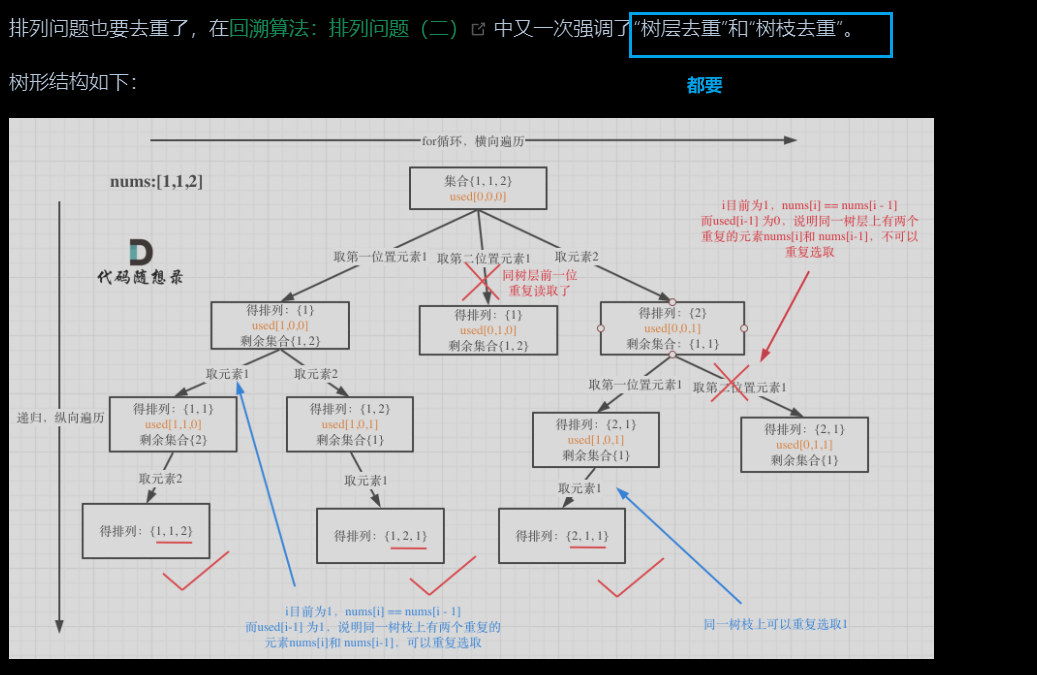
5.棋盘问题(未完待续)
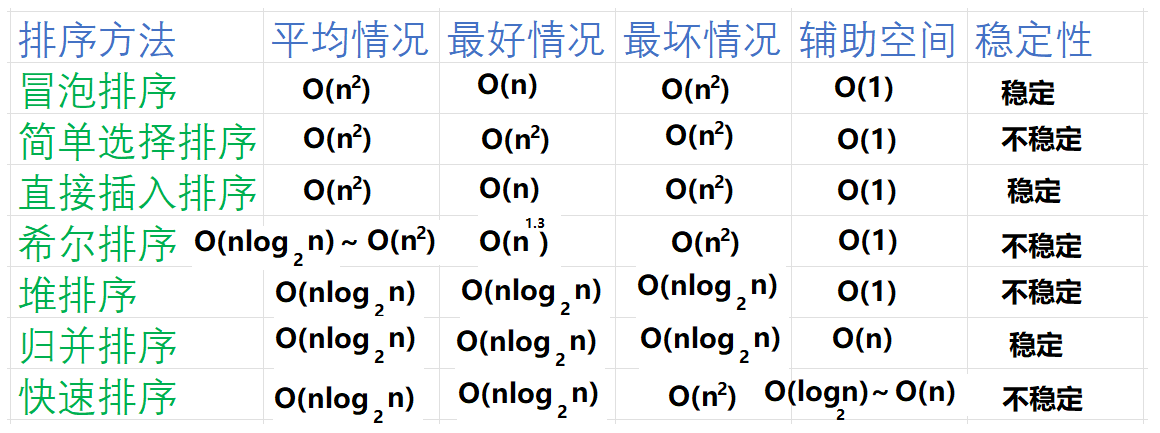
6.复杂度分析