A Dual Augmented Two-tower Model for Online Large-scale Recommendation

美团的对偶增强双塔为了user塔和item塔操碎了心，众所周知，双塔的一个大毛病就是item和user的交叉太晚，重要的信息经过层层神经网络的抽象提取，有些重要的信息活不到交叉的那一刻就在中途丢失了。怎么尽早实现user塔和item塔的交叉是个让大家都想破脑袋的事，腾讯的MVKE通过全局向量作为桥梁，一桥架起双塔，实现早期的user塔和item的交叉，在实际业务中落地效果不错，美团的DAT通过在user塔和item塔分别构造一个增强向量，user塔的增强向量作为user塔输入的一部分，去学item塔的输出，item塔的增强向量作为item塔输入的一部分，去学user塔的输出，从而实现user塔和item塔的交叉。这个做法也是非常巧妙。

做法

结构如图

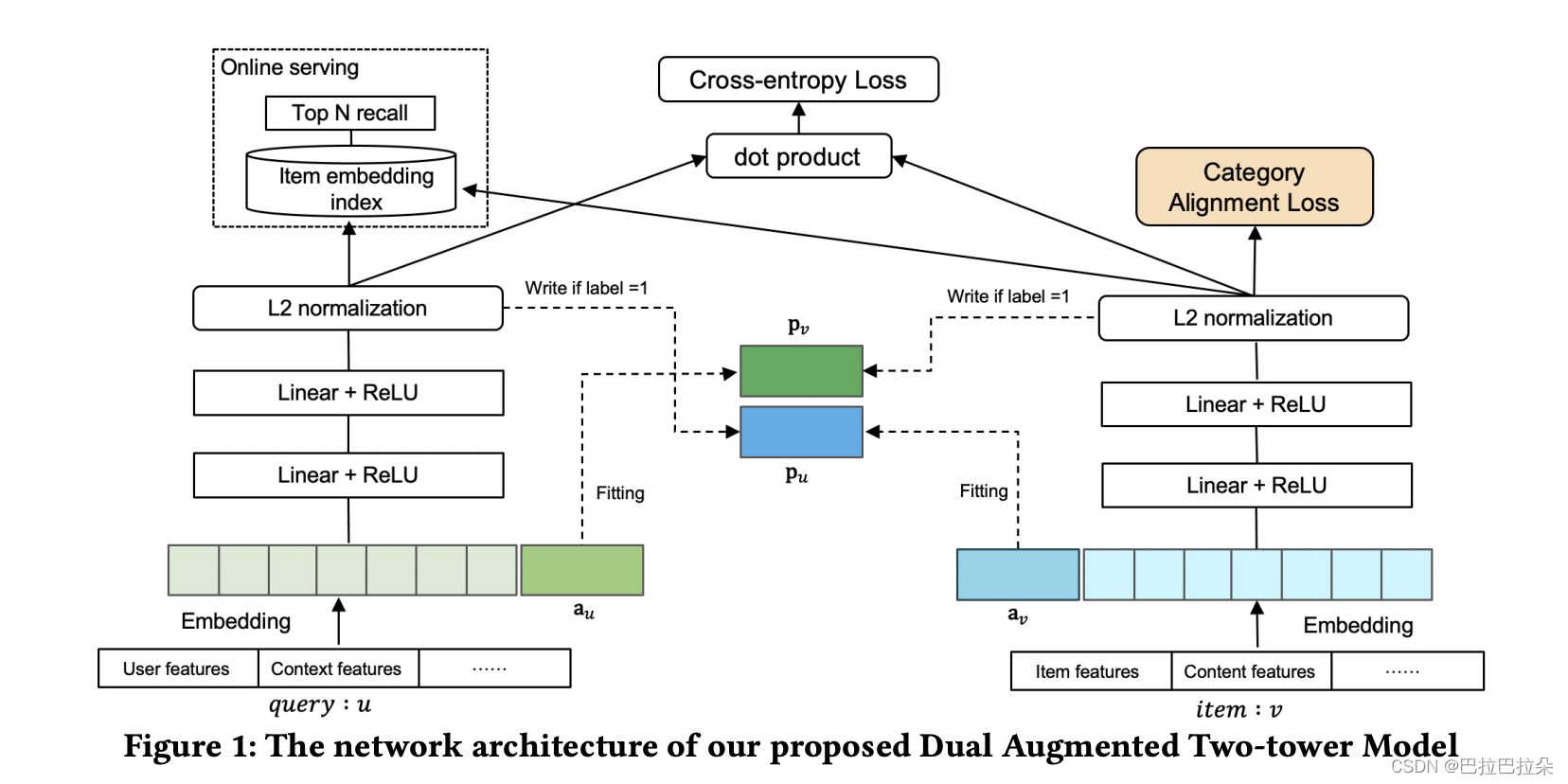
可以看到，一个重要的改动就是user塔的Embedding层多了一个增强向量${\mathbf{a}}_u$，item塔的Embedding多了一个增量向量${\mathbf{a}}_v$，user塔的增强向量${\mathbf{a}}_u$学习item塔的最终输出向量${\mathbf{p}}_v$，item塔的增强向量学习user塔最终输出向量${\mathbf{p}}_u$。

同时user塔的增强向量${\mathbf{a}}_u$也作为user塔的Embedding输入，作为user塔炼丹原材料，最终产出用户塔的输出${\mathbf{p}}_u$，也就是item塔的信息实际上成为了user塔输入的一部分，item塔也是同样的操作。这样就实现了item塔和user的尽可能早的交叉。

详细做法

输入侧，以用户塔为例，第$i$个特征域的Embedding记为${\mathbf{e}}_i$，用户侧的各个特征域(年龄、性别、地域、…)拼接起来就是如下
$$[{\mathbf{e}}_1,{\mathbf{e}}_2,...{\mathbf{e}}_n]$$
再拼接上构造的用户侧增强向量${\mathbf{a}}_u$，用户侧Embedding可以表示为
$$\mathbf{z}=[{\mathbf{e}}_1,{\mathbf{e}}_2,...{\mathbf{e}}_n,{\mathbf{a}}_u]$$
经过炼丹炉炼制，炼制过程表示为
$${\mathbf{h}}_1=ReLU({\mathbf{W}}_1\mathbf{z}+{\mathbf{b}}_1)$$
$${\mathbf{h}}_L=ReLU({\mathbf{W}}_l{\mathbf{h}}_{L-1}+{\mathbf{b}}_l)$$
$${\mathbf{p}}_u=L2Norm({\mathbf{h}}_L)$$
同理可以炼制item塔，得到item塔输出${\mathbf{p}}_v$

那么增强的向量怎么学习塔对面的输出呢，每个增强向量通过一个辅助loss的方式，这个辅助loss在论文中称为AMM(Adaptive-Mimic Mechanism)，对label为1（y=1）的样本计算辅助loss，其实就是要求这2个向量是一致的，形式如下
$$los{s}_u=\frac{1}{T}\sum y({\mathbf{a}}_u-{\mathbf{p}}_v{)}^2$$
$$los{s}_v=\frac{1}{T}\sum y({\mathbf{a}}_v-{\mathbf{p}}_u{)}^2$$

*因为这个loss是为了更新增强向量用的，所以需要固定${\mathbf{p}}_v$和${\mathbf{p}}_u$，反向传播的时候，需要阻塞loss对${\mathbf{p}}_v$和${\mathbf{p}}_u$的梯度更新。

类目信息迁移

业务生产中，各个item所属的类目通常是极度不均衡的，有的类目包含的item少，有的类目包含的item多，通常包含较少类目的item学习可能会不充分，这里设置了一个loss来让占主导的类目信息往长尾类目信息上面迁移。通过占主导的类目协方差和其他类目协方差的模来约束。
$$los{s}_{CA}=\sum _{i=2}^m||C(S^{major})-C(S^i)|{|}_F^2$$

loss计算

主loss，item塔的输出和user塔的输出$s(u,v)=<{\mathbf{p}}_u,{\mathbf{p}}_v>$

$$los{s}_p=-\frac{1}{T}\sum (y\log \sigma (<{\mathbf{p}}_u,{\mathbf{p}}_v>)+(1-y)\log (1-\sigma (<{\mathbf{p}}_u,{\mathbf{p}}_v>)))$$

最后的loss为

$$loss=los{s}_p+{\lambda }_{1}los{s}_u+{\lambda }_{2}los{s}_v+{\lambda }_{3}los{s}_{CA}$$

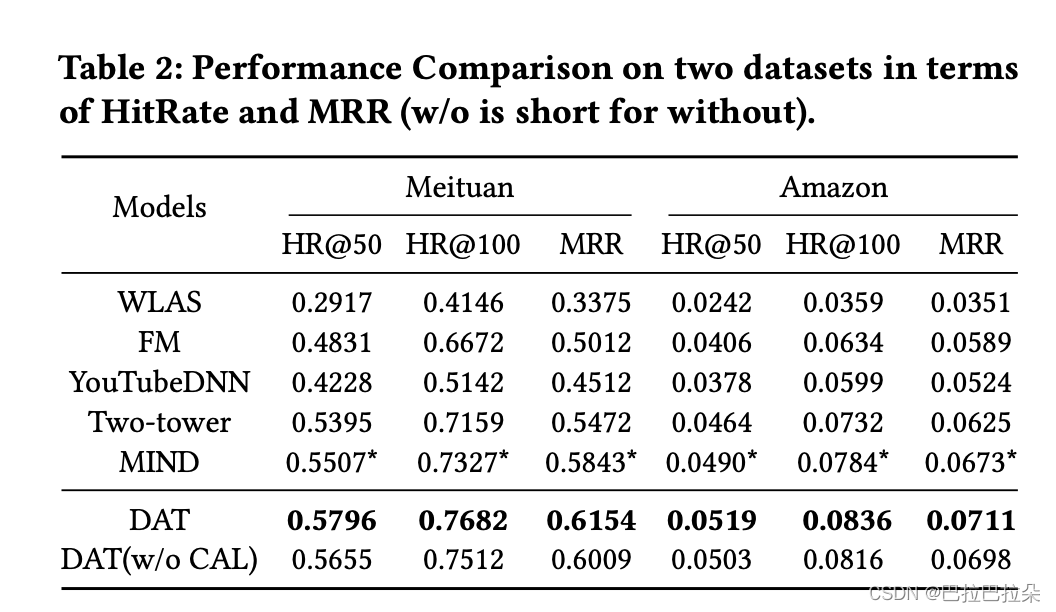
实验效果

可以看到加了增强向量的双塔效果还是不错的。

论文地址：https://dlp-kdd.github.io/assets/pdf/DLP-KDD_2021_paper_4.pdf