文章目录
- 七大排序的分类
- 时间复杂度
- 空间复杂度
- 稳定性
- 直接插入排序
- 希尔排序
- 选择排序
- 堆排序
- 冒泡排序
- 快速排序
- 归并排序
- 总结
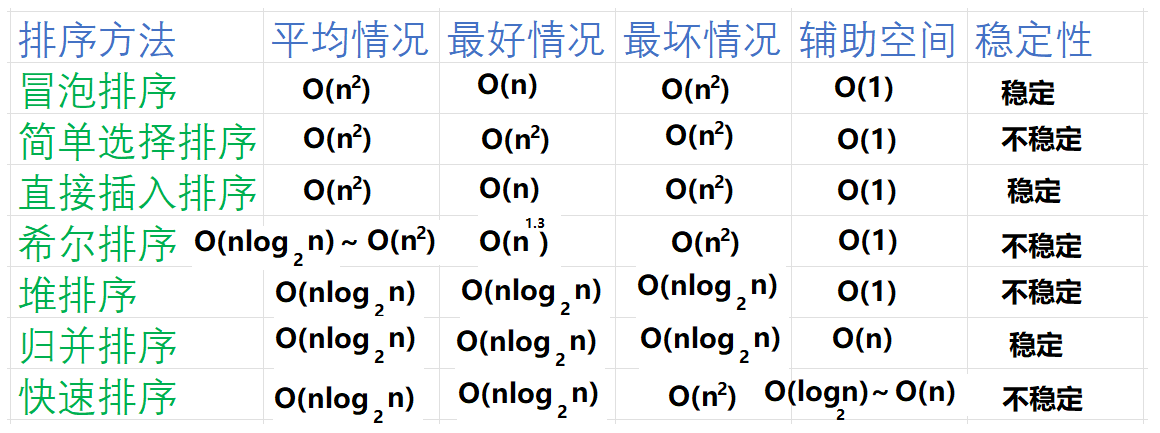
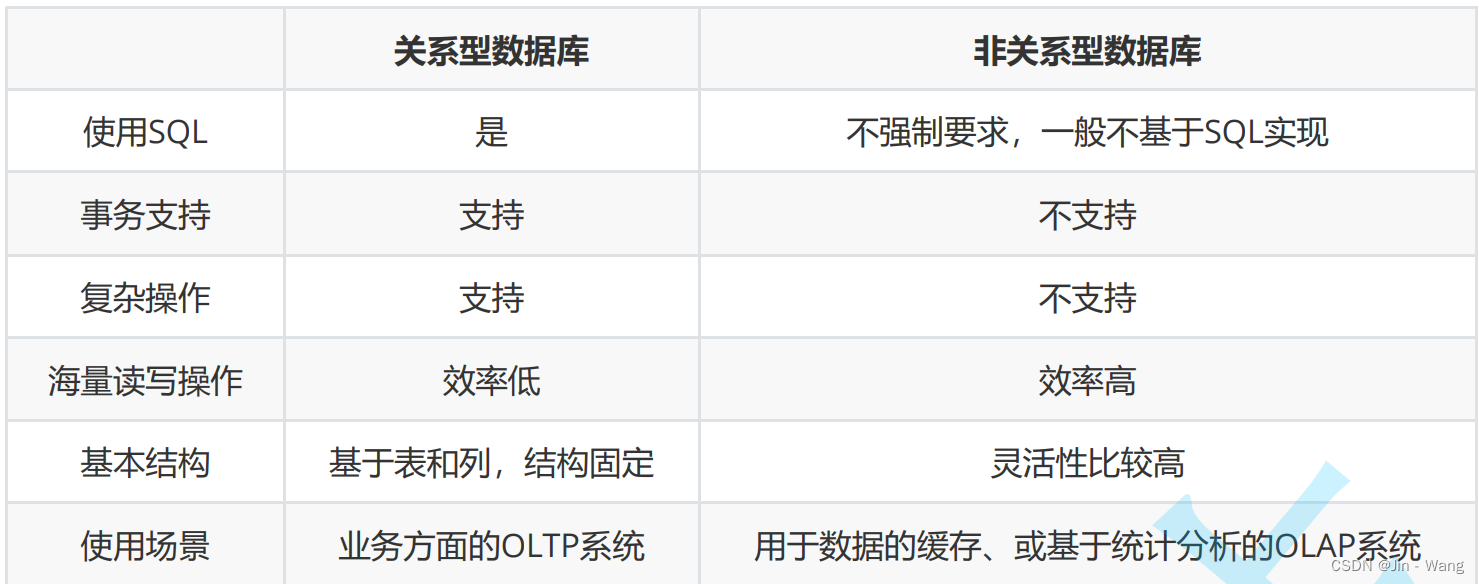
七大排序的分类
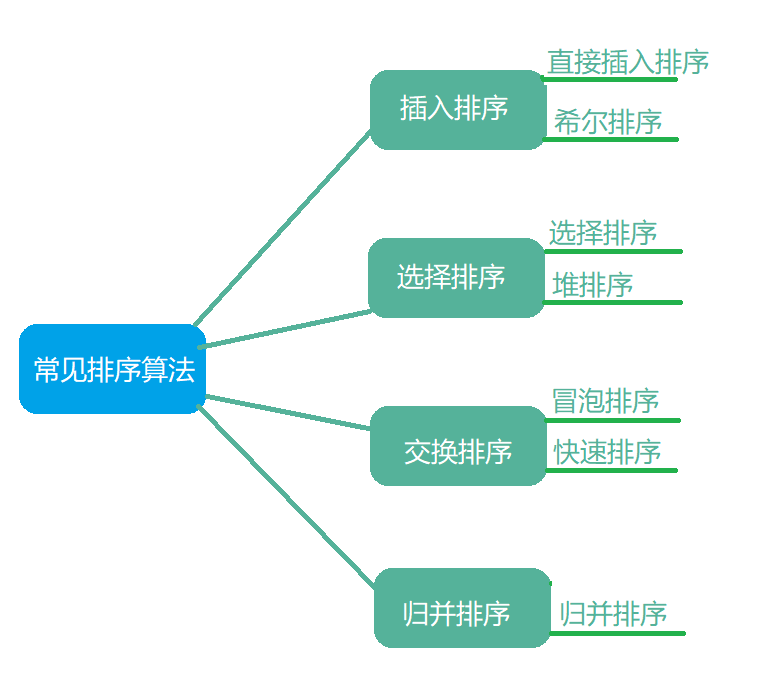
时间复杂度
时间复杂度是指一个程序中基本语句被执行的次数,一般认为是最坏情况。
空间复杂度
空间复杂度是指在一个程序执行时要额外开辟的空间大小。
稳定性
什么是稳定性呢?这里的稳定性不是指时间复杂度稳定,而是原数据中相同值的前后位置是否会发生改变。
例如 1 2 1 4 5如果在排序的过程中第二个1跑到了第一个1的前面,那么我们就说这个排序不稳定,记住是相同值的前后位置。当然是指有能力做到稳定我们就说它稳定,如果想让一个排序不稳定我们都能做到让它不稳定。
直接插入排序
直接插入排序就是从第i个数开始依次向前i-1个有序数中插入。
//插入排序
void InsertSort(int* a, int n)
{
assert(a);
//将无序数组排成有序
//从第一个值开始向前比较,前n个值有序再让第n+1个值插入,前面的有序数组
for (int end = 1; end < n; end++)
{
//单趟排序 将一个值插入一个有序数组
//值会被覆盖,所以要提前保存
int x = a[end];
int j;
for (j = end - 1; j >= 0; j--)
{
//此时n是最后一个元素的下标
if (x < a[j])
{
a[j + 1] = a[j];
}
else
{
break;
}
}
a[j + 1] = x;
}
}
最好情况时,数组是有序的,时间复杂度为O(n)
最坏情况时,数组是逆序的,时间复杂读为1/2 * n * (n + 1),所以对应的也就是O(n2)
所以直接插入的时间复杂度为O(n)~O(n2)
空间复杂度:O(1)
稳定性:稳定
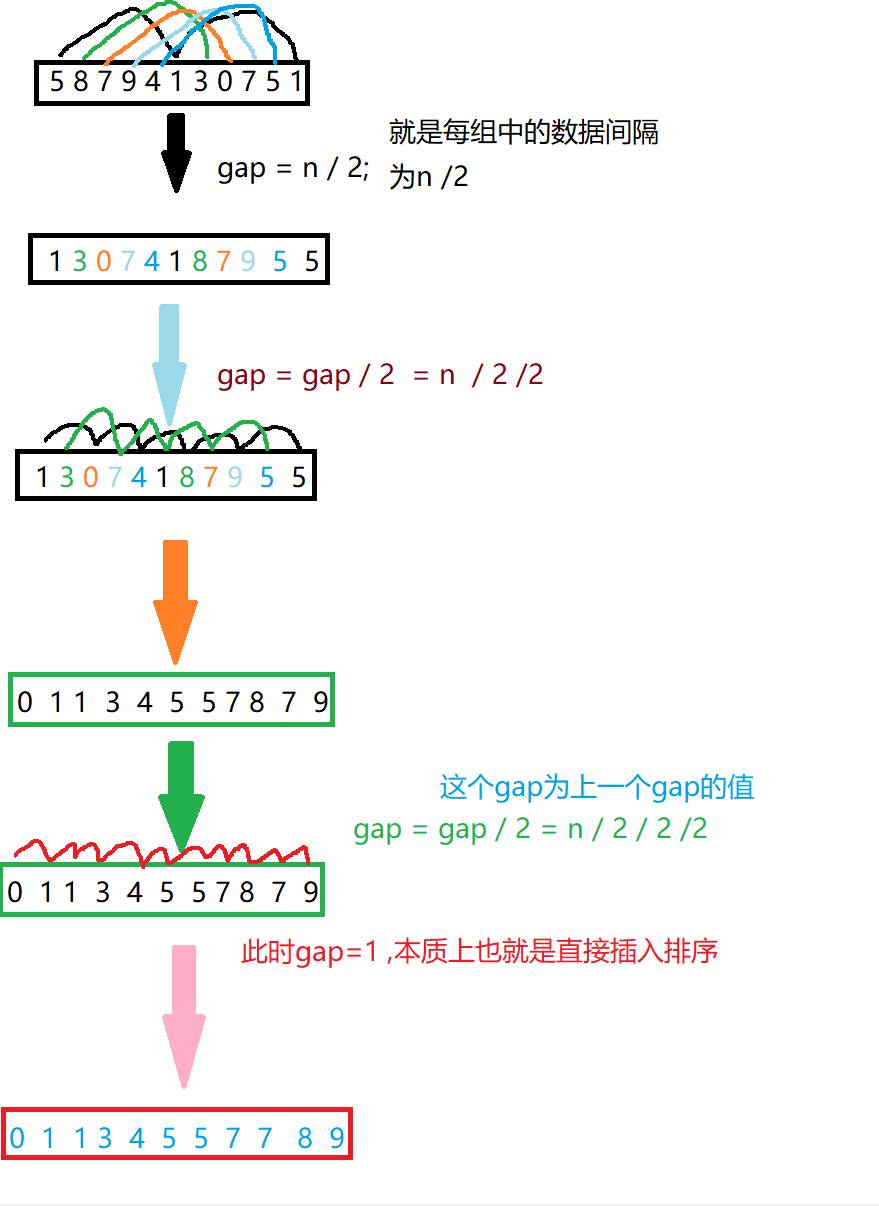
希尔排序
希尔排序就是把数据进行分组,然后对每组数据进行排序,每组的数据个数逐渐增加,被分成的组数也就逐渐变少。
// gap > 1 预排序
// gap == 1 直接插入排序
void ShellSort(int* a, int n)
{
//思想:分组排序,让数据尽量有序,接着让间距gap逐渐减小到1
//gap例如 gap = 2时,1,3,2,4,5----1,2,5是一组,3,,4是一组
int gap = n;
int end = 0;
while (gap > 1)
{
gap /= 2;
//选定要插入的数据
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
//插入
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
当然这里的gap也可以是n/3
至于时间复杂度:
希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就
会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。 - 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的
希尔排序的时间复杂度都不固定:
《数据结构(C语言版)》— 严蔚敏

空间复杂度这里我们就很容易计算,因为都是在原数组上进行操作的,所以空间复杂度为O(1)
稳定性:不稳定
选择排序
选择排序:从第当前位置开始依次向后遍历找到最大或最小(降序或升序)然后和它交换。
我们也可以同时记录两个位置找到最大和最小。在升序中让最小和第i位置交换,让最大和第n-1-i位置交换,此外还要考虑到一种特殊情况第i位置就是最大值时,在找到最小后它和下标为min的最小值交换了,所以此时第n-1-i位置就要和min位置的值交换了。

//方法二
void SelectSort(int* a, int n)
{
int left, right;
int mini, maxi;
left = 0;
right = n - 1;
while (left < right)
{
mini = left;
maxi = left;
for (int i = left + 1; i <= right; i++)
{
//找出最大和最小值的下标
if (a[i] < a[mini])
{
mini = i;
}
if (a[i] > a[maxi])
{
maxi = i;
}
}
Swap(&a[left], &a[mini]);
//要考虑最初定义的mini是不是max,如果是那么在上面的交换后,它就被换走了。
if (maxi == left)
{
Swap(&a[right], &a[mini]);
}
else
{
Swap(&a[right], &a[maxi]);
}
left++;
right--;
}
}
这里是同时找最大和最小,单项选择和双向选择的区别就是,双向选择可以少走一些选择的过程,但是对应的时间复杂度并没有发生改变都是O(n2)。
单向:1/2*(n-1 + 1)* 对应的量级就是O(n2)
双向:大致 1/2*(n-1 + 2)n1/2 因为它少走了一般的路程所以要除以2,但是量级没有改变,仍是O(n2)
直接选择排序与原数据顺序无关。
空间复杂度:O(1)
稳定性:不稳定
堆排序
堆排序,要先进行建堆,大根堆或者小根堆,再根据topk问题原理将topk与最后一个值交换,所以此时最后一个值也就在第一个位置,再让它进行向下调整。
向上建堆的过程时间复杂度为:最差为n*logn-n
调整的时间复杂度:
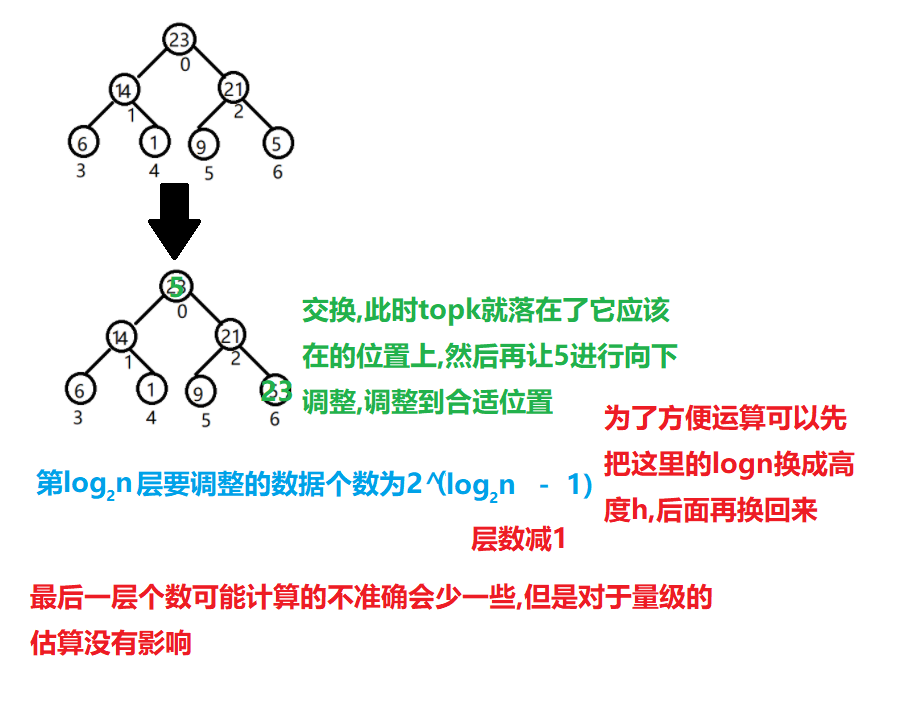
一共有log2n层,从第1层开始向下调整,调整次数由n到1,调整的数据个数也由2^(n-1) 到 2^1个
然后利用错位相减法得到的结果是log2n * h * 2^(h - 1),其中h * 2^(h - 1)也就数据的总个数n,所以就可大致得出时间复杂度为O(n*log2n),堆排序不会受原数据顺序的影响,因为都要从top开始向下调整到最后。
空间复杂度:都是在原数组上进行操作的,只有一些额外的临时变量,可归为O(1)
稳定性:不稳定 例如对大根堆排升序时,数组值顺序为2 2 1,第一次调完之后就变成了 2 1 2
注意这里粗体和斜体2的位置变化
冒泡排序
void BubbleSort(int* a, int n)
{
assert(a);
assert(n);
for (int i = 0; i < n; i++)
{
bool exchange = false;
for (int j = 1; j < n - i; j++)
{
if (a[j] < a[j - 1])
{
Swap(&a[j], &a[j - 1]);
exchange = true;
}
}
if (exchange == false)
{
break;
}
}
}
冒泡排序的时间复杂度:
冒泡排序的基本语句就是Swap语句
Swap执行次数由n次逐渐减少到1次。
所以执行总次数为[ n*(1+n)] / 2。所以时间复杂度为N^2;(计算复杂度时系数可以省略,粗略计算n+1近似于n)
当原数据本来就有序时,只需遍历一遍即可,判断一下数据有么有发生交换,因为有序所以没有交换,就可直接跳出,此时的时间复杂度为O(N)。
所以综上所述冒泡排序与原数据有关,时间复杂度为O(N)~O(N^2)。
冒泡排序的空间复杂度:
这里的数组空间是已经开辟好的,不属于在这个排序空新开辟的,所以不计算在内。而这里只有一些i,j等变量属于新开辟的,且它们只开辟一次空间就够了,后面会重复利用,即所有的i,j都共用一个存储空间, 所以他们是属与O(1)这个量级的,即它的空间复杂度为0(1);
稳定性:稳定
快速排序
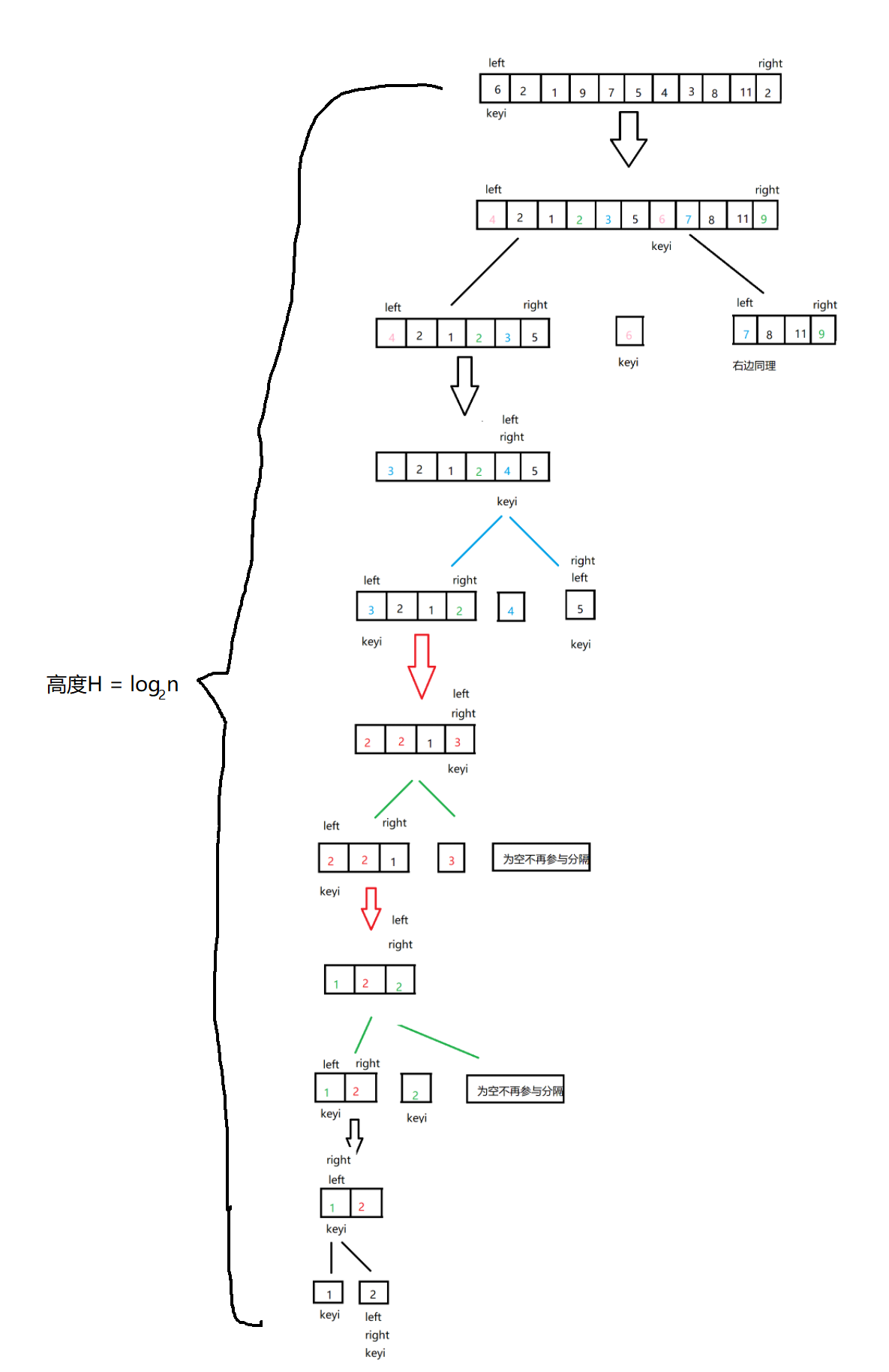
// 快速排序hoare版本
int PartSort1(int* a, int left, int right)
{
//设一个数作为基准,我们一般选择最左边或者是最右边的数作为基准,
//最终结果是基准的左右两边分别大于和小于它或小于大于它,具体看是排升序还是降序
//我们以排升序举例
//int keyi = left;
//如果数据已经接近有序,那么直接选取某一个数作为基准很有可能会导致栈溢出,
int midi = GetMidIndix(a, left, right);
//让选择的基准和最左边的值换位置
Swap(&a[midi], &a[left]);
int keyi = left;
while (left < right)
{
//找小
//考虑特殊情况 数据全相等,
//数据本来就是非降序排好的
while (left < right && a[right] >= a[keyi])//为什么要加等于号?
{
right--;
}
while (left < right && a[left] <= a[keyi])
{
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[keyi], &a[left]);
return left;//返回a[keyi]现在所在的下标,就是为了找到将数据一分为二的下标,一边比它大一边比他小
}
快速排序也与原数据有关,是否接近有序,它的最好情况时时间复杂度为nlogn
如上图递归深度为logn,每一层比较的数都为n,最后几层可能会不为n,但是也接近,所以比较执行的总次数为nlogn。
当它为逆序时最坏,时间复杂度为n2,因为逆序所以它递归的深度为n,每一层比较的数都为n,最后几层可能会不为n,但是也接近,所以比较执行的总次数为N^2。
综上所述,快速排序最好情况时,时间复杂度为n*logn,最坏情况时复杂度为n^2。
空间复杂度:最好时递归深度为logn,最坏时递归深度为n,每次开辟的空间是为基准keyi开辟的,里面存放的就是基准下标,最好情况时要选logn次基准,最坏情况时要选n次基准,所以快速排序的空间复杂度为O(logn)~O(n)。
归并排序
我们这里说的归并排序是二路归并。
把每个元素都分开,然后两两合直到合并到没有元素,再合并的过程中进行排序。
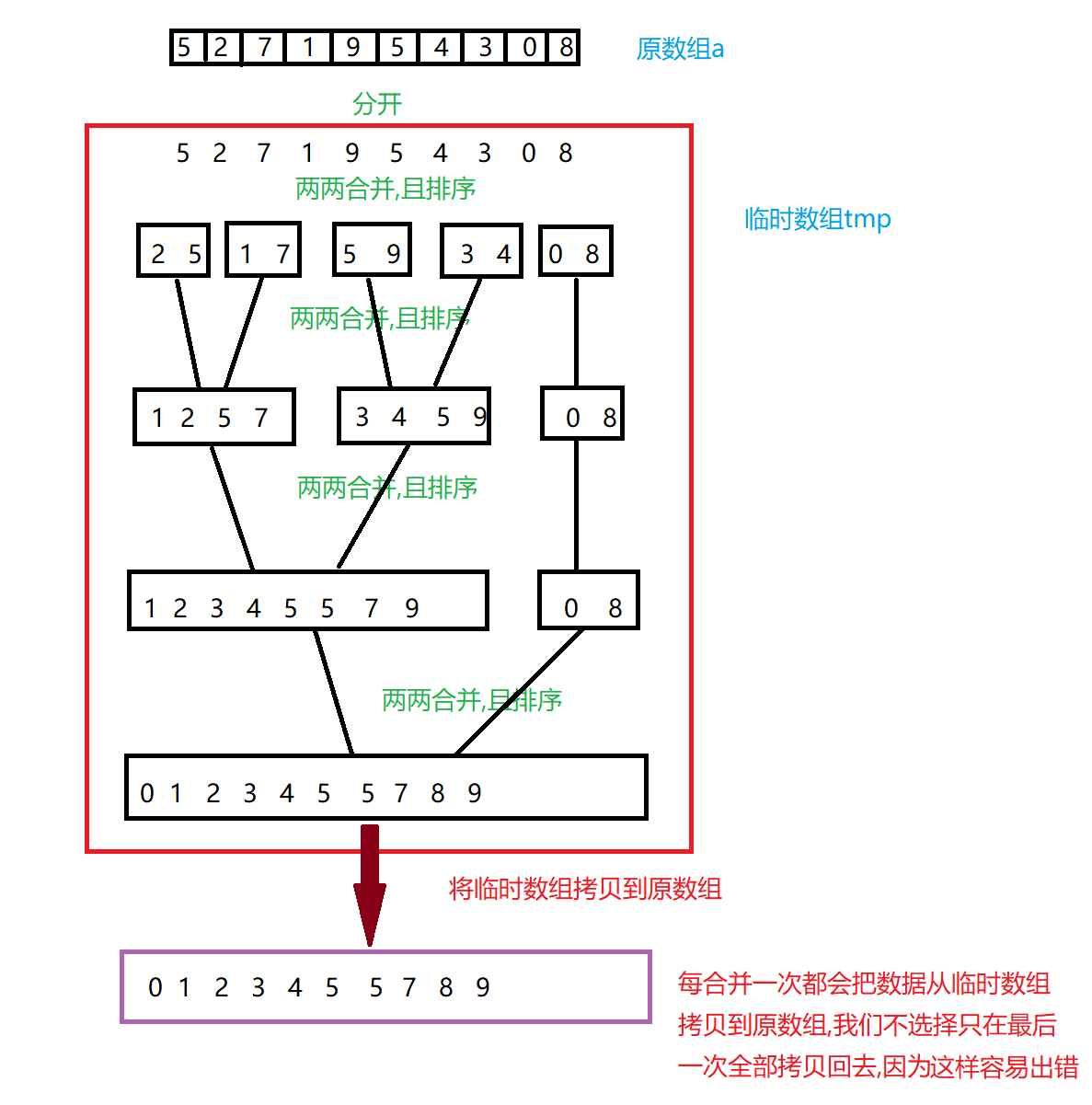
//递归实现
void _MergeSort(int* a, int begin, int end, int* tmp)
{
assert(a);
if (begin >= end)//有大于的情况吗?
{
return;
}
//归并排序实质上对应于后序遍历
// 求中位数是两边之和除以二
//int mid = (end - begin - 1) / 2;
int mid = (begin + end) / 2;
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid + 1, end, tmp);
int begin1 = begin;
int end1 = mid;
int begin2 = mid + 1;
int end2 = end;
//注意每次递归中的i等于begin
int i = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
//最后别忘了把数据拷贝到原数组
//注意拷贝的源位置和目标位置,要加上begin
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
归并排序应用的是标准的二分法,最好和最坏情况时间复杂度都是nlog2n,解释:一共需要分log2n层,每一层都有n个数据要进行比较,且与原数据顺序无关。
空间复杂度:O(n)因为创建了一个临时数组tmp,且每次递归调用都是用的同一个临时数组,并不是开辟了nlog2n个临时空间。
稳定性:稳定
总结