wy的leetcode刷题记录_Day51

声明

本文章的所有题目信息都来源于leetcode
如有侵权请联系我删掉!
时间：2022-11-24

前言

795. 区间子数组个数

今天的每日一题是：795. 区间子数组个数

题目介绍

给你一个整数数组 nums 和两个整数：left 及 right 。找出 nums 中连续、非空且其中最大元素在范围 [left, right] 内的子数组，并返回满足条件的子数组的个数。

生成的测试用例保证结果符合 32-bit 整数范围。

示例 1：
输入：nums = [2,1,4,3], left = 2, right = 3
输出：3
解释：满足条件的三个子数组：[2], [2, 1], [3]

示例 2：
输入：nums = [2,9,2,5,6], left = 2, right = 8
输出：7

思路

方法一：双指针法：首先我们将数组中的数分为三部分：1.小于left；2.大于等于left并且小于等于right;3.大于right这三种，为了满足题意我们的子数组必须满足不存在3的情况下至少有一个情况2。我们遍历整个数组以此时的位置为右边界，每当出现情况2时我们更新一个变量last_1，该变量表示上一个情况2出现的位置，每当出现情况3时我们更新一个变量last_2并且将last_1置为-1（因为在last_2左边的数都不满足条件了），该变量表示上一个情况3出现的位置。当没有情况2 出现的时候说明此时以i为右边界的情况中不存在满足条件的情况，继续拓展右边界。当有情况2，无情况3的时候，说明左边界可以在[0,i]中任选。当有情况2，有情况3的时候，说明我们只能在[last_1,last_2]之间选择左边界才能满足条件。
方法二（来自题解）：计数法：根据方法一的结论，我们求出子数组必须满足不存在3的情况下至少有一个情况2的个数。所以，我们可以先求出只包含 0 或 1 的子区间数目，再减去只包括 0 的子区间数目。我们使用了一个辅助函数用来计算数组 nums 中所有元素小于等于 lower 的子数组数目。

代码

双指针法：

class Solution {
public:
    int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {
        int n=nums.size();
        int ans=0;
        for(int i=0;i<n;i++)
        {
            if(nums[i]<left)
                nums[i]=0;
            else if(nums[i]>=left&&nums[i]<=right)
                nums[i]=1;
            else if(nums[i]>right)
                nums[i]=2;
        }
        int last_1=-1;
        int last_2=-1;
        for(int i=0;i<n;i++)
        {
            if(nums[i]==1)
                last_1=i;
            else if(nums[i]==2)
            {
                last_1=-1;
                last_2=i;
            }

            if(last_1!=-1)
                ans+=last_1-last_2;
        }
        return ans;
    }
};

计数法：

class Solution {
public:
    int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {
        return count(nums, right) - count(nums, left - 1);
    }

    int count(vector<int>& nums, int lower) {
        int res = 0, cur = 0;
        for (auto x : nums) {
            cur = x <= lower ? cur + 1 : 0;
            res += cur;
        }
        return res;
    }
};

收获

简单的模拟题，需要考虑一些情况，但没有特别复杂的情况

98. 验证二叉搜索树

题目介绍

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

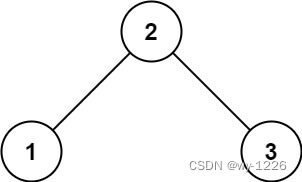
输入：root = [2,1,3]
输出：true

示例 2：

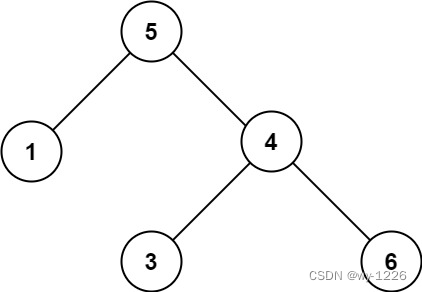
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

思路

根据搜索树的性质，我们通过中序遍历的方法得到一个数组，这个数组在基于搜索树的性质上一定是一个严格升序数组，所以我们基于此判定即可，同理可写出递归和递推。

代码

递归：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> arr;
    bool isValidBST(TreeNode* root) {
        travel(root);
        int n=arr.size();
        for(int i=1;i<n;i++)
        {
            if(arr[i]<=arr[i-1])
                return false;
        }
        return true;
    }
    void travel(TreeNode* root)
    {
        if(root==nullptr)
            return;
        travel(root->left);
        arr.push_back(root->val);
        travel(root->right);
    }
};

递推：

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        stack<TreeNode*> stack;
        long long inorder = (long long)INT_MIN - 1;

        while (!stack.empty() || root != nullptr) {
            while (root != nullptr) {
                stack.push(root);
                root = root -> left;
            }
            root = stack.top();
            stack.pop();
            // 如果中序遍历得到的节点的值小于等于前一个 inorder，说明不是二叉搜索树
            if (root -> val <= inorder) {
                return false;
            }
            inorder = root -> val;
            root = root -> right;
        }
        return true;
    }
};