省份数量

难度：中等
有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中省份的数量。

示例 1：

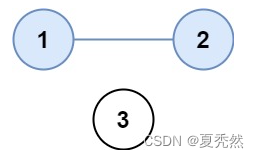
输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

示例 2：

输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

并查集

思路：
计算连通分量数的另一个方法是使用并查集。初始时，每个城市都属于不同的连通分量。遍历矩阵 $isConnected$，如果两个城市之间有相连关系，则它们属于同一个连通分量，对它们进行合并。
遍历矩阵 $isConnected$ 的全部元素之后，计算连通分量的总数，即为省份的总数。

时间复杂度： $O(n^{2}logn)$，其中 $n$ 是城市的数量。需要遍历矩阵 $isConnected$ 中的所有元素，时间复杂度是 $O(n^2)$，如果遇到相连关系，则需要进行 2 次查找和最多 1 次合并，一共需要进行 $2n^2$ 次查找和最多 $n^2$ 次合并，因此总时间复杂度是 $O(2n^2\log n^2)=O(n^2\log n)$。这里的并查集使用了路径压缩，但是没有使用按秩合并，最坏情况下的时间复杂度是 $O(n^2\log n)$，平均情况下的时间复杂度依然是 $O(n^2\alpha (n))$，其中 $\alpha$ 为阿克曼函数的反函数，$\alpha (n)$可以认为是一个很小的常数。
空间复杂度： $O(n)$，其中 $n$ 是城市的数量。需要使用数组 $roots$记录每个城市所属的连通分量的祖先。

class Solution:
    def findCircleNum(self, isConnected):
        def find(index):
            if roots[index] != index:
                roots[index] = find(roots[index])
            return roots[index]
        def merge(index1, index2):
            roota = find(index1)
            rootb = find(index2)
            if roota == rootb:
                return
            if deep[roota] > deep[rootb]:
                roots[rootb] = roota
            elif deep[roota] < deep[rootb]:
                roots[roota] = rootb
            else:
                roots[roota] = rootb
                rootb += 1
        cities = len(isConnected)
        deep = [1] * cities
        roots = list(range(cities))
        for i in range(cities):
            for j in range(i+1, cities):
                if isConnected[i][j] == 1:
                    merge(i, j)

        return sum(roots[i]==i for i in range(cities))

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/number-of-provinces