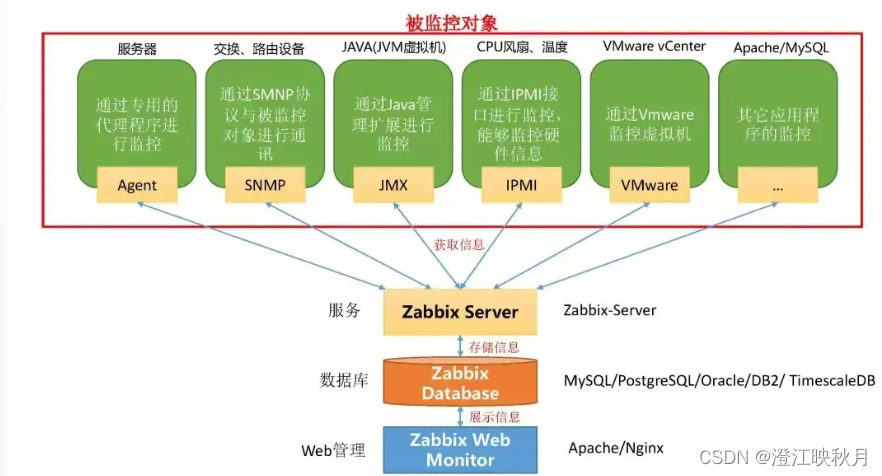
在上一节中《深度学习入门（6）误差反向传播基础---计算图与链式法则》，我们介绍了误差反向传播的计算图与导数计算的链式法则，这一节主要介绍计算图中各计算节点的误差反向传播计算方式，以及加法与乘法层的实现。

目录

1 误差的反向传播

1.1加法节点的反向传播

1.2乘法节点的反向传播

1.3 苹果的例子

2 简单层的实现

2.1乘法层的实现

2.2加法层的实现

2.3总结

---

1 误差的反向传播

1.1加法节点的反向传播

 

1.2乘法节点的反向传播

这里我们考虑z = xy。这个式子的导数用下式表示。

 

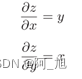
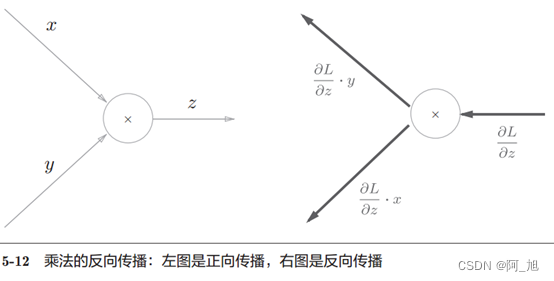
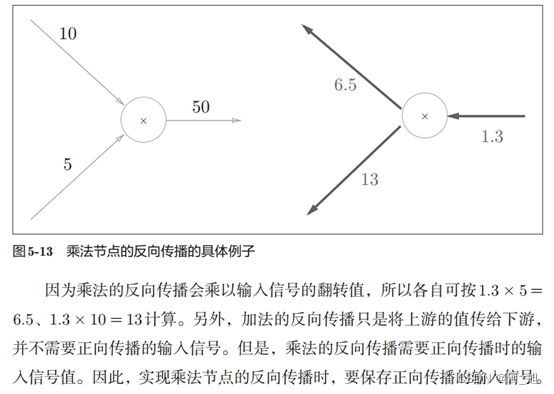
乘法的反向传播会将上游的值乘以正向传播时的输入信号的“翻转值”后传递给下游。翻转值表示一种翻转关系，如图5-12所示，正向传播时信号是x的话，反向传播时则是y；正向传播时信号是y的话，反向传播时则是x。

 

1.3 苹果的例子

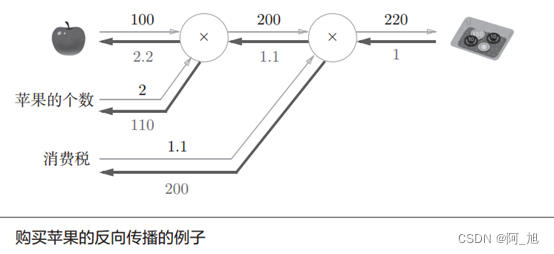
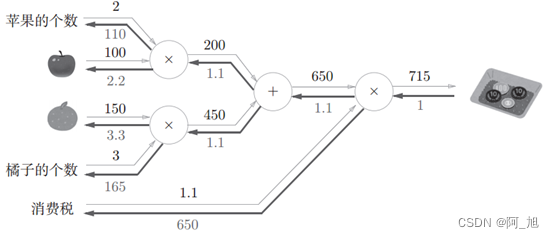
再来思考一下本章最开始举的购买苹果的例子（ 2个苹果和消费税）。这里要解的问题是苹果的价格、苹果的个数、消费税这3个变量各自如何影响最终支付的金额。这个问题相当于求“支付金额关于苹果的价格的导数”“支付金额关于苹果的个数的导数”“支付金额关于消费税的导数”。用计算图的反向传播来解的话，求解过程如图所示。

 

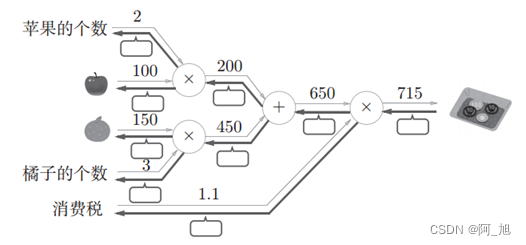
练习：

在图中的方块中填入数字，求各个变量的导数？

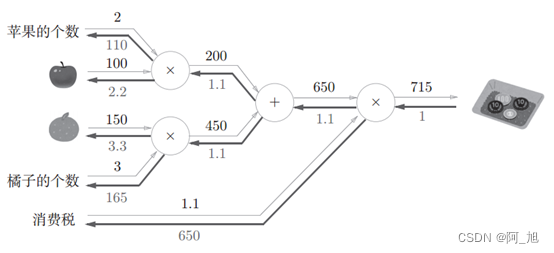
答案：

 

2 简单层的实现

我们把要实现的计算图的乘法节点称为“乘法层”（ MulLayer），加法节点称为“加法层” AddLayer）。

2.1乘法层的实现

层的实现中有两个共通的方法（接口）forward()和backward()。 forward()对应正向传播， backward()对应反向传播。

注：backward()将从上游传来的导数（ dout）乘以正向传播的翻转值，然后传给下游。

dout表示从上游传过来的导数。

举例：

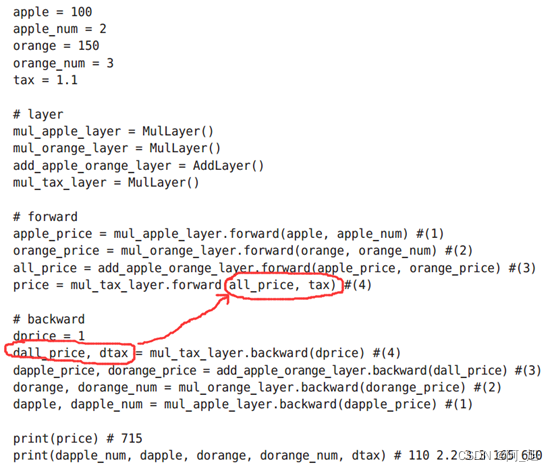
现在我们使用 MulLayer实现前面的购买苹果的例子（ 2个苹果和消费税）

 

 此外，关于各个变量的导数可由 backward()求出。

 这里，调用 backward()的顺序与调用 forward()的顺序相反。此外，要注意 backward()的参数中需要输入“关于正向传播时的输出变量的导数”。比如，mul_apple_layer乘法层在正向传播时会输出 apple_price，在反向传播时，则会将 apple_price的导数 dapple_price设为参数。

2.2加法层的实现

 

backward()将上游传来的导数（ dout）原封不动地传递给下游。

举例：

购买2个苹果和3个橘子的例子。

 

2.3总结

计算的大致步骤：

1，生成必要的层，

2，以合适的顺序调用正向传播的 forward()方法。

3，用与正向传播相反的顺序调用反向传播的 backward()方法，就可以求出想要的导数。

如果内容对你有帮助，感谢点赞+关注哦！

更多干货内容持续更新中…