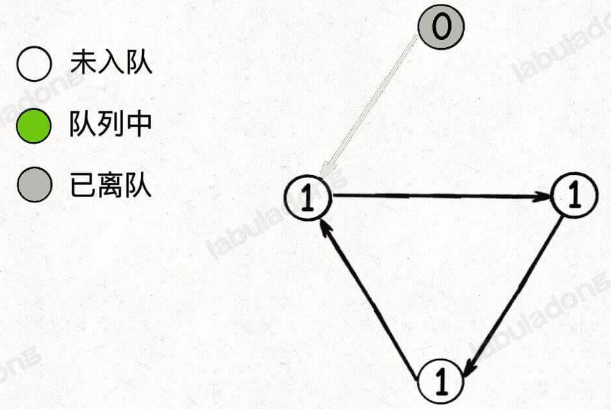
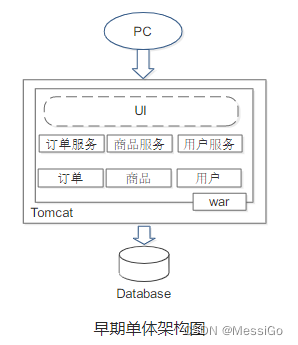
Amdahl定律

这个定律告诉我们去优化系统中最重要（占比最大）的部分，作业有个问题，是系统中有多个部件可以改进，可改进部分比例的分母是整个任务，并不是独属于部件$i$的任务，因此扩展的Amdahl定律为$S_n=\frac{1}{1-{\sum }_{i=1}^n{F}_i+{\sum }_{i=1}^n\frac{F_i}{S_i}}$。

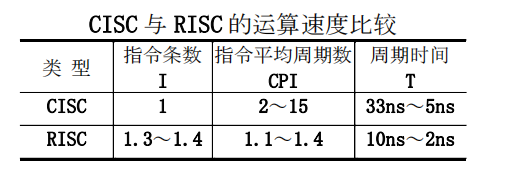
CPU性能公式

RISC思想的精华就是减少CPI，即每条指令的执行时间，同时会缩短时钟周期，而由于每条指令的功能简单了，完成相同的任务RISC需要更多的指令。

浮点数的表示公式

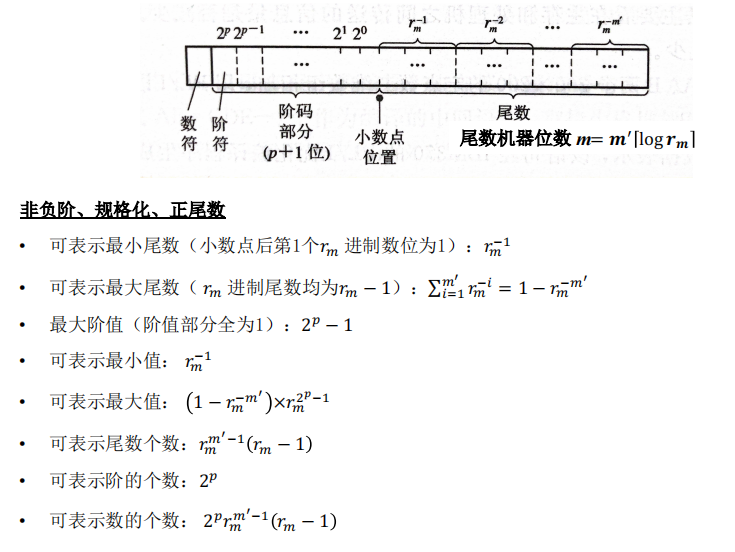
由于规格化的要求，尾数的第一位不能为0（基数为2的情况下一定是1），因此尾数第一位仅有$r_m-1$种可能，剩余$m^{\prime }-1$位均有$r_m$中可能，因此可表示尾数个数为$r_m^{m^{\prime }-1}(r_m-1)$。

• 随着$r_m$增大，可表示最小值减小，可表示最大值增大，可表示数的范围增大了
• 随着$r_m$增大，可表示数的个数也增大了

• 随着$r_m$增大，在与$r_m=2$表示的浮点数的重叠区域数的密度分布变稀疏了
• 随着$r_m$增大，数在数轴上的分布越稀疏，数的表示精度下降（不明白，感觉基呈一定倍数关系，比如$r_m=2,4$两种情形，基为4应该是可以表示2时候的所有数，因为使用的数字增多了，信息熵自然而然增多）
• 随着$r_m$增大，使得对阶移位的机会和次数减少，数的表示范围扩大，使尾数溢出需要右规的机会也变少，精度损失小
• 随着$r_m$增大，由于对阶或尾数溢出需右移及规格化需左移的次数减少，运算速度提高

Huffman编码法

huffman编码只可以很逼近上述的最短平均长度（理论上的最优值），因为受编码的长度必须为整数约束。Huffman编码可以用Amdahl定律的方式来理解，对最频繁出现的指令使用最短的编码（着重优化）。
但是huffman操作码的长度很不规整，硬件译码比较困难，与地址码共同组成固定长度的指令比较困难，因此一般使用扩展编码法，限定几种码长。仍然采用高概率指令使用短码、低概率指令使用长码的Huffman编码思想。