LeetCode算法小抄 -- 环检测算法 和 拓扑排序算法
- 环检测算法(DFS)
- [207. 课程表](https://leetcode.cn/problems/course-schedule/)
- 拓扑排序算法(DFS)
- [210. 课程表 II](https://leetcode.cn/problems/course-schedule-ii/)
- 环检测算法(BFS)
- 拓扑排序算法(BFS)
⚠申明: 未经许可,禁止以任何形式转载,若要引用,请标注链接地址。 全文共计6510字,阅读大概需要3分钟
🌈更多学习内容, 欢迎👏关注👀【文末】我的个人微信公众号:不懂开发的程序猿
个人网站:https://jerry-jy.co/
环检测算法(DFS)
207. 课程表
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
- 例如,先修课程对
[0, 1]表示:想要学习课程0,你需要先完成课程1。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
首先想到的就是把问题转化成「有向图」这种数据结构,只要图中存在环,那就说明存在循环依赖
class Solution {
// 记录一次递归堆栈中的节点
boolean[] onPath;
// 记录遍历过的节点,防止走回头路
boolean[] visited;
// 记录图中是否有环
boolean hasCycle = false;
public boolean canFinish(int numCourses, int[][] prerequisites) {
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
visited = new boolean[numCourses];
onPath = new boolean[numCourses];
for (int i = 0; i < numCourses; i++) {
// 遍历图中的所有节点
traverse(graph, i);
}
// 只要没有循环依赖可以完成所有课程
return !hasCycle;
}
/** 判断图中是否存在环了 */
private void traverse(List<Integer>[] graph, int s) {
if (onPath[s]) {
// 出现环
hasCycle = true;
}
if (visited[s] || hasCycle) {
// 如果已经找到了环,也不用再遍历了
return;
}
// 前序代码位置
visited[s] = true;
onPath[s] = true;
for (int t : graph[s]) {
traverse(graph, t);
}
// 后序代码位置
onPath[s] = false;
}
/** 建图函数 */
private List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
// 图中共有 numCourses 个节点
List<Integer>[] graph = new LinkedList[numCourses];
for (int i = 0; i < numCourses; i++) {
graph[i] = new LinkedList<>();
}
for (int[] edge : prerequisites) {
int from = edge[1], to = edge[0];
// 添加一条从 from 指向 to 的有向边
// 边的方向是「被依赖」关系,即修完课程 from 才能修课程 to
graph[from].add(to);
}
return graph;
}
}
拓扑排序算法(DFS)
拓扑排序(Topological Sorting)直观地说就是,让你把一幅图「拉平」,而且这个「拉平」的图里面,所有箭头方向都是一致的,比如上图所有箭头都是朝右的。
很显然,如果一幅有向图中存在环,是无法进行拓扑排序的,因为肯定做不到所有箭头方向一致;反过来,如果一幅图是「有向无环图」,那么一定可以进行拓扑排序。
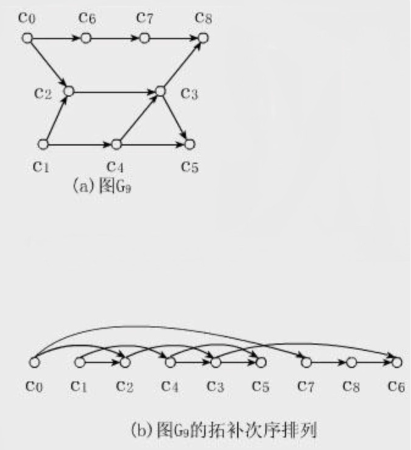
其实也不难看出来,如果把课程抽象成节点,课程之间的依赖关系抽象成有向边,那么这幅图的拓扑排序结果就是上课顺序
如何进行拓扑排序?
将后序遍历的结果进行反转,就是拓扑排序的结果
210. 课程表 II
现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中 prerequisites[i] = [ai, bi] ,表示在选修课程 ai 前 必须 先选修 bi 。
- 例如,想要学习课程
0,你需要先完成课程1,我们用一个匹配来表示:[0,1]。
返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回 任意一种 就可以了。如果不可能完成所有课程,返回 一个空数组 。
class Solution {
// 记录后序遍历结果
List<Integer> postorder = new ArrayList<>();
// 记录是否存在环
boolean hasCycle = false;
boolean[] visited, onPath;
// 主函数
public int[] findOrder(int numCourses, int[][] prerequisites) {
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
visited = new boolean[numCourses];
onPath = new boolean[numCourses];
// 遍历图
for (int i = 0; i < numCourses; i++) {
traverse(graph, i);
}
// 有环图无法进行拓扑排序
if (hasCycle) {
return new int[]{};
}
// 逆后序遍历结果即为拓扑排序结果
Collections.reverse(postorder);
int[] res = new int[numCourses];
for (int i = 0; i < numCourses; i++) {
res[i] = postorder.get(i);
}
return res;
}
// 图遍历函数
void traverse(List<Integer>[] graph, int s) {
if (onPath[s]) {
// 发现环
hasCycle = true;
}
if (visited[s] || hasCycle) {
return;
}
// 前序遍历位置
onPath[s] = true;
visited[s] = true;
for (int t : graph[s]) {
traverse(graph, t);
}
// 后序遍历位置
postorder.add(s);
onPath[s] = false;
}
// 建图函数
List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
// 图中共有 numCourses 个节点
List<Integer>[] graph = new LinkedList[numCourses];
for (int i = 0; i < numCourses; i++) {
graph[i] = new LinkedList<>();
}
for (int[] edge : prerequisites) {
int from = edge[1], to = edge[0];
// 添加一条从 from 指向 to 的有向边
// 边的方向是「被依赖」关系,即修完课程 from 才能修课程 to
graph[from].add(to);
}
return graph;
}
}
说一下为什么要把后序遍历的结果再反转?网上看到的拓扑排序算法不用对后序遍历结果进行反转,这是为什么呢?
原因是他建图的时候对边的定义和我不同。我建的图中箭头方向是「被依赖」关系,比如节点 1 指向 2,含义是节点 1 被节点 2 依赖,即做完 1 才能去做 2,如果你反过来,把有向边定义为「依赖」关系,那么整幅图中边全部反转,就可以不对后序遍历结果反转。具体来说,就是把我的解法代码中 graph[from].add(to); 改成 graph[to].add(from); 就可以不反转了。
把二叉树理解成一幅有向图,边的方向是由父节点指向子节点
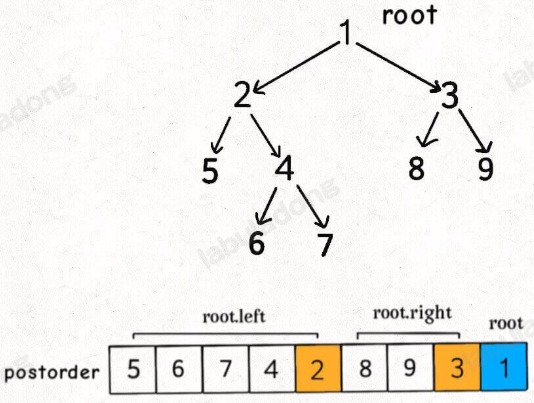
按照我们的定义,边的含义是「被依赖」关系,那么上图的拓扑排序应该首先是节点 1,然后是 2, 3,以此类推
但显然标准的后序遍历结果不满足拓扑排序,而如果把后序遍历结果反转,就是拓扑排序结果了:
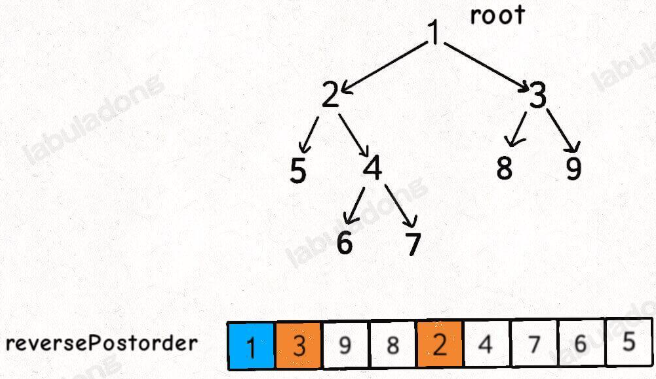
环检测算法(BFS)
// 主函数
public boolean canFinish(int numCourses, int[][] prerequisites) {
// 建图,有向边代表「被依赖」关系
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
// 构建入度数组
int[] indegree = new int[numCourses];
for (int[] edge : prerequisites) {
int from = edge[1], to = edge[0];
// 节点 to 的入度加一
indegree[to]++;
}
// 根据入度初始化队列中的节点
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < numCourses; i++) {
if (indegree[i] == 0) {
// 节点 i 没有入度,即没有依赖的节点
// 可以作为拓扑排序的起点,加入队列
q.offer(i);
}
}
// 记录遍历的节点个数
int count = 0;
// 开始执行 BFS 循环
while (!q.isEmpty()) {
// 弹出节点 cur,并将它指向的节点的入度减一
int cur = q.poll();
count++;
for (int next : graph[cur]) {
indegree[next]--;
if (indegree[next] == 0) {
// 如果入度变为 0,说明 next 依赖的节点都已被遍历
q.offer(next);
}
}
}
// 如果所有节点都被遍历过,说明不成环
return count == numCourses;
}
/** 建图函数 */
private List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
// 图中共有 numCourses 个节点
List<Integer>[] graph = new LinkedList[numCourses];
for (int i = 0; i < numCourses; i++) {
graph[i] = new LinkedList<>();
}
for (int[] edge : prerequisites) {
int from = edge[1], to = edge[0];
// 添加一条从 from 指向 to 的有向边
// 边的方向是「被依赖」关系,即修完课程 from 才能修课程 to
graph[from].add(to);
}
return graph;
}
总结下这段 BFS 算法的思路:
1、构建邻接表,和之前一样,边的方向表示「被依赖」关系。
2、构建一个 indegree 数组记录每个节点的入度,即 indegree[i] 记录节点 i 的入度。
3、对 BFS 队列进行初始化,将入度为 0 的节点首先装入队列。
4、开始执行 BFS 循环,不断弹出队列中的节点,减少相邻节点的入度,并将入度变为 0 的节点加入队列。
5、如果最终所有节点都被遍历过(count 等于节点数),则说明不存在环,反之则说明存在环。
所有节点都被遍历过一遍,也就说明图中不存在环。
反过来说,如果按照上述逻辑执行 BFS 算法,存在节点没有被遍历,则说明成环。
比如下面这种情况,队列中最初只有一个入度为 0 的节点:
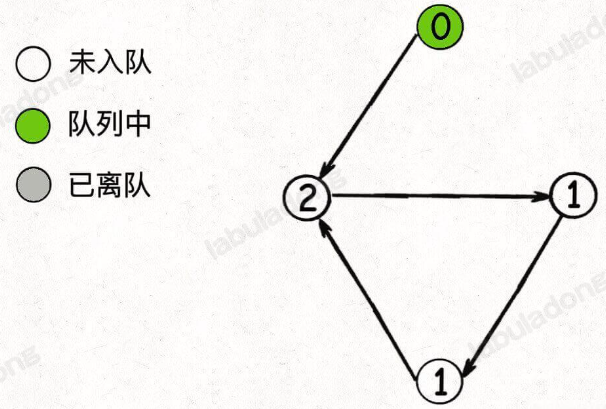
当弹出这个节点并减小相邻节点的入度之后队列为空,但并没有产生新的入度为 0 的节点加入队列,所以 BFS 算法终止
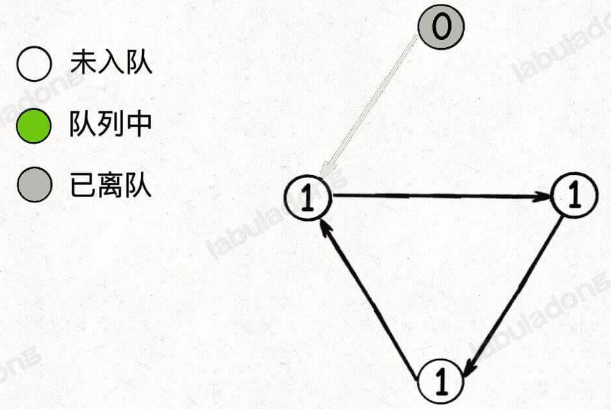
你看,如果存在节点没有被遍历,那么说明图中存在环
拓扑排序算法(BFS)
// 主函数
public int[] findOrder(int numCourses, int[][] prerequisites) {
// 建图,和环检测算法相同
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
// 计算入度,和环检测算法相同
int[] indegree = new int[numCourses];
for (int[] edge : prerequisites) {
int from = edge[1], to = edge[0];
indegree[to]++;
}
// 根据入度初始化队列中的节点,和环检测算法相同
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < numCourses; i++) {
if (indegree[i] == 0) {
q.offer(i);
}
}
// 记录拓扑排序结果
int[] res = new int[numCourses];
// 记录遍历节点的顺序(索引)
int count = 0;
// 开始执行 BFS 算法
while (!q.isEmpty()) {
int cur = q.poll();
// 弹出节点的顺序即为拓扑排序结果
res[count] = cur;
count++;
for (int next : graph[cur]) {
indegree[next]--;
if (indegree[next] == 0) {
q.offer(next);
}
}
}
if (count != numCourses) {
// 存在环,拓扑排序不存在
return new int[]{};
}
return res;
}
/** 建图函数 */
private List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
// 图中共有 numCourses 个节点
List<Integer>[] graph = new LinkedList[numCourses];
for (int i = 0; i < numCourses; i++) {
graph[i] = new LinkedList<>();
}
for (int[] edge : prerequisites) {
int from = edge[1], to = edge[0];
// 添加一条从 from 指向 to 的有向边
// 边的方向是「被依赖」关系,即修完课程 from 才能修课程 to
graph[from].add(to);
}
return graph;
}
–end–