1.什么是GBDT算法
GBDT(Gradient Boosting Decision Tree),全名叫梯度提升决策树,是一种迭代的决策树算法,又叫 MART(Multiple Additive Regression Tree),它通过构造一组弱的学习器(树),并把多棵决策树的结果累加起来作为最终的预测输出。该算法将决策树与集成思想进行了有效的结合。
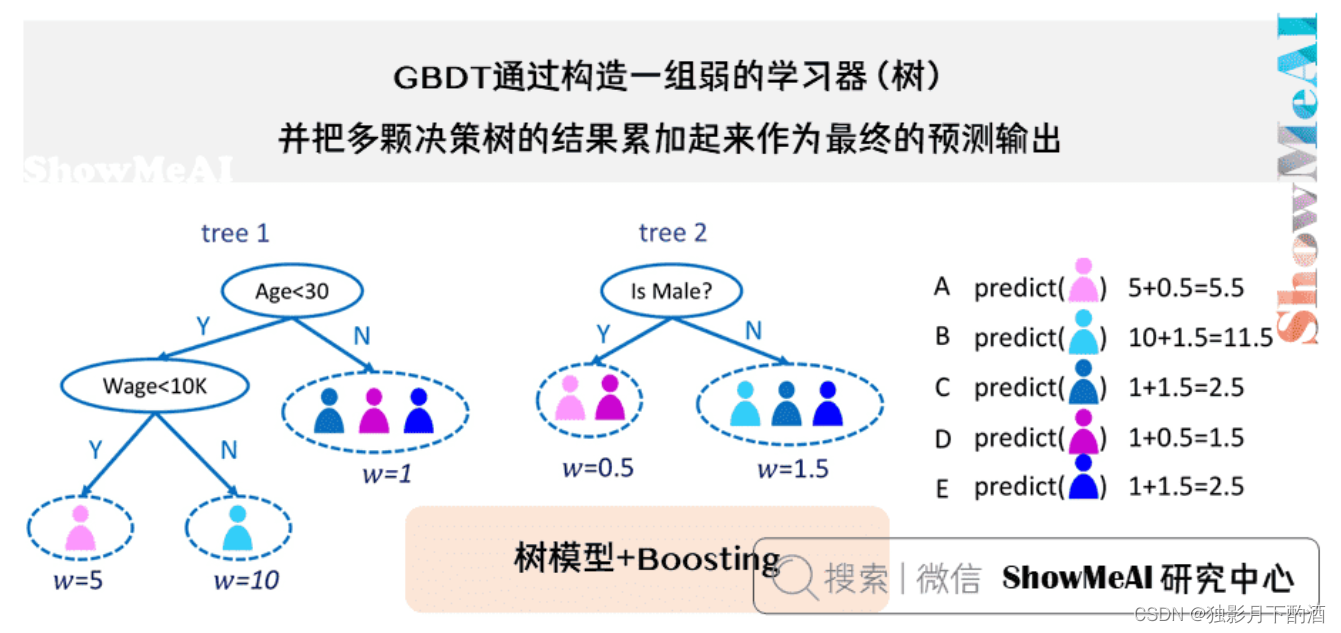
GBDT主要由三个概念组成:Regression Decistion Tree(即DT),Gradient Boosting(即GB),Shrinkage (算法的一个重要演进分枝,目前大部分源码都按该版本实现)。
- DT:GBDT中的树都是回归树,不是分类树;将所有树的结果累加起来作为最终的结果。
- GB:沿着梯度方向,构造一系列的弱分类器函数,并以一定的权重组合起来,形成最终决策的强分类器。
- Shrinkage:每次走一小步逐渐逼近结果,要比每次迈一大步很快逼近结果的方式更容易避免过拟合。
2.Boosting核心思想
Boosting方法训练基分类器时采用串行的方式,各个基分类器之间有依赖。它的基本思路是将基分类器(过拟合)层层叠加,每一层在训练的时候,对前一层基分类器分错的样本,给予更高的权重。测试时,根据各层分类器的结果的加权得到最终结果。
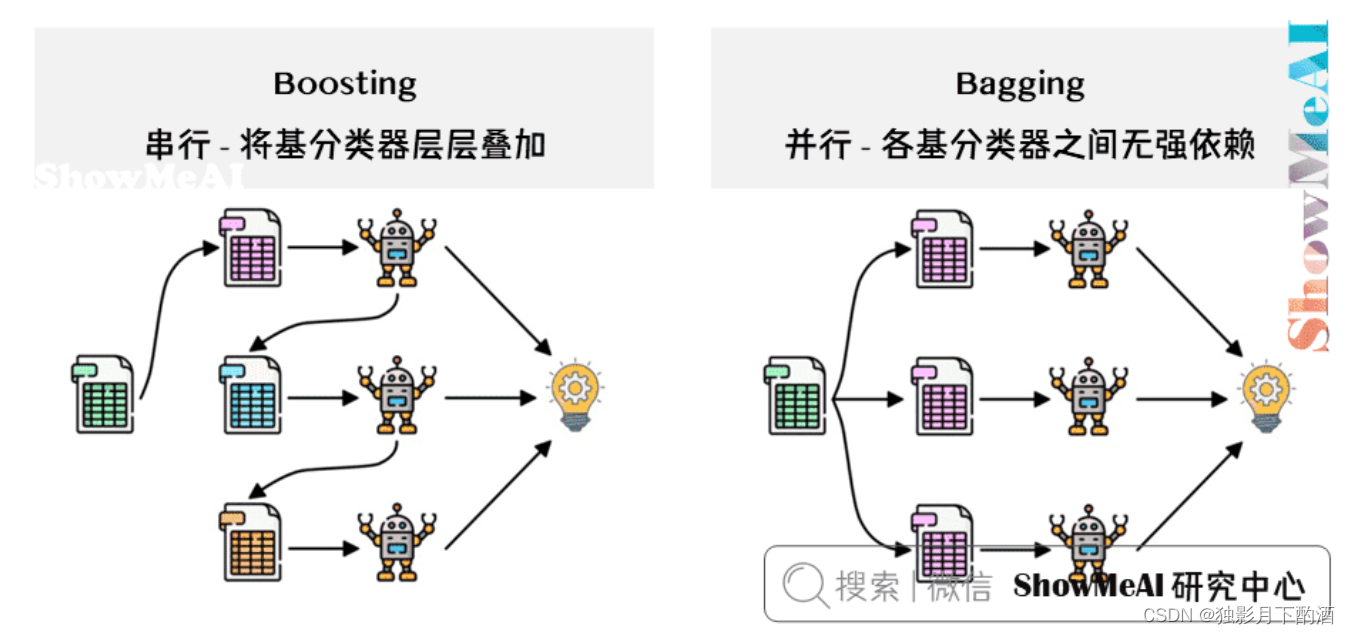
Bagging 与 Boosting 的串行训练方式不同,Bagging 方法在训练过程中,各基分类器(欠拟合)之间无强依赖,可以进行并行训练。
3.GBDT原理详解
- 所有弱分类器的结果相加等于预测值。
- 每次都以当前预测为基准,下一个弱分类器去拟合误差函数对预测值的残差(预测值与真实值之间的误差)。
- GBDT的弱分类器使用的是树模型。
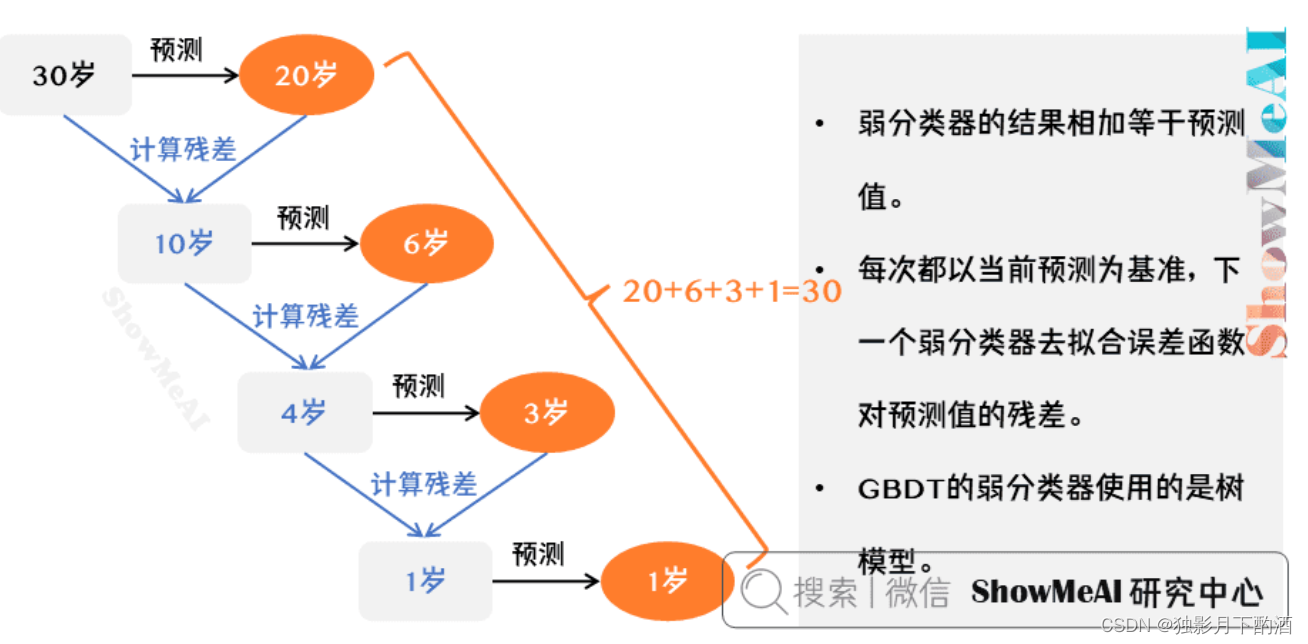
上图是一个非常简单帮助理解的示例,用 GBDT 去预测年龄:
- 第一个弱分类器(第一棵树)预测一个年龄(如 20 20 20 岁),计算发现误差有 10 10 10 岁;
- 第二棵树预测拟合残差,预测值 ,计算发现差距还有 4 4 4 岁;
- 第三棵树继续预测拟合残差,预测值 3 3 3,发现差距只有 1 1 1 岁了;
- 第四课树用 1 1 1 岁拟合剩下的残差,完成。
最终,四棵树的结论加起来,得到 30 30 30 岁这个标注答案(实际工程实现里,GBDT 是计算负梯度,用负梯度近似残差)。
3.1 GBDT与负梯度近似残差
回归任务下,GBDT在每一轮的迭代时对每个样本都会有一个预测值,此时的损失函数为均方差损失函数:
l
(
y
i
,
y
^
i
)
=
1
2
(
y
i
−
y
^
i
)
2
l(y_i,\hat y_i) = \frac{1}{2}(y_i-\hat y_i)^2
l(yi,y^i)=21(yi−y^i)2
损失函数的负梯度计算如下:
−
[
∂
l
(
y
i
−
y
^
i
)
∂
y
^
i
]
=
(
y
i
−
y
^
i
)
-[\frac{\partial l(y_i-\hat y_i)}{\partial\hat y_i}]=(y_i-\hat y_i)
−[∂y^i∂l(yi−y^i)]=(yi−y^i)

可以看出,当损失函数选用「均方误差损失」时,每一次拟合的值就是(真实值-预测值),即残差。
3.2 GBDT训练过程
假定训练集只有 4 4 4 个人 ( A , B , C , D ) (A,B,C,D) (A,B,C,D),他们的年龄分别是 ( 14 , 16 , 24 , 26 ) (14,16,24,26) (14,16,24,26)。其中 A 、 B A、B A、B 分别是高一和高三学生;$ C、D$ 分别是应届毕业生和工作两年的员工。
先看看用回归树来训练,得到的结果如下图所示:
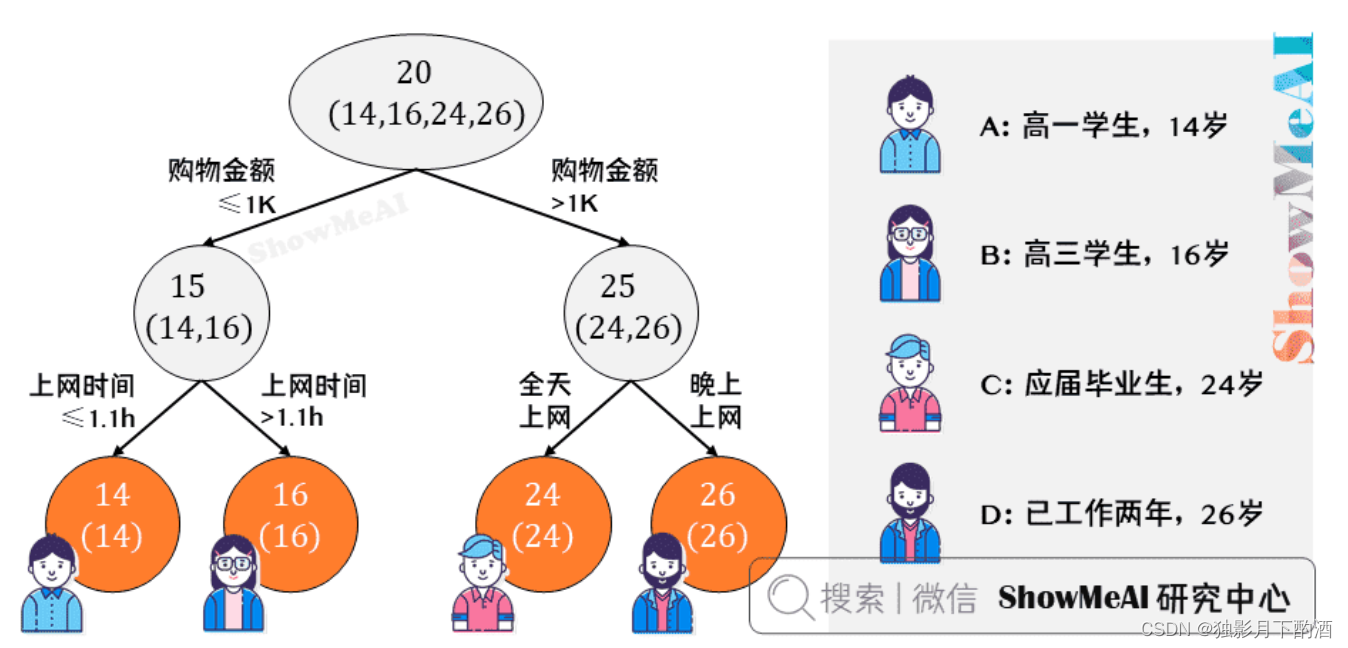
接下来使用GBDT训练,由于样本数据少,我们限定叶子节点最多为 2 2 2 (即每棵树都只有一个分枝),并且限定树的棵树为 2 2 2。最终训练得到的结果如下图所示:
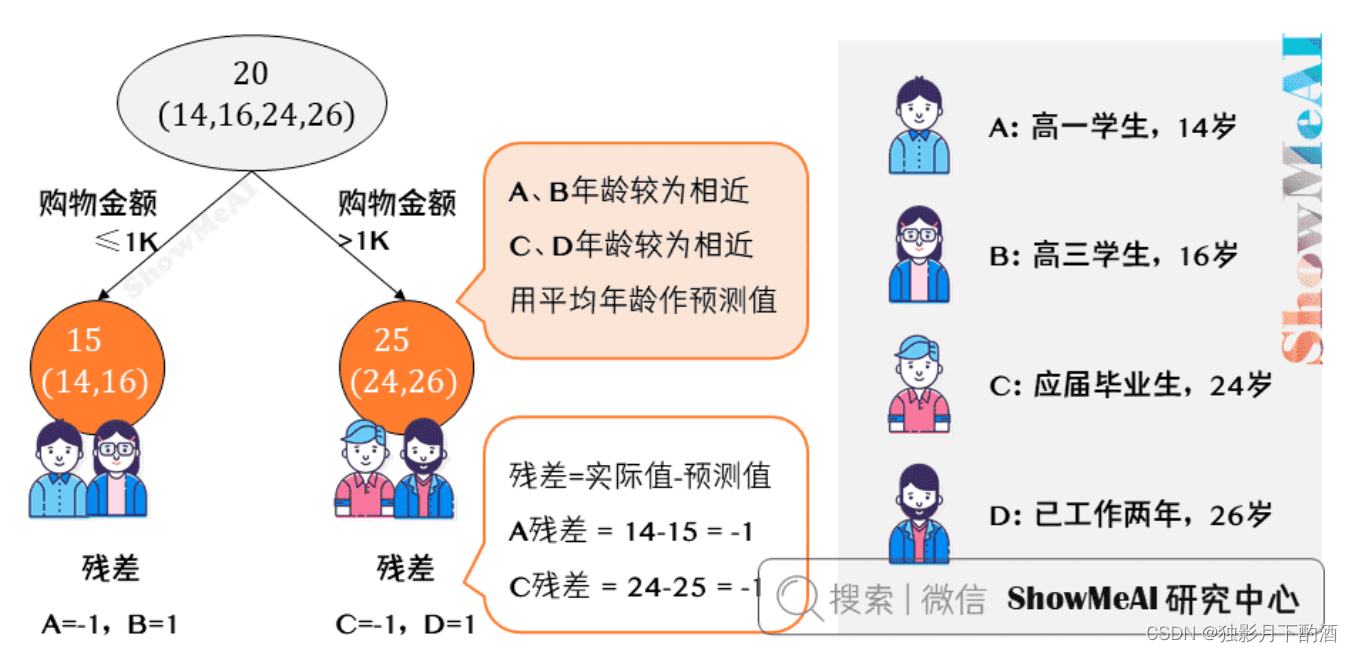
从上图可知: A 、 B A、B A、B年龄较为相近, C 、 D C、D C、D年龄较为相近,被分为左右两支,每支用平均年龄作为预测值。
- 计算残差(即「实际值」-「预测值」),所以 A A A 的残差 14 − 15 = − 1 14-15=-1 14−15=−1。
- 这里 A A A 的「预测值」是指前面所有树预测结果累加的和,在当前情形下前序只有一棵树,所以直接是 15 15 15,其他多树的复杂场景下需要累加计算作为 A A A 的预测值
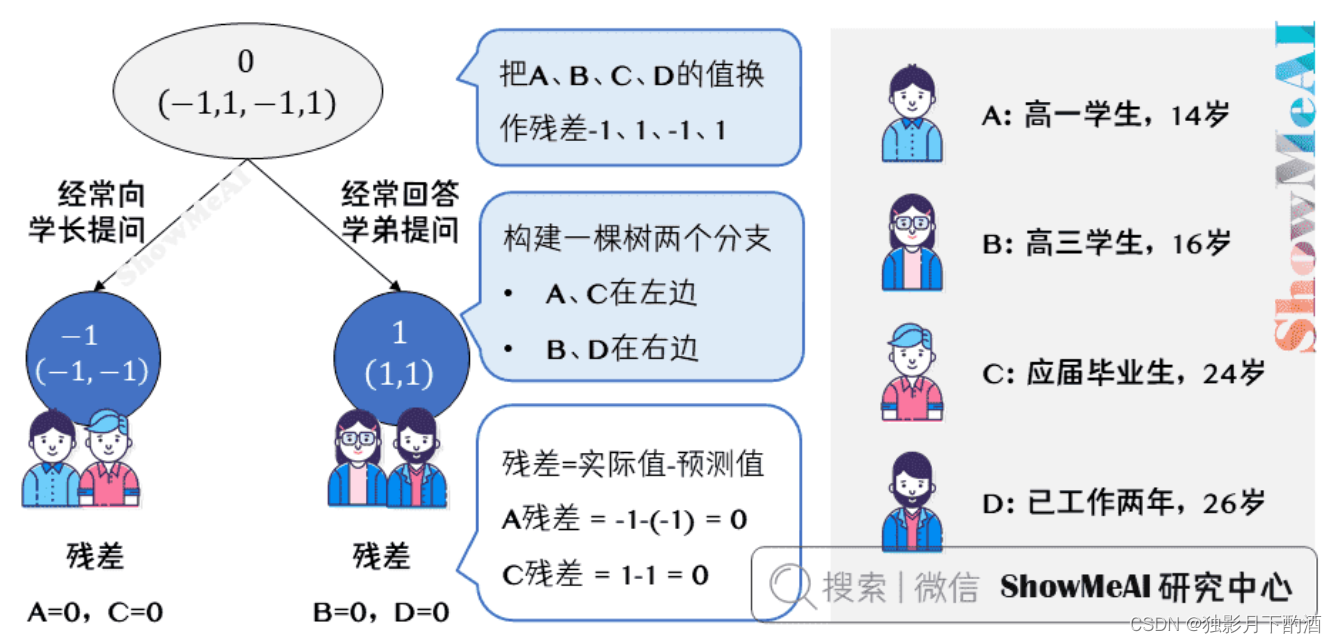
上图中的树就是残差学习的过程了:
- 把 A 、 B 、 C 、 D A、B、C、D A、B、C、D的值换作残差 − 1 、 1 、 − 1 、 1 -1、1、-1、1 −1、1、−1、1,再构建一棵树学习,这棵树只有两个值 1 1 1 和 − 1 -1 −1,直接分成两个节点: A 、 C A、C A、C 在左边, B 、 D B、D B、D 在右边。
- 这棵树学习残差,在我们当前这个简单的场景下,已经能保证预测值和实际值(上一轮残差)相等了。
- 我们把这棵树的预测值累加到第一棵树上的预测结果上,就能得到真实年龄,这个简单例子中每个人都完美匹配,得到了真实的预测值。
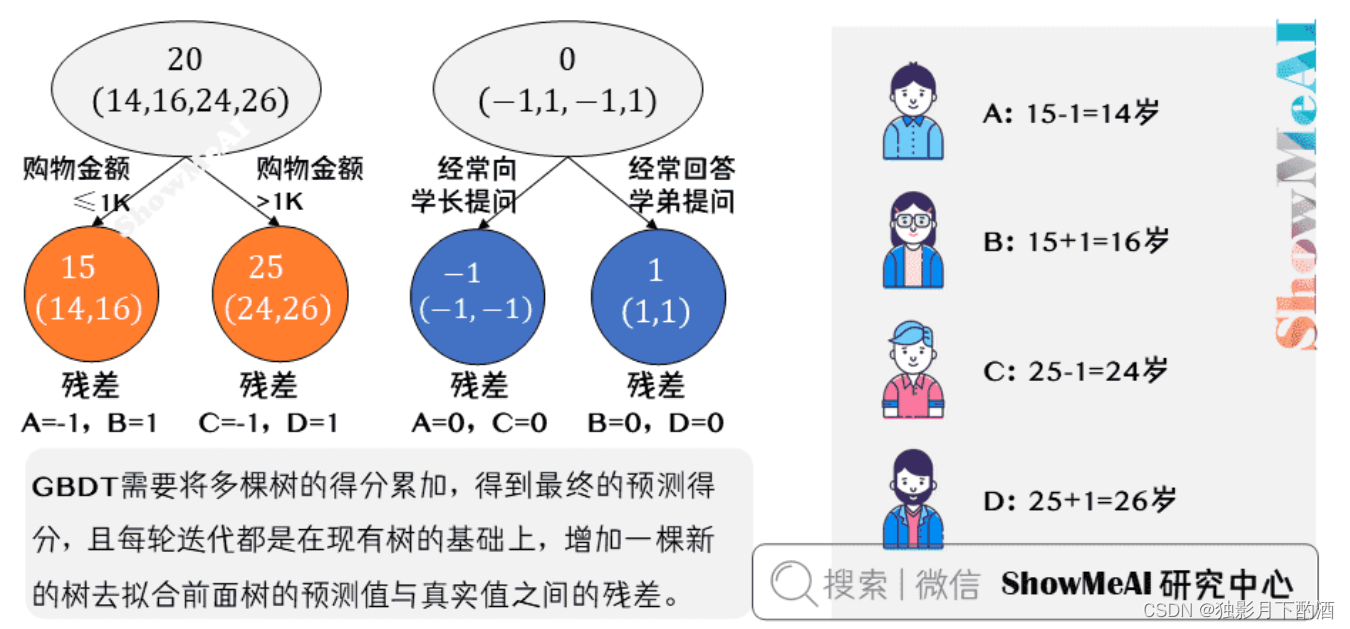
最终的预测过程是这样的:
A A A: 14 14 14 岁高一学生,购物较少,经常问学长问题;预测年龄 A = 15 – 1 = 14 A = 15 – 1 = 14 A=15–1=14
B B B: 16 16 16 岁高三学生;购物较少,经常被学弟问问题;预测年龄 B = 15 + 1 = 16 B = 15 + 1 = 16 B=15+1=16
C C C: 24 24 24 岁应届毕业生;购物较多,经常问师兄问题;预测年龄 C = 25 – 1 = 24 C = 25 – 1 = 24 C=25–1=24
D D D: 26 26 26 岁工作两年员工;购物较多,经常被师弟问问题;预测年龄 D = 25 + 1 = 26 D = 25 + 1 = 26 D=25+1=26
综上,GBDT 需要将多棵树的得分累加得到最终的预测得分,且每轮迭代,都是在现有树的基础上,增加一棵新的树去拟合前面树的预测值与真实值之间的残差。
3.3 思考
Q:回归树与GBDT得到的结果是相同的,那么为啥还要使用GBDT?
答:防止模型过拟合
在训练精度和实际精度(或测试精度)之间,后者才是我们想要真正得到的。
在上述的实例中,回归树算法为了达到 100 % 100\% 100% 精度使用了 3 3 3 个 feature(上网时长、时段、网购金额),其中分枝“上网时长 > 1.1 h 1.1h 1.1h ” 很显然已经过拟合了,在这个数据集上 A , B A,B A,B 也许恰好 A A A 每天上网 1.09 h 1.09h 1.09h , B B B 上网 1.05 h 1.05h 1.05h,但用上网时间是不是 > 1.1 h 1.1h 1.1h 来判断所有人的年龄很显然是有悖常识的。而GBDT算法只用了 2 2 2 个feature就搞定了,后一个feature是问答比例,显然GBDT算法更靠谱。Boosting的最大好处在于,每一步的残差计算其实变相地增大了分错instance的权重,而已经分对的instance则都趋向于 0 0 0。这样后面的树就能越来越专注那些前面被分错的instance。
4.梯度提升 vs 梯度下降
对比一下「梯度提升」与「梯度下降」。这两种迭代优化算法,都是在每1轮迭代中,利用损失函数负梯度方向的信息,更新当前模型,只不过:
- 梯度下降中,模型是以参数化形式表示,从而模型的更新等价于参数的更新。
w t = w t − 1 − ρ t ∇ w L ∣ w = w t − 1 L = ∑ i l ( y i , f w ( w i ) ) w_t=w_{t-1}-\rho_t\nabla_wL|_{w=w_{t-1}} \\[2ex] L= \sum \limits_il(y_i,f_w(w_i)) wt=wt−1−ρt∇wL∣w=wt−1L=i∑l(yi,fw(wi))
- 梯度提升中,模型并不需要进行参数化表示,而是直接定义在函数空间中,从而大大扩展了可以使用的模型种类。
F t = F t − 1 − ρ t ∇ F L ∣ F = F t − 1 L = ∑ i l ( y i , F ( x i ) ) F_t=F_{t-1}-\rho_t\nabla_FL|_{F=F_{t-1}} \\[2ex] L= \sum \limits_il(y_i,F(x_i)) Ft=Ft−1−ρt∇FL∣F=Ft−1L=i∑l(yi,F(xi))
4.1 GBDT中的梯度
基于Boosting的集成学习是通过一系列的弱学习器,进而通过不同的组合策略得到相应的强学习器。在GBDT的迭代中,假设前一轮的得到的强学习器为 f t − 1 ( x ) f_{t-1}(x) ft−1(x),对应的损失函数则为 L ( y , f t − 1 ( x ) ) L(y, f_{t-1}(x)) L(y,ft−1(x))。因此在新一轮迭代的目的就是找到了一个弱学习器 h t ( x ) h_t(x) ht(x),使得损失函数 L ( y , f t − 1 ( x ) + h t ( x ) ) L(y, f_{t-1}(x)+h_t(x)) L(y,ft−1(x)+ht(x))达到最小。难点在于损失函数如何度量?
梯度提升算法:利用最速下降的近似方法,即利用损失函数的负梯度在当前模型的值,作为回归问题中提升树算法的残差的近似值,拟合一个回归树。第 t t t 轮的第 i i i 个样本的负梯度表示为: r t i = − [ ∂ L ( y i , f ( x i ) ) ∂ f ( x i ) ] f ( x ) = f t − 1 ( x ) r_{ti}=-\left[\frac{\partial L(y_i,f(x_i))}{\partial f(x_i)}\right]_{f(x)=f_{t-1}(x)} rti=−[∂f(xi)∂L(yi,f(xi))]f(x)=ft−1(x)
4.2 GBDT回归算法基本流程
输入: 训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . ( x N , y N ) } , x i ∈ X ⊆ R n , y i ∈ Y ⊆ R , i = 1 , 2 , . . , N T=\{(x_1,y_1),(x_2,y_2),...(x_N,y_N)\},x_i \in \mathcal X \subseteq R^n,y_i \in \mathcal Y \subseteq R,i=1,2,..,N T={(x1,y1),(x2,y2),...(xN,yN)},xi∈X⊆Rn,yi∈Y⊆R,i=1,2,..,N,最大迭代次数 M M M ,损失函数 L ( y i , f ( x i ) ) L(y_i,f(x_i)) L(yi,f(xi))
输出: 回归树 f ^ ( x ) \hat f\left(x\right) f^(x)
1.初始化 f 0 ( x ) = a r g min c ∑ i = 1 N L ( y i , c ) f_0(x)= arg \min\limits_c\sum\limits_{i=1}\limits^{N}L(y_i,c) f0(x)=argcmini=1∑NL(yi,c)
2.For m = 1 m=1 m=1 to M M M:
2.1 For i = 1 i=1 i=1 to N N N compute: r m i = − [ ∂ L ( y i , f ( x i ) ) ∂ f ( x i ) ] f ( x ) = f m − 1 ( x ) r_{mi}=-\left[\frac{\partial L(y_i,f(x_i))}{\partial f(x_i)}\right]_{f(x)=f_{m-1}(x)} rmi=−[∂f(xi)∂L(yi,f(xi))]f(x)=fm−1(x)
2.2 对 r m i r_{mi} rmi 拟合回归树,得到第 m m m 棵树的叶子结点区域 R m j , j = 1 , 2 , . . . , J m R_{mj},j=1,2,...,J_m Rmj,j=1,2,...,Jm
2.3 For j = 1 j=1 j=1 to J m J_m Jm compute: c m j = a r g min c ∑ x i ∈ R m j L ( y i , f t − 1 ( x i ) + c ) c_{mj}=arg \min\limits_c\sum\limits_{x_i \in R_{mj}}L(y_i,f_{t-1}(x_i)+c) cmj=argcminxi∈Rmj∑L(yi,ft−1(xi)+c)
2.4 更新 f m ( x ) = f m − 1 ( x ) + ∑ j = 1 J m c m j I ( x ∈ R m j ) f_m(x)=f_{m-1}(x)+\sum\limits_{j=1}\limits^{J_m}c_{mj}I(x\in R_{mj}) fm(x)=fm−1(x)+j=1∑JmcmjI(x∈Rmj)
3.输出回归树: f ^ ( x ) = f M ( x ) \hat f(x)=f_M(x) f^(x)=fM(x)
5.GBDT优缺点
5.1 优点
- 预测阶段,因为每棵树的结构都已确定,可并行化计算,计算速度快。
- 适用稠密数据,泛化能力和表达能力都不错,数据科学竞赛榜首常见模型。
- 可解释性不错,鲁棒性亦可,能够自动发现特征间的高阶关系。
5.2 缺点
- GBDT 在高维稀疏的数据集上,效率较差,且效果表现不如 SVM 或神经网络。
- 适合数值型特征,在 NLP 或文本特征上表现弱。
- 训练过程无法并行,工程加速只能体现在单棵树构建过程中。
6.随机森林 vs GBDT
6.1 相同点
- 都是集成模型,由多棵树组构成,最终的结果都是由多棵树一起决定。
- RF 和 GBDT 在使用 CART 树时,可以是分类树或者回归树。
6.2 不同点
- 训练过程中,随机森林的树可以并行生成,而 GBDT 只能串行生成。
- 随机森林的结果是多数表决表决的,而 GBDT 则是多棵树累加之。
- 随机森林对异常值不敏感,而 GBDT 对异常值比较敏感。
- 随机森林降低模型的方差,而 GBDT 是降低模型的偏差。
7.GBDT实践
7.1 数据说明
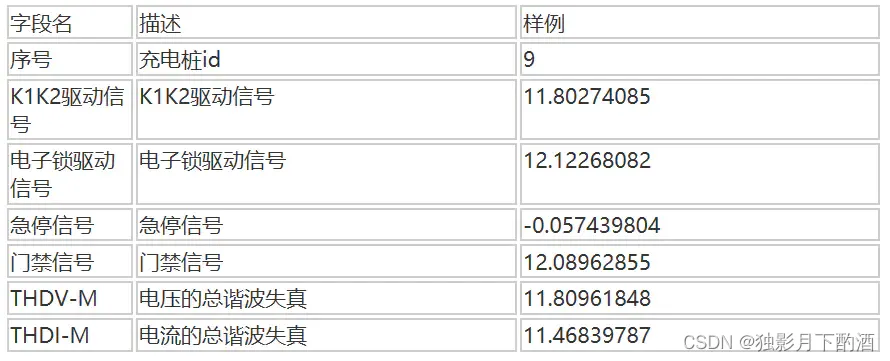
新能源汽车充电桩的故障检测问题,提供 85500 85500 85500 条训练数据(标签: 0 0 0 代表充电桩正常, 1 1 1 代表充电桩有故障),参赛者需对 36644 36644 36644 条测试数据进行预测。
7.2 数据
训练数据: data_train.csv
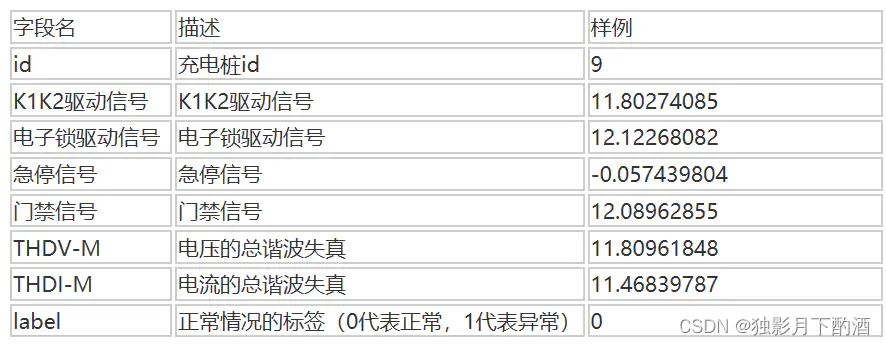
测试数据:data_test.csv
7.3 代码实现
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingClassifier
import joblib
# 读取数据
data = pd.read_csv(r"./data/data_train.csv", sep=',' )
# ['K1K2驱动信号','电子锁驱动信号','急停信号','门禁信号','THDV-M','THDI-M']
x_columns = []
# 读取文件,去除id和label标签项,并把数据分成训练集和验证集
for x in data.columns:
if x not in ['id', 'label']:
x_columns.append(x)
X = data[x_columns]
y = data['label']
# 采用默认划分比例,即75%数据作为训练集,25%作为预测集。
x_train, x_test, y_train, y_test = train_test_split(X, y)
# 模型训练,使用GBDT算法
gbr = GradientBoostingClassifier(n_estimators=3000, max_depth=2, min_samples_split=2, learning_rate=0.1)
gbr.fit(x_train, y_train.ravel())
joblib.dump(gbr, './model/train_model_result4.m') # 保存模型
y_gbr = gbr.predict(x_train)
y_gbr1 = gbr.predict(x_test)
acc_train = gbr.score(x_train, y_train)
acc_test = gbr.score(x_test, y_test)
print(acc_train)
print(acc_test)
模型预测
# -*- coding: utf-8 -*-
import numpy as np
import pandas as pd
import joblib
# 加载模型并预测
gbr = joblib.load('./model/train_model_result4.m') # 加载模型
test_data = pd.read_csv(r"./data/data_test.csv")
testx_columns = []
for xx in test_data.columns:
if xx not in ['id', 'label']:
testx_columns.append(xx)
test_x = test_data[testx_columns]
test_y = gbr.predict(test_x)
test_y = np.reshape(test_y, (36644, 1))
# 保存预测结果
df = pd.DataFrame()
df['id'] = test_data['id']
df['label'] = test_y
df.to_csv("./result/data_predict.csv", header=None, index=False)
8.总结
- GBDT是一种基于Boosting思想的迭代决策树算法,通过构造一组弱的学习器(树),并把多棵决策树的结果累加起来作为最终的预测输出。该算法将决策树与集成思想进行了有效的结合。
- 集成学习Boosting(降低偏差)和Bagging(降低方差)的理解以及区别。
- GBDT算法的思想:所有弱分类器的结果相加等于预测值;每次都以当前预测为基准,下一个弱分类器去拟合误差函数对预测值的残差(预测值与真实值之间的误差)。
- GBDT的理解:残差(每棵树学习的都是前一棵树的残差-全局最优)和梯度(每一棵回归树通过梯度下降法学习之前输的梯度下降值–局部最优)
本文仅仅作为个人学习记录所用,不作为商业用途,谢谢理解。
参考:
1.https://www.jianshu.com/p/47e73a985ba1
2.https://www.showmeai.tech/tutorials/34?articleId=193