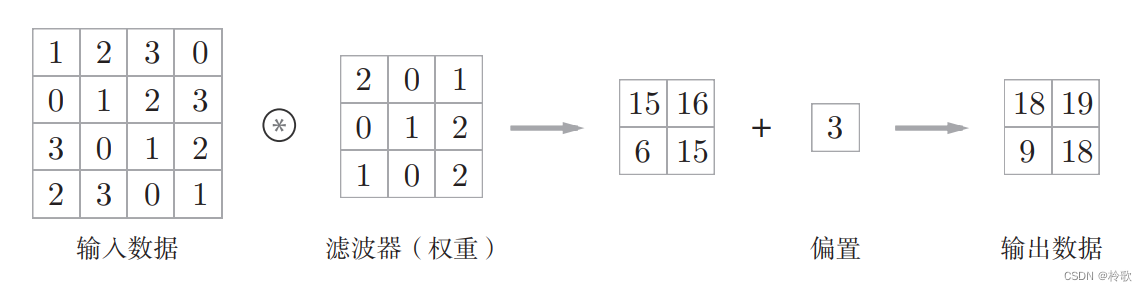
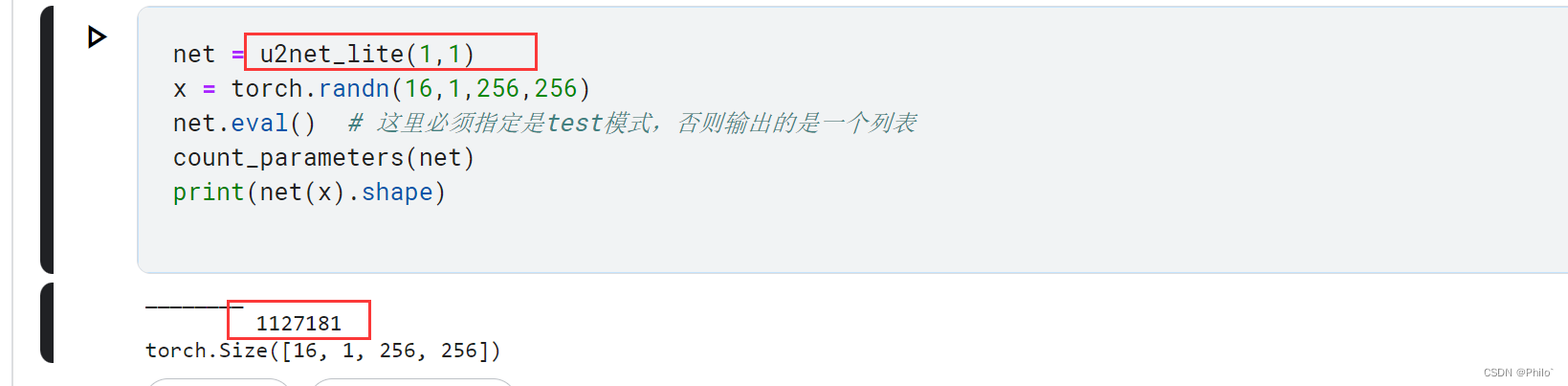
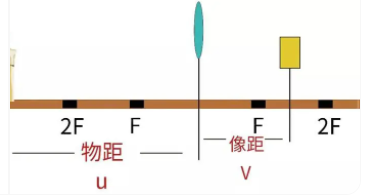
1.原理说明
交互作用(Interaction effect)指两个或多个因素(比如A因素和B因素)对于某项(比如身高)的影响时,A因素和B因素各个水平之间是否存在着相互作用关系。比如A因素为性别,B因素为区域,男性并且北方群体时身高如何,男性并且南方群体时身高如何,也或者女性并且北方群体时身高如何,女性并且南方群体时身高如何。性别的2个水平(男和女),与区域的2个水平(北方和南方)之间有没有交互。
简单言之:身高效应 = 性别 + 区域 + 性别*区域。如果交互项(性别*区域)并不具有显著性,此时说明具有交互效应。
交互效应的分析上,交互项的设置非常关键,其显著性即代表是否存在着交互效应。接下来具体说明交互项设置。
2.交互项设置
第1部分简要阐述交互作用的简要应用,本部分介绍交互项的设置,如下表格说明:
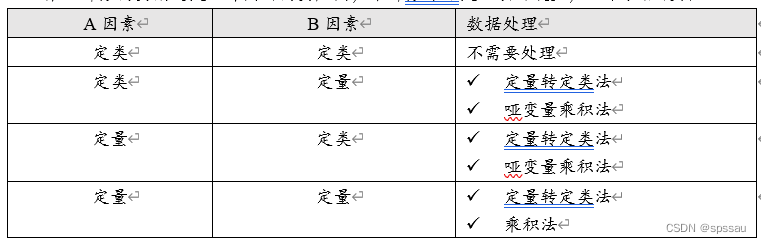
- A定类B定类。此时直接使用SPSSAU的双因素方差进行研究即可,并且选中‘二阶效应’即可,并不需要提前进行交互项设置处理。
- A定类B定量。此时共有两种处理方式,分别是‘定量转定类法’和‘哑变量乘积法’,如下表格说明:

将定量数据转化成定类数据,相当于将定量数据进行分组,变相地变成定类数据,然后使用双因素方差分析时,选中‘二阶效应’即可进行分析。
哑变量乘积法时,将A因素进行哑变量处理,然后将得到的哑变量分别与B因素相乘,即得到交互项,至于后续分析方法,通常是使用ols线性回归。
- A定量B定类。完全参照‘A定类B定量’即可。
- A定量B定量。此时可分别将A或者B进行‘定量转定类法’处理,也或者直接将A乘B得到交互项,至于后续分析方法,通常使用ols线性回归。
3.SPSSAU操作
第2部分中讲述交互项基本原理,接下来讲解SPSSAU操作,分别分为四部分。以及操作时使用数据如下图:
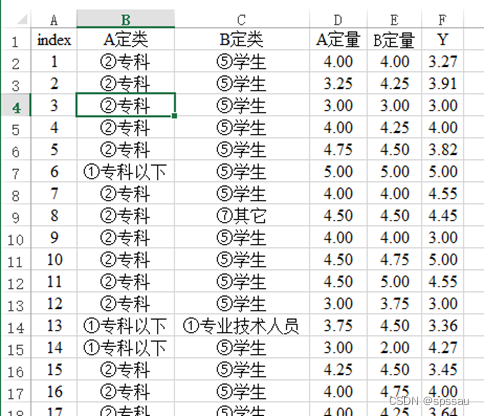
上述案例数据的说明如下表格:
| 项 | 说明 |
| Index | 编号,无特别意义 |
| A定类 | 学历:专科以下、专利等,定类数据 |
| B定类 | 职业:学生、专业技术人员等,定类数据 |
| A定量 | 连续数据 |
| B定量 | 连续数据 |
| Y | 连续数据 |
4.A定类B定类
A和B均为定类数据时,直接使用双因素方差分析,并且选中‘二阶效应’即可,最终通过交互项去判断交互作用。如下图操作:
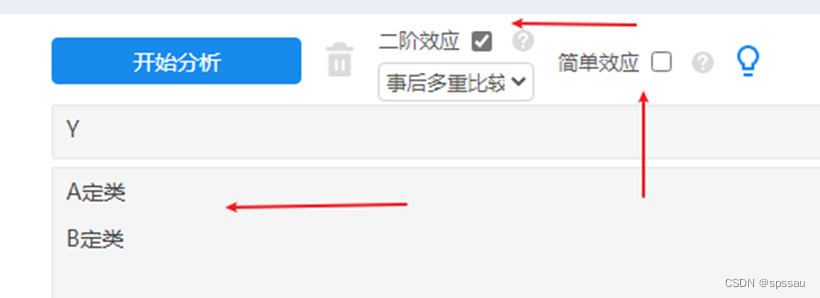
二阶效应事实上就是‘交互作用’,如果有更多复杂的操作需要,可考虑选中‘简单效应’这种更复杂的分析功能。
2.A定类B定量
A定类B定量时,如果希望将B转化为定类数据,此时可使用SPSSAU数据处理->数据编码功能,里面提供范围编码或数字编码等,如下图所示:
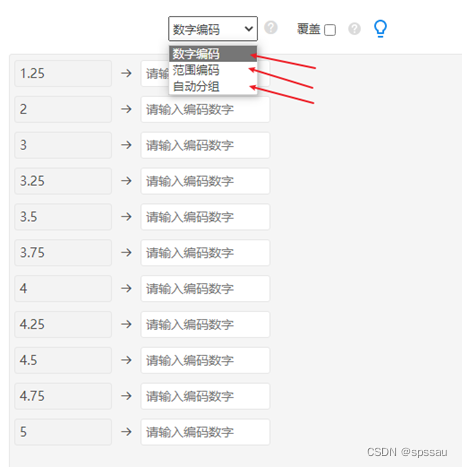
SPSSAU->数据处理->数据编码
数据编码相对简单易懂,暂不赘述。接下来说明‘哑变量乘积法’,其分为两个步骤,第1步是生成哑变量,第2步是乘积。
第1步哑变量设置,如下操作截图:
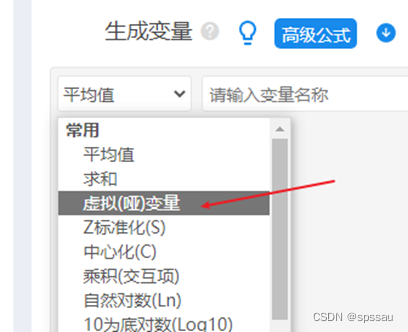
SPSSAU->数据处理->生成变量,处理后得到5个新标题如下图:
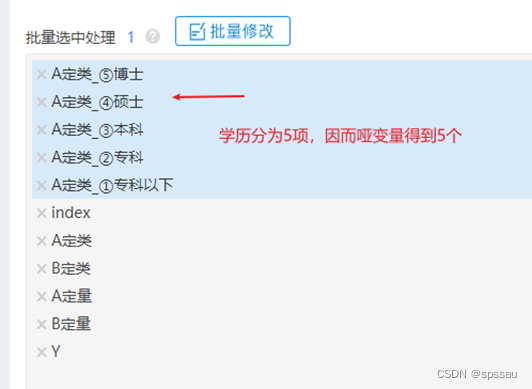
由于学历是5项,因而其会得到5个哑变量,具体原理可参考页面:
第2步乘积,如下操作截图:
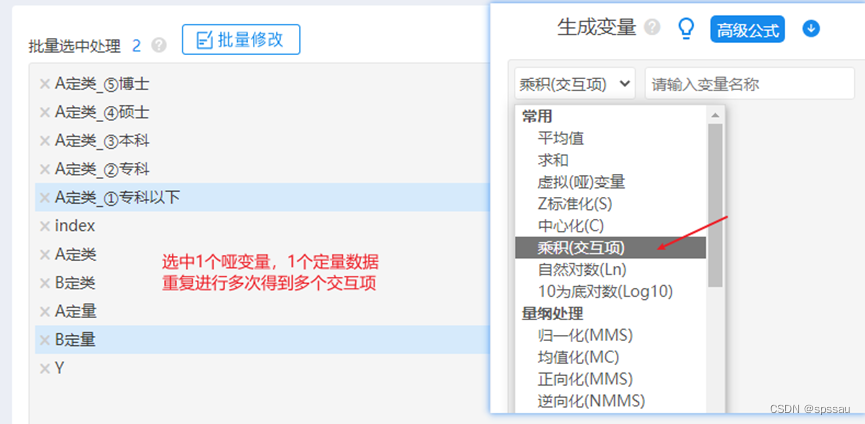
由于有5个哑变量,那么重复进行的话就会有5个交互项,操作如上图。
接着后续进行分析时,切记,有5个哑变量(或5个交互项),以及通常使用ols线性回归进行交互作用分析,那么一定要少放1项(即参照项),至于是少放‘专科以下’,也或者‘博士’,由研究者决定,少放的该项即为参照项。将得到的交互项放入模型中即可,交互项的显著性即可表示是否具有交互效应用。
3.A定量B定类
此部分内容参考3.2进行即可
4.A定量B定量
如果A和B均为定量,可分别将A和B进行转化,设置成定类数据,参考3.2部分进行即可。
如果是直接相乘得到交互项,那么操作如下图,2个定量数据进行相乘得到1个交互项,操作如下图:
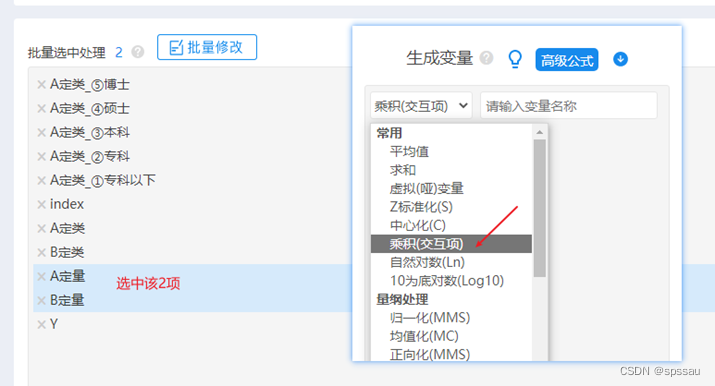
接着后续进行分析时,通常使用ols线性回归进行交互作用分析,将得到的交互项放入模型中即可,交互项的显著性即可表示是否具有交互效应用。