写在前面
此篇文章是在网络上搜集的题目,每一题都可能出现错误,如果各位大佬发现了错误,请在评论区回复一下,看到了就会改
树
根据遍历序列,画树,求另外一种遍历序列
以下中序遍历简称为中序,其他的同理,另外形如中序(xxx),我所要表达的意思是,暂时只看中序中的xxx部分,
例题一 根据中序,后序求先序
已知二叉树的中序遍历序列为DBEAFHCG,后序遍历序列为DEBHFGCA,构造二叉树,写出先序遍历序列
就一句话,从中序遍历中区分左右子树,从后序遍历序列中找根节点
下面是详细的
- 从后序遍历序列中可以得到根节点(就是最后一个):A
- DEB在左子树上面,且B是左子树的根节点;HFGC在右子树上面,且右子树的根节点是C
- B是左子树的根节点,由中序遍历(DBE)可得,B的左孩子为D,B的右孩子为E;由中序遍历(FHCG)可得,C的右孩子为G,C的左子树上必有FH
- 从后序遍历HF中可得,F是根节点,由中序遍历可得F得右孩子是H
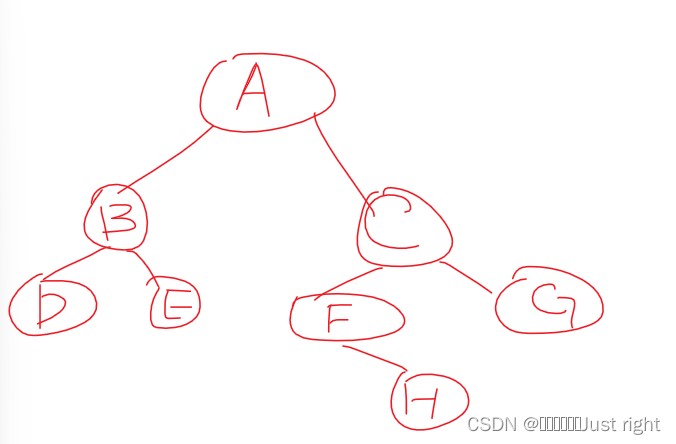
前序:ABDECFHG
例题2 已知先序,中序,求后序并构造二叉树
已知二叉树的前序遍历序列为ABCDEFG
中序遍历序列为CBEDFGA,构造二叉树,写出后序遍历序列
一句话:前序找根节点,中序区分左右
- 从前序中可以知道根节点是A,且左子树得根节点为B,从中序中可以知道CBEDFG是左子树
- 从先序(BCDEFG)可以知道B的右孩子是D,且B的左孩子是C,从中序(EDFG)中可以知道D的左孩子是E,从中序(EDFG)可以知道D的右子树中有FG,从前序遍历DEFG可以知道D的右孩子是F,从中序遍历(FG)中可以得到F的右孩子是G
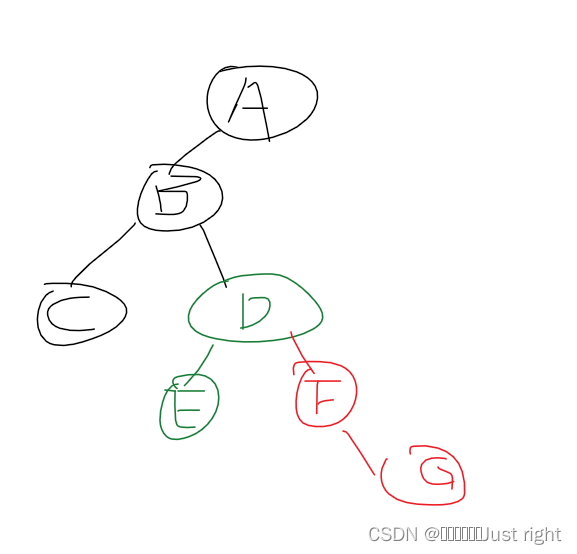
后序:CEGFDBA
例题3 已知先序,中序,求后序
先序遍历序列为A,B,C,D,E,F 中序遍历序列为C,B,A,E,D,F 求后序遍历序列
先序找根节点,中序确定左右
- 根节点为A,左子树的根节点为B,右子树的根节点为D
- 由中序遍历可得,B的左孩子是C,D的左孩子是E,D的右孩子是F
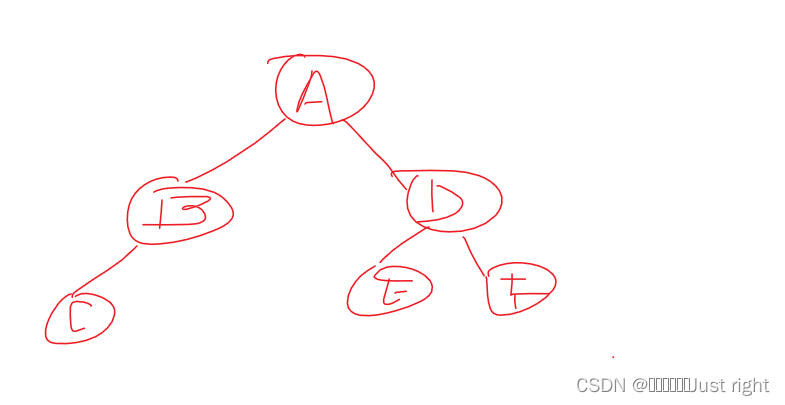
后序遍历:CBEFDA
哈夫曼树的构造
我只说我个人的理解,在给定的数据序列中找最小的两个,小的在左边,大的在右边,组成二叉树,在数据序列中删除此次找到的两个数,并加入此次最小两个数的权值之和
重复第一步,直至数据序列只有一个,最后添加0和1,左0右1
看题目把
例题1
在给出的数据序列{3,4,6,8,10,12,18}为叶子结点的权值所构造的哈夫曼树,并计算该树的带权路径长度
构造哈夫曼树
第一步
从3,4,6,8,10,12,18中找两个最小的数,小的在左边,大的在右边,组成二叉树,在数据序列中删除此次找到的两个数,并加入此次最小两个数的权值之和。
找到的是3和4,在给定的数据序列中删除3和4,加入7到末尾,数据序列更新为6,8,10,12,18,7
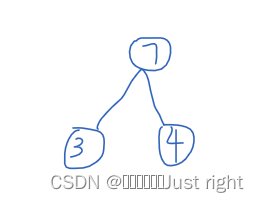
接下来重复
这次找到的是6和7,在给定的数据序列中删除6和7,在末尾添加13,数据序列更新为8,10,12,18,13
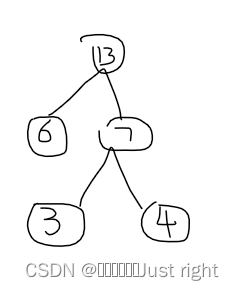
这次找到的是8和10,在给定的数据序列中删除8和10,在末尾添加18,数据序列更新为12,18,13,18
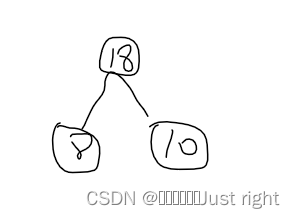
这次找到的是12和13,删除12和13,在末尾添加25,数据序列更新为18,18,25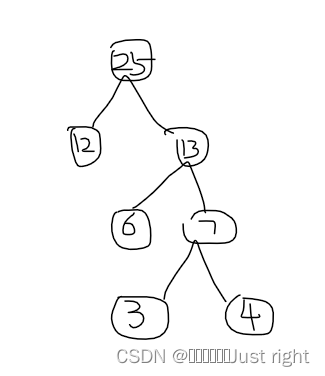 这次找到的是18和18,两个数相同的时候,放左边还是放右边无所谓,将18,18在数据序列中删除,在末尾添加36
这次找到的是18和18,两个数相同的时候,放左边还是放右边无所谓,将18,18在数据序列中删除,在末尾添加36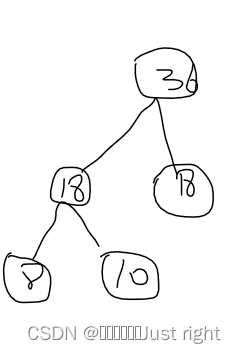 这次找到的是25和36,将25和36从数据序列中删除,将61插入到末尾,至此数据序列只剩下了一个,标0和1,左0右1,完成
这次找到的是25和36,将25和36从数据序列中删除,将61插入到末尾,至此数据序列只剩下了一个,标0和1,左0右1,完成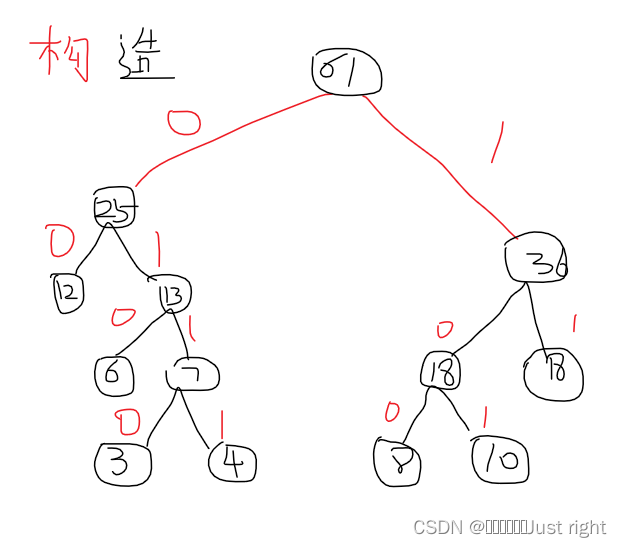
计算带权路径长度
路径就是从根结点出发,到目的结点(都是叶子结点)有几条线
上面的图中
从根节点出发到3,有4条线,长度为4
从根节点出发到4,有4条线,长度为4
从根节点出发到6,有3条线,长度为3
从根节点出发到8,有3条线,长度为3
从根节点出发到10,有3条线,长度为3
从根节点出发到12,有2条线,长度为2
从根节点出发到18,有2条线,长度为2,
相加求和
WPL=各个结点的权值乘以长度的总和
WPL=34+44+63+83+103+122+18*2=160







![[附源码]计算机毕业设计springboot电商小程序](https://img-blog.csdnimg.cn/f64b56c793b84f528a8837f773a7f4e4.png)