( “树” 之 BFS) 637. 二叉树的层平均值 —

( “树” 之 BFS) 637. 二叉树的层平均值 ——【Leetcode每日一题】

news2025/11/3 21:51:34

637. 二叉树的层平均值

给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 $10^{-5}$ 以内的答案可以被接受。

示例 1：

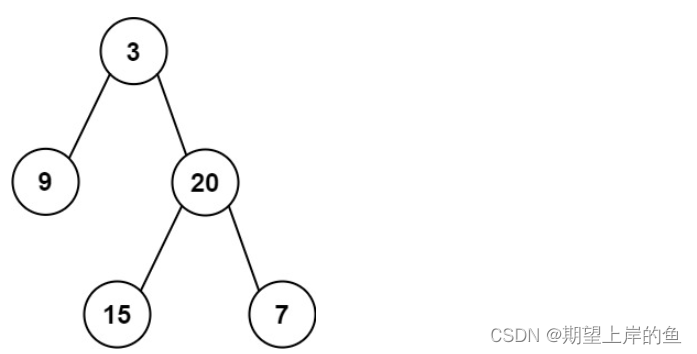
在这里插入图片描述

输入：root = [3,9,20,null,null,15,7]
输出：[3.00000,14.50000,11.00000]
解释：第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。

示例 2:

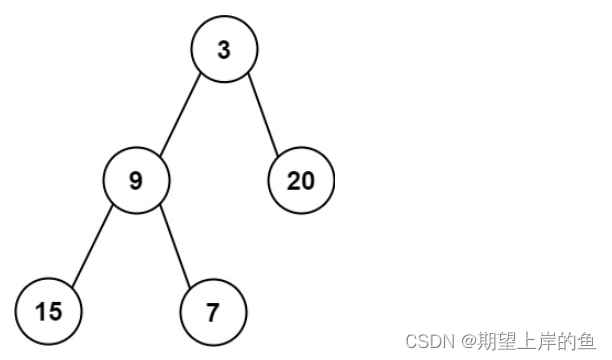
在这里插入图片描述

输入：root = [3,9,20,15,7]
输出：[3.00000,14.50000,11.00000]

提示：

树中节点数量在 $1, 10^4]$ 范围内
$2^{31} <= Node.val <= 2^{31} - 1$

思路：BFS

使用 BFS 进行层次遍历。

不需要使用两个队列来分别存储当前层的节点和下一层的节点

因为在开始遍历一层的节点时，当前队列中的节点数就是当前层的节点数，只要控制遍历这么多节点数，就能保证这次遍历的都是当前层的节点。

代码：(Java、C++)

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Double> averageOfLevels(TreeNode root) {
        List<Double> ans = new ArrayList<>();
        Queue<TreeNode> que = new LinkedList<>();
        que.add(root);
        while(!que.isEmpty()){
            int len = que.size();
            double sum = 0;
            for(int i = 0; i < len; i++){
                root = que.poll();
                sum += root.val;
                if(root.left != null) que.add(root.left);
                if(root.right != null) que.add(root.right);
            }
            ans.add(sum / len);
        }
        return ans;
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<double> averageOfLevels(TreeNode* root) {
        vector<double> ans;
        queue<TreeNode*> que;
        que.push(root);
        while(!que.empty()){
            int len = que.size();
            double sum = 0;
            for(int i = 0; i < len; i++){
                root = que.front();
                que.pop();//pop返回的是void
                sum += root->val;
                if(root->left != NULL) que.push(root->left);
                if(root->right != NULL) que.push(root->right);
            }
            ans.push_back(sum / len);
        }
        return ans;
    }
};

运行结果：

在这里插入图片描述

复杂度分析：

时间复杂度： $O (n)$ ，其中 n 是二叉树中的节点个数。广度优先搜索需要对每个节点访问一次，时间复杂度是 $O (n)$ 。需要对二叉树的每一层计算平均值，时间复杂度是 $O (h)$ ，其中 h 是二叉树的高度，任何情况下都满足 $h \leq n$ 。因此总时间复杂度是 $O (n)$ 。
空间复杂度： $O (n)$ ，其中 n 是二叉树中的节点个数。空间复杂度取决于队列开销，队列中的节点个数不会超过 n。