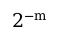Pytorch中很多函数都采用的是函数式索引的思路，而且使用函数式索引对代码可读性会有很大提升。

张量的符号索引

张量也是有序序列，我们可以根据每个元素在系统内的顺序位置，来找出特定的元素，也就是索引。

一维张量的索引

一维张量索引与Python中的索引一样是是从左到右，从0开始的，遵循格式为[start: end: step]。

>>> data = torch.arange(1, 11)
>>> print(data)
tensor([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10])
>>> data[0]
tensor(1)

张量索引出的结果是零维张量，而不是单独的数。要转化成数，需要使用item()方法：

>>> data[0].item()
1

批注：构成一维张量的是零维张量，而不是单独的数。

>>> data[3:9:2] # 隔2个数取一个，左闭右开
tensor([4, 6, 8])

在Python中，step可以为负数，例如:

>>> num_list = [1, 2, 3]
>>> num_list[::-1]
[3, 2, 1]

但在张量中，step必须大于0，否则就会报错。

>>> num_tensor = torch.arange(1, 11)
>>> num_tensor[::-1]
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: step must be greater than zero

二维张量的索引

二维张量的索引逻辑和一维张量的索引逻辑相同，二维张量可以视为两个一维张量组合而成。

>>> data2 = torch.arange(1, 21).reshape(4, 5)
>>> data2
tensor([[ 1,  2,  3,  4,  5],
        [ 6,  7,  8,  9, 10],
        [11, 12, 13, 14, 15],
        [16, 17, 18, 19, 20]])
>>> data2[0, 1], data2[0][1]  # 这两种索引方式都可以
(tensor(2), tensor(2))

但是data2[::2, ::2]与data2[::2][ ::2]的索引结果就不同：

>>> data2[::2, ::2]
tensor([[ 1,  3,  5],
        [11, 13, 15]])
>>> data2[::2][::2]
tensor([[1, 2, 3, 4, 5]])

解释：

• t2[::2, ::2]二维索引使用逗号隔开时，可以理解为全局索引，取第一行和第三行的第一列和第三列的元素。
• t2[::2][::2]二维索引在两个中括号中时，可以理解为先取了第一行和第三行，构成一个新的二维张量，然后在此基础上又间隔2并对所有张量进行索引。

>>> d = data2[::2]
>>> d
tensor([[ 1,  2,  3,  4,  5],
        [11, 12, 13, 14, 15]])
>>> d[::2]
tensor([[1, 2, 3, 4, 5]])

三维张量的索引

设三维张量的shape是x、y、z，则可理解为它是由x个二维张量构成，每个二维张量由y个一维张量构成，每个一维张量由z个元素构成。

>>> data3 = torch.arange(1, 25).reshape(2, 3, 4)
>>> data3
tensor([[[ 1,  2,  3,  4],
         [ 5,  6,  7,  8],
         [ 9, 10, 11, 12]],

        [[13, 14, 15, 16],
         [17, 18, 19, 20],
         [21, 22, 23, 24]]])
>>> data3[1, 1, 1]
tensor(18)
>>> data3[1, ::2, ::2]
tensor([[13, 15],
        [21, 23]])

高维张量的思路与低维一样，就是围绕张量的“形状”进行索引。

张量的函数索引

除了常⽤的索引选择数据之外，PyTorch还提供了⼀些⾼级的选择函数：

• index_select(input, dim, index)：在指定维度dim上选取，⽐如选取某些⾏、某些列
• masked_select(input, mask)：例⼦如上，a[a>0]，使⽤ByteTensor进⾏选取
• non_zero(input)：⾮0元素的下标
• gather(input, dim, index)：根据index，在dim维度上选取数据，输出的size与index⼀样

index_select()

index_select(dim, index)表示在张量的哪个维度进行索引，索引的位置是多少。

torch.index_select()函数返回的是沿着输入张量的指定维度的指定索引号进行索引的张量子集。

torch.index_select(input, dim, index, out=None)

其函数参数有：

• input(Tensor) - 需要进行索引操作的输入张量；
• dim(int) - 需要对输入张量进行索引的维度；
• index(LongTensor) - 包含索引号的 1D 张量；

index_select函数指定index来对张量进行索引，index的类型必须为Tensor

由于 index_select 函数只能针对输入张量的其中一个维度的一个或者多个索引号进行索引，因此可以通过 PyTorch 中的高级索引来实现。下面列举三个例子来说明这个函数的用法：

1. 获取1D张量的第1个维度且索引号为2和3的张量子集

>>> data = torch.arange(9)
>>> sub_data1 = torch.index_select(data, dim=0, index=torch.tensor([2, 3]))
>>> sub_data2 = data[[2, 3]]
>>> data
tensor([0, 1, 2, 3, 4, 5, 6, 7, 8])
>>> sub_data1
tensor([2, 3])
>>> sub_data2
tensor([2, 3])

2. 获取2D张量的第2个维度且索引号为0和1的张量子集(第一列和第二列)

>>> data2 = torch.arange(9).view(3, 3)
>>> sub_data1 = torch.index_select(data2, dim=1, index=torch.tensor([0, 1]))
>>> sub_data2 = data2[:, [0, 1]]
>>> data2
tensor([[0, 1, 2],
        [3, 4, 5],
        [6, 7, 8]])
>>> sub_data1
tensor([[0, 1],
        [3, 4],
        [6, 7]])
>>> sub_data2
tensor([[0, 1],
        [3, 4],
        [6, 7]])

3. 获取3D张量的第1个维度且索引号为0的张量子集

>>> data3 = torch.arange(18).view(2, 3, 3)
>>> sub_data1 = torch.index_select(data3, dim=0, index=torch.tensor([0]))
>>> sub_data2 = data3[0]
>>> print(data3)
tensor([[[ 0,  1,  2],
         [ 3,  4,  5],
         [ 6,  7,  8]],

        [[ 9, 10, 11],
         [12, 13, 14],
         [15, 16, 17]]])
>>> print(sub_data1)
tensor([[[0, 1, 2],
         [3, 4, 5],
         [6, 7, 8]]])
>>> print(sub_data2)
tensor([[0, 1, 2],
        [3, 4, 5],
        [6, 7, 8]])

index_select 函数虽然简单，但是有几点需要注意：

• index 参数必须是1D长整型张量 (1D-LongTensor)；
• 使用 index_select 函数输出的张量维度和原始的输入张量维度相同。（即是说，原来是三维的张量，就会输出三维的张量）

>>> data_rand3 = torch.rand(3, 4)
>>> sub_data1 = torch.index_select(data_rand3, dim=0, index=torch.tensor([0]))
>>> sub_data2 = data_rand3[[0]]
>>> sub_data3 = data_rand3[0]
>>> print(sub_data1)
tensor([[0.1926, 0.6743, 0.9063, 0.0857]])
>>> print(sub_data2)
tensor([[0.1926, 0.6743, 0.9063, 0.0857]])
>>> print(sub_data3)
tensor([0.1926, 0.6743, 0.9063, 0.0857])
>>> print(sub_data1.size(), sub_data2.size(), sub_data3.size())
torch.Size([1, 4]) torch.Size([1, 4]) torch.Size([4])

上面的代码示例可以说明，三种方式索引出来的张量子集中的元素是一样的，不同的是索引出来的张量子集的形状。所以，前文才说 index_select 函数对输入张量进行索引可以使用高级索引实现。

masked_select()

masked_select()函数返回一个根据布尔掩码 (boolean mask) 索引输入张量的 1D 张量。其用法如下：

torch.masked_select(input, mask, out=None) → Tensor

具体地：

• input (Tensor) ： 输入张量
• mask (ByteTensor) ： 掩码张量，包含了二元索引值
• out (Tensor, optional) ： 目标张量

>>> data = torch.randn(5, 4)
>>> mask_index = data.ge(0)  # 筛选大于0的结果
>>> res = torch.masked_select(data, mask_index)
>>> print(data)
tensor([[ 2.5874, -1.5814, -0.6473, -0.1795],
        [-0.4612,  0.2462,  0.5025,  0.9862],
        [ 1.2485,  0.6655,  1.5536,  0.7446],
        [-1.2433,  1.8842, -0.6330, -0.8245],
        [-0.5634, -1.1724,  1.3369,  0.5930]])
>>> print(res)
tensor([2.5874, 0.2462, 0.5025, 0.9862, 1.2485, 0.6655, 1.5536, 0.7446, 1.8842,
        1.3369, 0.5930])

masked_select 函数最关键的参数就是布尔掩码 mask参数。其通过布尔张量mask的True或者False来决定输入张量对应位置的元素是否保留，最后返回一维张量。

很明显，这种操作是一一对应的关系（True就保留，False就舍去），这就需要mask和input的形状相同。

• 两者的形状可以完全相同，也即是input.shape = mask.shape；
• 广播机制，两者的形状可以不完全相同，但是必须要能够通过 PyTorch 中的广播机制广播成相同形状的张量。

广播机制 (Broadcast) 是在科学运算中经常使用的小技巧，它是一种轻量级的张量复制手段，只在逻辑层面扩展和复制张量，并不进行实际的存储复制操作，从而大大的减少了计算代价。但并不是所有形状不一致的张量都能进行广播，需要满足一定的规则。比如对于两个张量来说：

• 如果两个张量的维度不同，则将维度小的张量进行扩展，直到两个张量的维度一样；
• 如果两个张量在对应维度上的长度相同或者其中一个张量的长度为 1，那么就说这两个张量在该维度上是相容的；
• 如果两个张量在所有维度上都是相容的，表示这两个张量能够进行广播，否则会出错；
• 在任何一个维度上，如果一个张量的长度为 1，另一个张量的长度大于 1，那么在该维度上，就好像是对第一个张量进行了复制；

masked_select 函数中的广播机制比较简单，只需要保证输入张量不变，对布尔张量进行广播，而广播后的形状和输入张量的形状一致就可以了。

>>> data = torch.arange(8).view(2, 4)
>>> mask2 = torch.tensor([True, True, False, True])  # 能广播
>>> print(data)
tensor([[0, 1, 2, 3],
        [4, 5, 6, 7]])
>>> print(torch.masked_select(data, mask2))
tensor([0, 1, 3, 4, 5, 7])

需要注意两点：

• 使用 masked_select 函数返回的结果都是 1D 张量，张量中的元素就是被筛选出来的元素值；
• 传入 input 参数中的输入张量和传入 mask 参数中的布尔张量形状可以不一致，但是布尔张量必须要能够通过广播机制扩展成和输入张量相同的形状；

问题来了，注意看下面的代码示例：

>>> data = torch.randn(3, 4)
>>> mask = data.ge(0)
>>> print(data[mask])
>>> print(torch.masked_select(data, mask))

tensor([[False,  True,  True, False],
        [ True, False,  True,  True],
        [ True, False,  True,  True]])
tensor([0.5393, 0.2735, 0.9606, 0.0107, 0.0654, 0.8304, 0.8467, 0.0034])
tensor([0.5393, 0.2735, 0.9606, 0.0107, 0.0654, 0.8304, 0.8467, 0.0034])

可以发现，masked_select函数其实没太大必要，直接通过data[mask]就可以达到效果了。那这个函数存在的意义在哪呢？这个问题留待后续…

non_zero()

non_zero()函数用于输出数组的非零值的索引，即用来定位数组中非零的元素。其用法如下：

torch.nonzero(input, *, out=None, as_tuple=False) → LongTensor or tuple of LongTensors

参数为：

• input：输入的数组
• as_tuple：函数返回方式，默认为False

如果设为False，则返回一个二维张量，其中每一行都是非零值的索引，如果输入的数组有$n$维，则输出的张量维度大小为$z\times n$，其中$z$为input非零元素的总数。

>>> a = torch.randn(3, 5)
>>> a = torch.where(x < 0, x, 0)  # 将非负元素置0
>>> print(a)
tensor([[ 0.0000, -1.0246, -0.2621,  0.0000],
        [ 0.0000, -0.7053, -0.8949, -0.3949],
        [ 0.0000, -0.1732, -0.4669,  0.0000],
        [ 0.0000, -1.0170, -1.1945,  0.0000],
        [ 0.0000,  0.0000,  0.0000, -0.4522]])
>>> print(torch.nonzero(a))
tensor([[0, 1],
        [0, 2],
        [1, 1],
        [1, 2],
        [1, 3],
        [2, 1],
        [2, 2],
        [3, 1],
        [3, 2],
        [4, 3]])

这里nonzero函数输出的结果，就是非零元素的索引。比如第一行[0, 1]代表这源Tensor里面第0行第1列的元素非零。

如果as_tuple设为True，则返回一个由一维张量组成的元组。看下面的输出：

>>> a = torch.randn(3, 5)
>>> a = torch.where(x < 0, x, 0)  # 将非负元素置0
>>> print(a)
tensor([[ 0.0000, -1.0246, -0.2621,  0.0000],
        [ 0.0000, -0.7053, -0.8949, -0.3949],
        [ 0.0000, -0.1732, -0.4669,  0.0000],
        [ 0.0000, -1.0170, -1.1945,  0.0000],
        [ 0.0000,  0.0000,  0.0000, -0.4522]])
>>> print(torch.nonzero(a, as_tuple=True))
(tensor([0, 0, 1, 1, 1, 2, 2, 3, 3, 4]), tensor([1, 2, 1, 2, 3, 1, 2, 1, 2, 3]))

如果输入数组为$n$维，则有$n$个一维张量，每个一维张量对应非零元素特定维度的索引（第一个张量数组储存的是所有非零元素第一维度的索引），并且每个张量里面有$z$个数，其中$z$为输入数组非零元素的个数。

这个函数除了找出非零元素外，还可用于特定元素定位，比如：

>>> a = torch.arange(12).view(3, 4)
>>> print(a)
tensor([[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]])
>>> torch.nonzero(a == 6)  # 输入元素为6的位置
tensor([[1, 2]])

gather()

gather()函数作用：沿给定轴dim，将输入索引张量index指定位置的值进行聚合。（沿着给定的维度dim收集值）

其用法为：

torch.gather(input, dim, index, out=None)

参数解释为：

• input(Tensor)：源张量
• dim(int)：索引的轴
• index(LongTensor)：聚合元素的下标
• out：目标张量

注意：index的维度要和input中dim所指的维度相同

torch.gather()常用索引多分类中标签所对应的概率。

例子1：按照dim = 0, 取一个二维张量对角线上的数值

>>> a = torch.tensor([[2, 3, 5], [4, 9, 7]])
>>> index = torch.LongTensor([[0, 1, 0]])
>>> b = torch.gather(a, dim=0, index=index)
>>> print(a)
tensor([[2, 3, 5],
        [4, 9, 7]])
>>> print(b)
tensor([[2, 9, 5]])

可以看到dim=0，即行方向的维度和index的维度是匹配的，就是说a和index由行方向从左往右看，有2列，即有2个样本，行方向是匹配的。另外，函数输出的tensor和index大小相同。

上面代码的操作逻辑可以用下图来表示。

具体地：在a中，由行从左往右看，有两个样本，索引分别为0和1；每个样本有两个特征，每个特征中从上往下索引分别为0和1；依据index中的索引值，取第0样本的第0个特征2，再取第1个样本的第1个特征7。

例子2：按照dim = 1, 取一个二维张量的对角线上的数值

>>> a = torch.tensor([[2, 3], [4, 9], [6, 10]])
>>> index = torch.LongTensor([[0], [1], [0]])
>>> b = torch.gather(a, dim=1, index=index)
>>> print(a)
tensor([[ 2,  3],
        [ 4,  9],
        [ 6, 10]])
>>> print(b)
tensor([[2],
        [9],
        [6]])

可以看到dim=1，即列方向的维度和index的维度是匹配的，就是说a和index由列方向从上往下看，有3行，即有3个样本，列方向是匹配的。另外，函数输出的tensor和index大小相同。

上面代码的操作逻辑可以用下图来表示。

具体地：在a中，由列从上往下看，有三个样本，索引分别为0、1和0；每个样本有两个特征，每个特征中从左往右索引分别为0和1；依据index中的索引值，取第0样本的第0个特征2，取第1个样本的第1个特征7，再取第2个样本的第1个特征6。

例子3：模拟多分类问题中的概率取值（跟上面的两个例子一样）

>>> a = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
>>> index = torch.LongTensor([[0], [2]])
>>> a
tensor([[0.1000, 0.3000, 0.6000],
        [0.3000, 0.2000, 0.5000]])
>>> a.gather(dim=1, index=index)
tensor([[0.1000],
        [0.5000]])

---

总结：根据维度按行或者列根据索引取值

• dim=0：在列上按索引取值
• dim=1：在行上按索引取值