定点数的二进制表示形式

什么是定点数

在嵌入式系统中，为了降低运算复杂度，通常还会使用定点数格式。

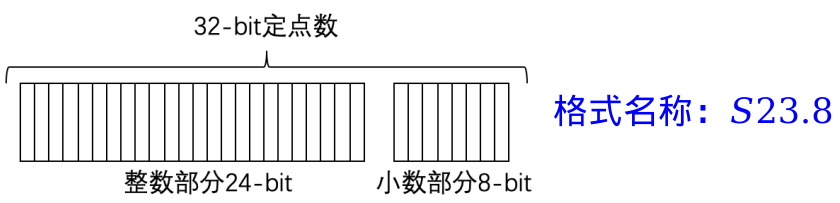
图中32位定点数的存储占用了32位的空间，其中24位为整数部分，8位为小数部分，定点数格式对应的数值为

从存储空间看，32位定点数的存储空间和单精度浮点数相同，但定点数的加减乘除运算可以直接使用整数运算电路实现，硬件复杂度远小于浮点数电路，因此在嵌入式系统和DSP芯片中得到广泛应用。

表示格式

Sn·m

其中，S表示有符号（Signed），n为 定点数的总位数，m 为小数的位数

考虑到要用二进制的补码形式表示负数，总的位数为 n + m + 1

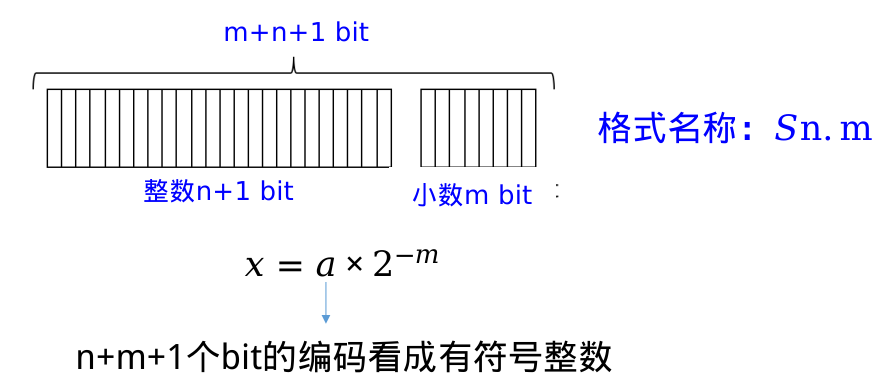
Example:

给定S2.13 格式的定点数二进制形式：

111 1000000000001

总共16位，看成有符号整数就是 -4095，计算时要先减1再取反，即可得100 011111111111，对应的数值就是：

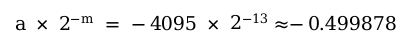
数值范围与分辨率

由于传统的CPU 对应数据访问的单位是 8位、16位、32位，因此定点数往往也使用这几种位宽。

对于 Sn·m 定点数，能够表达的最大数为

最小数为

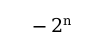
分辨率为

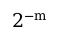
常用的8位和16位定点数格式信息

<![if supportMisalignedColumns]> <![endif]>

总位宽	格式名称	小数位数	最小值	最大值	分辨率
16-bit	S0.15	15	-1	1	3E-05
	S1.14	14	-2	1.9999	6E-05
	S2.13	13	-4	3.9999	0.0001
	S3.12	12	-8	7.9998	0.0002
	S4.11	11	-16	16	0.0005
	S5.10	10	-32	31.999	0.001
	S6.9	9	-64	63.998	0.002
	S7.8	8	-128	128	0.0039
	S8.7	7	-256	255.99	0.0078
	S9.6	6	-512	511.98	0.0156
	S10.5	5	-1024	1024	0.0313
	S11.4	4	-2048	2047.9	0.0625
	S12.3	3	-4096	4095.9	0.125
	S13.2	2	-8192	8191.8	0.25
	S14.1	1	-16384	16384	0.5
	S15.0	0	-32768	32767	1
8-bit	S0.7	7	-1	0.9922	0.0078
	S1.6	6	-2	1.9844	0.0156
	S2.5	5	-4	3.9688	0.0313
	S3.4	4	-8	7.9375	0.0625
	S4.3	3	-16	15.875	0.125
	S5.2	2	-32	31.75	0.25
	S6.1	1	-64	63.5	0.5
	S7.0	0	-128	127	1

给定一个浮点数，将它定点化后，对应值和原始数值会有误差，这是定点数表示小数点位数长度有限造成的，最大误差不超过上表的分辨率。

转换

python 转换定点数

def double_to_fxp(v,n=0,m=15):
        i=round(v*2.**m) // 转为整数
        i=min( 2**(n+m)-1,i) # 与 2^15 - 1 比较，判断上限
        i=max(-2**(n+m)  ,i) # 与 - 2^15 比较，判断下限
        return i/2.**m # 转为小数
    
print(math.pi)
v10_5_pi =double_to_fxp(math.pi ,10 ,5)
print(v10_5_pi)
print(v10_5_pi -math.pi)

结果：

3.141592653589793
3.15625
0.014657346410206884

C 双精度浮点数转换为8位和16位定点数

#define FLOAT(v) ((float)(v))

#define INT32(v) ((signed long)(v))
#define UINT32(v) ((unsigned long)(v))
#define INT16(v) ((signed short)(v))
#define UINT16(v) ((unsigned short)(v))
#define INT8(v) ((signed char)(v))

#define ROUND(v) ((v) > 0 ? int32_t((v) + 0.5) : int32_t((v) - 0.5))

signed short to_fxp16(double v, int m) {
  v *= FLOAT(1L << m); // m位小数移到整数部分
  signed long vi = ROUND(v); // 取整后整好保留 m 位小数
  if (vi > 332767) {
    vi = 32767;
  }
  if (vi < -32768) {
    vi = -32768;
  }
  return INT16(vi); // 转换为16整数
}

signed short to_fxp8(double v, int m) {
  v *= FLOAT(1L << m);
  signed long vi = ROUND(v);
  if (vi > 127) {
    vi = 127;
  }
  if (vi < -128) {
    vi = -128;c++
  }
  return INT8(vi);
}

整体思想就是，如果要转为 m 为定点数，则先将 double 扩大 m 倍，即将 m 位的小数转移到整数部分，然后取整，进行小数位数截断

C 将定点数转回浮点数

只要将编码当做整数并除以小数位宽对应比例因子即可

#define to_double(v,m) ((double)(v) / ((double)(1L << m)))

测试

int main() {
  char ch[16];
  double v = M_PI;
  
  short sv = to_fxp16(v, 5);
  std::cout << "sv 二进制： " << std::bitset<16>(sv) << std::endl;
  double svd = to_double(sv, 5);
  printf("1L << m: %ld\n", 1L << 5);
  printf("v: %f\n", v);
  printf("sv: %d\n", sv);
  printf("svd: %f\n", svd);
  printf("diff: %f\n", v-svd);
  return 0;
}

结果：

v: 3.141593
v 二进制：  0000000000000011
sv: 101
sv 二进制： 0000000001100101v
svd: 3.156250
diff: -0.014657