单值二叉树(力扣)
---------------------------------------------------哆啦A梦的任意门-------------------------------------------------------
我们来看一下题目的具体要求:

既然我们都学了二叉树了,我们就应该学会如何去递归。
分析一下:
我们如果去用遍历的思路去做,肯定是可以做出来的,遍历嘛,先将第一次出现的数给存起来作为一个key,那么遍历整个二叉树,如果出现了一个不同于这个key的数值,那么我们就说这个二叉树不是单值二叉树,如果到最后访问完整个二叉树都没有出现一个不同于这个key的值,那么我们就可以说这个二叉树是一个单值二叉树。
但是看了一下这个思路,一个个遍历是不是显得十分的龊啊?
那么我们就要用二叉树独特的特点,根和它的左子树和右子树进行对比,以此来递归。
我们是不是就突然之间就想出做法了呢?
那么思路如下:
用根的值和左子树和右子树的值进行对比。如果出现一次不相同就可以返回false了。
bool isUnivalTree(struct TreeNode* root){
if(root == NULL)
{
return true;
}
if(root->left != NULL && root->left->val != root->val)
{
return false;
}
if(root->right != NULL && root->right->val != root->val)
{
return false;
}
return isUnivalTree(root->left) && isUnivalTree(root->right);
}只要遇到底层的NULL,我们直接返回true,因为只要出现左子树或右子树返回了一个false,整个二叉树就不是单值二叉树了。所以用&&运算符。
二叉树最大深度(力扣)
---------------------------------------------------哆啦A梦的任意门-------------------------------------------------------
来看一下题目要求:
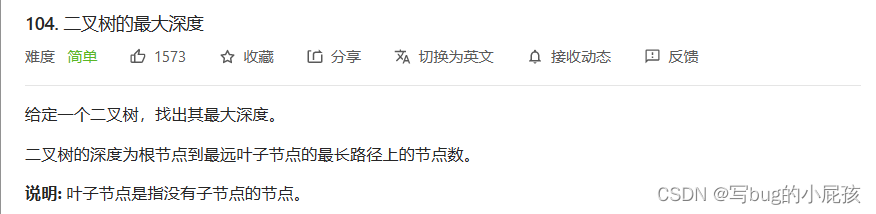
二叉树是由根-左子树-右子树构成的,所以如果要知道二叉树的最大深度,我们就去找到左子树和右子树当中最深的那棵树的具体深度 + 1就是我们这棵树的最大深度了。
那么出现递归结束的条件也是很简单啊,就是我们访问的一个根,这个根如果是空的,我们就可以返回0,别问我为什么不返回1,空的为啥要返回1?
所以来看代码叭~
int maxDepth(struct TreeNode* root){
if(root == NULL)
{
return 0;
}
int left = maxDepth(root->left);
int right = maxDepth(root->right);
if(left < right)
{
return 1 + right;
}
return 1 + left;
}翻转二叉树(力扣)
---------------------------------------------------哆啦A梦的任意门-------------------------------------------------------
还是来看一下题目要求~
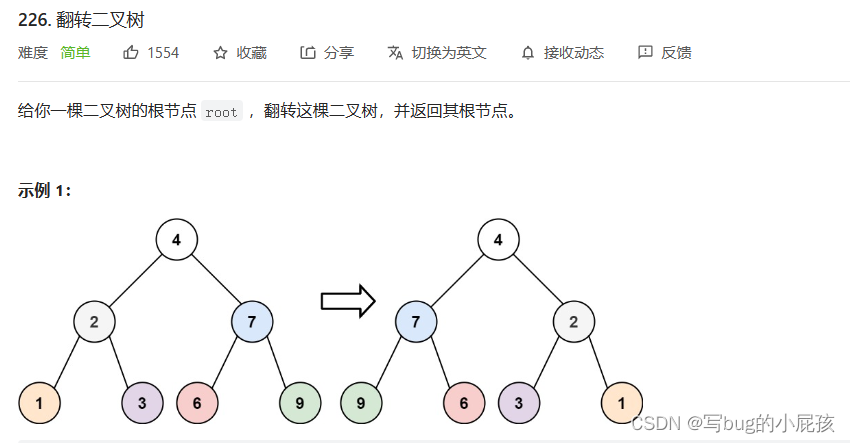
光看这个题目完全不懂它的意思,但是一看这个图就明白了。
我们就是需要让一个根的两个子树翻转过来,让一个根的左子树作为它的右子树,它的右子树作为它的左子树。
那么思路就很清晰了,我们的递归结束条件就是当遇到空的时候,我们就返回该结点。
直接来看代码叭~
void swap(struct TreeNode** x1,struct TreeNode** x2)
{
struct TreeNode* tmp = *x1;
*x1 = *x2;
*x2 = tmp;
}
struct TreeNode* invertTree(struct TreeNode* root){
if(root == NULL)
{
return root;
}
swap(&(root->left),&(root->right));
invertTree(root->left);
invertTree(root->right);
return root;
}如上,我们写了一个交换函数,但是和平时的交换函数好像不太一样啊,为什么这个指针是个二级指针。我们回到这个翻转二叉树的函数当中,我们发现传进去的是root->left和root->right,我们发现这传进去的是一个指针。我们需要改变一个指针,就需要传入一个指针的指针,也就是二级指针,所以,这就是为什么这个交换函数的两个形参是两个二级指针。
检查两颗树是否相同(力扣)
---------------------------------------------------哆啦A梦的任意门-------------------------------------------------------
看题目的要求:
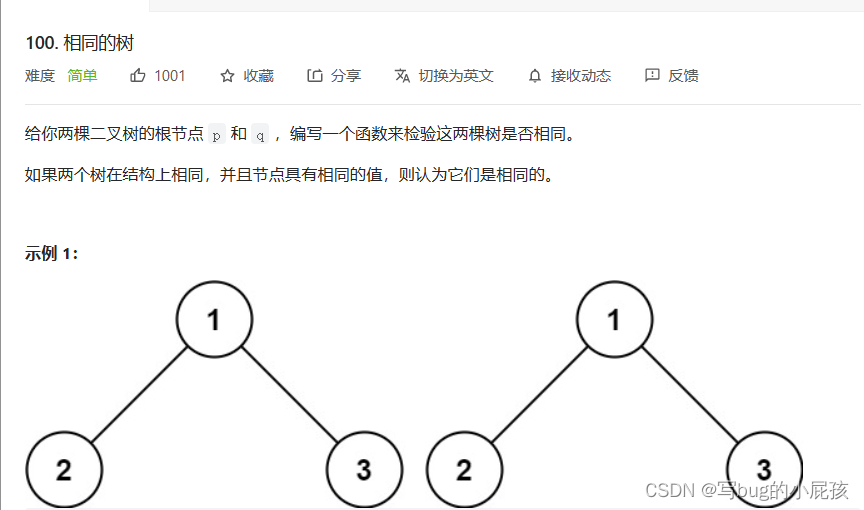
分析一下:
结果为false的几种可能:
1.对比某个结点时,我们发现这两个结点的值不是相等的,那么返回false
2.其中一棵二叉树先遇到了NULL,而另一棵树还没遇到NULL,那么返回false
如果对应的值相等,而且同时出现遇到了NULL,那么我们就返回true。
所以来看代码:
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
if(p == NULL && q == NULL)
{
return true;
}
//若p和q同时都为NULL,就早已return了
if(p == NULL || q == NULL)
{
return false;
}
if(p->val != q->val)
{
return false;
}
return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}对称二叉树(力扣)
---------------------------------------------------哆啦A梦的任意门-------------------------------------------------------
看题:
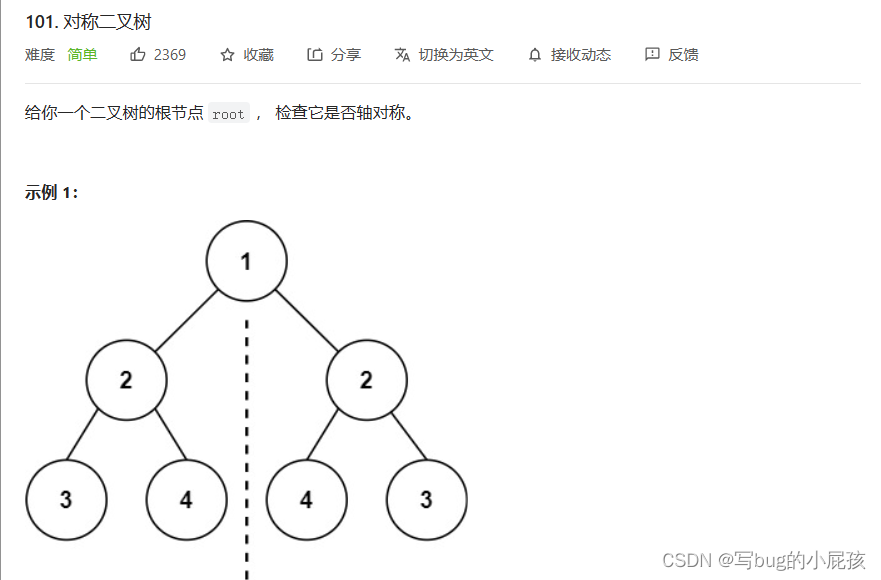
我们来观察一下,根只有一个,肯定是对称的啦,它的两个左右孩子都是相等的,也就是对称的。那么再看它的两个左右孩子的左右孩子,我们可以发现,如果要让这两个子树对称,那么就需要让这棵左子树的右子树等于右子树的左子树,左子树的左子树等于右子树的右子树。
思路:
判断一个树是否对称,首先要判断左右孩子是否对称相等,还需要判断左孩子的左子树是否和右孩子的右子树对称,左孩子的右子树是否和右孩子的左子树对称。
bool check(struct TreeNode* p,struct TreeNode* q)
{
if(p == NULL && q == NULL)
return true;
if(p == NULL || q == NULL)
return false;
return p->val == q->val && check(p->left,q->right) && check(p->right, q->left);
}
bool isSymmetric(struct TreeNode* root){
return check(root->left,root->right);
}如果同时为NULL,那么就返回true,如果出现其中一个出现了NULL,另一个没有出现NULL,那么直接返回false
另一颗树的子树(力扣)
---------------------------------------------------哆啦A梦的任意门-------------------------------------------------------
先来看一下题目的要求:
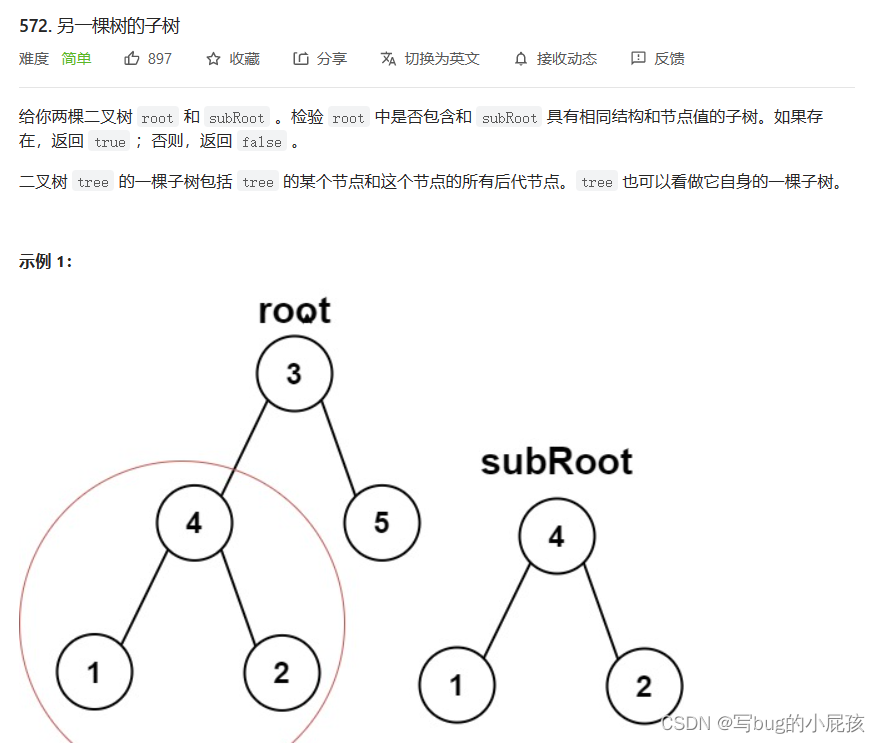
这个像不像上面的有一道题?那道比较两个树是否相等的题。
其实对比两个树是否相等的思路是一样的,只不过我们要找到是否这棵子树是否存在于另一棵树当中。
我们是不是先去root找到一个与subRoot的根节点一样的结点呢?
之后往下比较两棵树是否相等就好了?
那么我们还是从根出发,去它的左子树和右子树去寻找这一棵能和subRoot能完全吻合的子树。
如果在左子树找不着,那就去右子树找,如果都找不到,那么就只能返回一个false了
来看代码:
bool isSame(struct TreeNode* s, struct TreeNode* t)
{
if(!s && !t)
return true;
if(!s || !t)
return false;
if(s->val != t->val)
return false;
return isSame(s->left,t->left) && isSame(s->right,t->right);
}
bool isSubtree(struct TreeNode* s, struct TreeNode* t) {
if(!s)
return false;
if(isSame(s,t))
return true;
return isSubtree(s->left,t) || isSubtree(s->right,t);
}从这段代码,我们的思路还是比较清晰的。
我们从根出发,先看看这个根开始,能不能与这棵子树吻合,如果不吻合就继续往下走,结束的条件也就是我们遇到了NULL,说明这个根已经到了底下了,不可能再有结点了,直接返回来。