主要记录算法和数据结构学习笔记，新的一年更上一层楼！

• 满二叉树 节点数量为2^k-1
• 完全二叉树除了底层以外其他层全是满的，底层从左到右连续
• 二叉搜索树左小右大
• 平衡二叉搜索树左子树和右子树的高度之差的绝对值不超过1，平衡因子为-1,0,1。在c++中map、set底层平衡二叉搜索树
• 存储方式： 链式存储、顺序存储(左孩子2i+1，右孩子2i+2)
• 深度优先搜索（前、中、后序遍历）【从某顶点，依次从它各个未被访问的邻接点出发遍历，直到所有被访问】、广度优先搜索【从某顶点访问v后，依次访问v的各个未被访问的邻接点】
• 前序遍历中左右，中序遍历左中右，后序遍历左右中

一、递归遍历

1.题目：递归遍历：leetcode144 94 145

2.解题思路：

//前序遍历
var preorderTraversal = function(root) {
 let res=[];
 const dfs=function(root){
     if(root===null)return ;
     //先序遍历所以从父节点开始
     res.push(root.val);
     //递归左子树
     dfs(root.left);
     //递归右子树
     dfs(root.right);
 }
 //只使用一个参数 使用闭包进行存储结果
 dfs(root);
 return res;
};
//60ms
//41MB

//中序遍历
var inorderTraversal = function(root) {
    let res=[];
    const dfs=function(root){
        if(root===null){
            return ;
        }
        dfs(root.left);
        res.push(root.val);
        dfs(root.right);
    }
    dfs(root);
    return res;
};
//72ms
//41MB

//后序遍历
var postorderTraversal = function(root) {
    let res=[];
    const dfs=function(root){
        if(root===null){
            return ;
        }
        dfs(root.left);
        dfs(root.right);
        res.push(root.val);
    }
    dfs(root);
    return res;
};
//64ms
//41MB

二、迭代遍历

1.题目：迭代遍历

2.解题思路：

//前序遍历:

// 入栈 右 -> 左
// 出栈 中 -> 左 -> 右
var preorderTraversal = function(root, res = []) {
    if(!root) return res;
    const stack = [root];
    let cur = null;
    while(stack.length) {
        cur = stack.pop();
        res.push(cur.val);
        cur.right && stack.push(cur.right);
        cur.left && stack.push(cur.left);
    }
    return res;
};

中序遍历:

// 入栈 左 -> 右
// 出栈 左 -> 中 -> 右

var inorderTraversal = function(root, res = []) {
    const stack = [];
    let cur = root;
    while(stack.length || cur) {
        if(cur) {
            stack.push(cur);
            // 左
            cur = cur.left;
        } else {
            // --> 弹出 中
            cur = stack.pop();
            res.push(cur.val); 
            // 右
            cur = cur.right;
        }
    };
    return res;
};

后序遍历:

// 入栈 左 -> 右
// 出栈 中 -> 右 -> 左 结果翻转

var postorderTraversal = function(root, res = []) {
    if (!root) return res;
    const stack = [root];
    let cur = null;
    do {
        cur = stack.pop();
        res.push(cur.val);
        cur.left && stack.push(cur.left);
        cur.right && stack.push(cur.right);
    } while(stack.length);
    return res.reverse();
};

三、统一迭代法

1.题目：二叉树的统一迭代法

2.解题思路：

// 前序遍历：中左右
// 压栈顺序：右左中

var preorderTraversal = function(root, res = []) {
    const stack = [];
    if (root) stack.push(root);
    while(stack.length) {
        const node = stack.pop();
        if(!node) {
            res.push(stack.pop().val);
            continue;
        }
        if (node.right) stack.push(node.right); // 右
        if (node.left) stack.push(node.left); // 左
        stack.push(node); // 中
        stack.push(null);
    };
    return res;
};

//  中序遍历：左中右
//  压栈顺序：右中左
 
var inorderTraversal = function(root, res = []) {
    const stack = [];
    if (root) stack.push(root);
    while(stack.length) {
        const node = stack.pop();
        if(!node) {
            res.push(stack.pop().val);
            continue;
        }
        if (node.right) stack.push(node.right); // 右
        stack.push(node); // 中
        stack.push(null);
        if (node.left) stack.push(node.left); // 左
    };
    return res;
};

// 后续遍历：左右中
// 压栈顺序：中右左
 
var postorderTraversal = function(root, res = []) {
    const stack = [];
    if (root) stack.push(root);
    while(stack.length) {
        const node = stack.pop();
        if(!node) {
            res.push(stack.pop().val);
            continue;
        }
        stack.push(node); // 中
        stack.push(null);
        if (node.right) stack.push(node.right); // 右
        if (node.left) stack.push(node.left); // 左
    };
    return res;
};

四、层序遍历

1.题目：层序遍历

2.解题思路：

var levelOrder = function(root) {
    //二叉树的层序遍历
    let res = [], queue = [];
    queue.push(root);
    if(root === null) {
        return res;
    }
    while(queue.length !== 0) {
        // 记录当前层级节点数
        let length = queue.length;
        //存放每一层的节点
        let curLevel = [];
        for(let i = 0;i < length; i++) {
            let node = queue.shift();
            curLevel.push(node.val);
            // 存放当前层下一层的节点
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
        //把每一层的结果放到结果数组
        res.push(curLevel);
    }
    return res;
};  

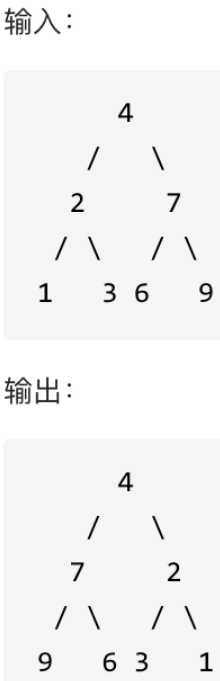
五、翻转二叉树

1.题目
翻转二叉树

2.**解题思路**：

```javascript
//递归的前序遍历
var invertTree = function(root) {
    // 终止条件
    if (!root) {
        return null;
    }
    // 交换左右节点
    const rightNode = root.right;
    root.right = invertTree(root.left);
    root.left = invertTree(rightNode);
    return root;
};

//迭代的前序遍历
var invertTree = function(root) {
    //我们先定义节点交换函数
    const invertNode = function(root, left, right) {
        let temp = left;
        left = right;
        right = temp;
        root.left = left;
        root.right = right;
    }
    //使用迭代方法的前序遍历 
    let stack = [];
    if(root === null) {
        return root;
    }
    stack.push(root);
    while(stack.length) {
        let node = stack.pop();
        if(node !== null) {
            //前序遍历顺序中左右  入栈顺序是前序遍历的倒序右左中
            node.right && stack.push(node.right);
            node.left && stack.push(node.left);
            stack.push(node);
            stack.push(null);
        } else {
            node = stack.pop();
            //节点处理逻辑
            invertNode(node, node.left, node.right);
        }
    }
    return root;
};

//层序遍历
var invertTree = function(root) {
    //我们先定义节点交换函数
    const invertNode = function(root, left, right) {
        let temp = left;
        left = right;
        right = temp;
        root.left = left;
        root.right = right;
    }
    //使用层序遍历
    let queue = [];
    if(root === null) {
        return root;
    } 
    queue.push(root);
    while(queue.length) {
        let length = queue.length;
        while(length--) {
            let node = queue.shift();
            //节点处理逻辑
            invertNode(node, node.left, node.right);
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
    }
    return root;
};

六、对称二叉树

1.题目：

2.解题思路：

//递归判断
var isSymmetric = function(root) {
    // 使用递归遍历左右子树 递归三部曲
    // 1. 确定递归的参数 root.left root.right和返回值true false 
    const compareNode = function(left, right) {
        // 2. 确定终止条件 空的情况
        if(left === null && right !== null || left !== null && right === null) {
            return false;
        } else if(left === null && right === null) {
            return true;
        } else if(left.val !== right.val) {
            return false;
        }
        // 3. 确定单层递归逻辑
        let outSide = compareNode(left.left, right.right);
        let inSide = compareNode(left.right, right.left);
        return outSide && inSide;
    }
    if(root === null) {
        return true;
    }
    return compareNode(root.left, root.right);
};

//队列实现迭代判断
var isSymmetric = function(root) {
  // 迭代方法判断是否是对称二叉树
  // 首先判断root是否为空
  if(root === null) {
      return true;
  }
  let queue = [];
  queue.push(root.left);
  queue.push(root.right);
  while(queue.length) {
      let leftNode = queue.shift();    //左节点
      let rightNode = queue.shift();   //右节点
      if(leftNode === null && rightNode === null) {
          continue;
      }
      if(leftNode === null || rightNode === null || leftNode.val !== rightNode.val) {
          return false;
      }
      queue.push(leftNode.left);     //左节点左孩子入队
      queue.push(rightNode.right);   //右节点右孩子入队
      queue.push(leftNode.right);    //左节点右孩子入队
      queue.push(rightNode.left);    //右节点左孩子入队
  }
  
  return true;
};

//栈实现迭代判断
var isSymmetric = function(root) {
  // 迭代方法判断是否是对称二叉树
  // 首先判断root是否为空
  if(root === null) {
      return true;
  }
  let stack = [];
  stack.push(root.left);
  stack.push(root.right);
  while(stack.length) {
      let rightNode = stack.pop();    //左节点
      let leftNode=stack.pop();       //右节点
      if(leftNode === null && rightNode === null) {
          continue;
      }
      if(leftNode === null || rightNode === null || leftNode.val !== rightNode.val) {
          return false;
      }
      stack.push(leftNode.left);      //左节点左孩子入队
      stack.push(rightNode.right);    //右节点右孩子入队
      stack.push(leftNode.right);     //左节点右孩子入队
      stack.push(rightNode.left);     //右节点左孩子入队
  }
  
  return true;
};

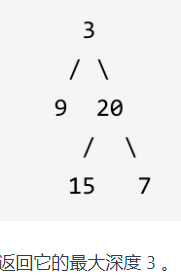
七、二叉树的最大深度

1.题目：
给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例

给定二叉树 [3,9,20,null,null,15,7]，

//递归遍历
var maxdepth = function(root) {
    //使用递归的方法 递归三部曲
    //1. 确定递归函数的参数和返回值
    const getdepth = function(node) {
    //2. 确定终止条件
        if(node === null) {
            return 0;
        }
    //3. 确定单层逻辑
        let leftdepth = getdepth(node.left);
        let rightdepth = getdepth(node.right);
        let depth = 1 + Math.max(leftdepth, rightdepth);
        return depth;
    }
    return getdepth(root);
};

//层级遍历
var maxDepth = function(root) {
    if(!root) return 0
    let count = 0
    const queue = [root]
    while(queue.length) {
        let size = queue.length
        /* 层数+1 */
        count++
        while(size--) {
            let node = queue.shift();
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
    }
    return count
};

八、二叉树的最小深度

1.题目：
给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明: 叶子节点是指没有子节点的节点。

示例

给定二叉树 [3,9,20,null,null,15,7]，
最小深度2

//递归遍历
/**
    * @param {TreeNode} root
    * @return {number}
    */
var minDepth1 = function(root) {
    if(!root) return 0;
    // 到叶子节点 返回 1
    if(!root.left && !root.right) return 1;
    // 只有右节点时 递归右节点
    if(!root.left) return 1 + minDepth(root.right);
    // 只有左节点时 递归左节点
    if(!root.right) return 1 + minDepth(root.left);
    return Math.min(minDepth(root.left), minDepth(root.right)) + 1;
};

//迭代遍历
/**
* @param {TreeNode} root
* @return {number}
*/
var minDepth = function(root) {
    if(!root) return 0;
    const queue = [root];
    let dep = 0;
    while(true) {
        let size = queue.length;
        dep++;
        while(size--){
            const node = queue.shift();
            // 到第一个叶子节点 返回 当前深度 
            if(!node.left && !node.right) return dep;
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
    }
};

九、完全二叉树的节点个数

1.题目：
给出一个完全二叉树，求出该树的节点个数。

示例

示例 1：

输入：root = [1,2,3,4,5,6]
输出：6
示例 2：

输入：root = []
输出：0
示例 3：

输入：root = [1]
输出：1

提示：
- 树中节点的数目范围是[0, 5 * 10^4]
- 0 <= Node.val <= 5 * 10^4
- 题目数据保证输入的树是 完全二叉树

//递归遍历
var countNodes = function(root) {
    //递归法计算二叉树节点数
    // 1. 确定递归函数参数
    const getNodeSum = function(node) {
    //2. 确定终止条件
        if(node === null) {
            return 0;
        }
    //3. 确定单层递归逻辑
        let leftNum = getNodeSum(node.left);
        let rightNum = getNodeSum(node.right);
        return leftNum + rightNum + 1;
    }
    return getNodeSum(root);
};

//迭代遍历
var countNodes = function(root) {
    //层序遍历
    let queue = [];
    if(root === null) {
        return 0;
    }
    queue.push(root);
    let nodeNums = 0;
    while(queue.length) {
        let length = queue.length;
        while(length--) {
            let node = queue.shift();
            nodeNums++;
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
    }
    return nodeNums;
};

//完全二叉树性质
var countNodes = function(root) {
    //利用完全二叉树的特点
    if(root === null) {
        return 0;
    }
    let left = root.left;
    let right = root.right;
    let leftDepth = 0, rightDepth = 0;
    while(left) {
        left = left.left;
        leftDepth++;
    }
    while(right) {
        right = right.right;
        rightDepth++;
    }
    if(leftDepth == rightDepth) {
        return Math.pow(2, leftDepth+1) - 1;
    }
    return countNodes(root.left) + countNodes(root.right) + 1;
};

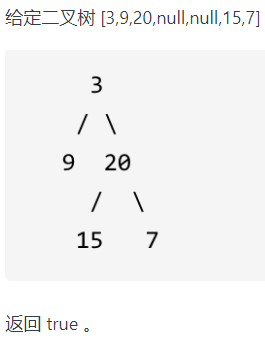
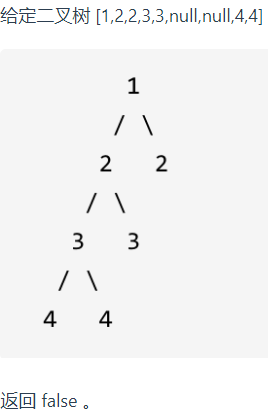
十、平衡二叉树

1.题目：
给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

示例
给定二叉树 [3,9,20,null,null,15,7]

//递归
var isBalanced = function(root) {
    //还是用递归三部曲 + 后序遍历 左右中 当前左子树右子树高度相差大于1就返回-1
    // 1. 确定递归函数参数以及返回值
    const getDepth = function(node) {
        // 2. 确定递归函数终止条件
        if(node === null) return 0;
        // 3. 确定单层递归逻辑
        let leftDepth = getDepth(node.left); //左子树高度
        // 当判定左子树不为平衡二叉树时,即可直接返回-1
        if(leftDepth === -1) return -1;
        let rightDepth = getDepth(node.right); //右子树高度
        // 当判定右子树不为平衡二叉树时,即可直接返回-1
        if(rightDepth === -1) return -1;
        if(Math.abs(leftDepth - rightDepth) > 1) {
            return -1;
        } else {
            return 1 + Math.max(leftDepth, rightDepth);
        }
    }
    return !(getDepth(root) === -1);
};

//迭代遍历
// 获取当前节点的高度
var getHeight = function (curNode) {
    let stack = [];
    if (curNode !== null) stack.push(curNode); // 压入当前元素
    let depth = 0, res = 0;
    while (stack.length) {
        let node = stack[stack.length - 1]; // 取出栈顶
        if (node !== null) {
            stack.pop();
            stack.push(node);   // 中
            stack.push(null);
            depth++;
            node.right && stack.push(node.right);   // 右
            node.left && stack.push(node.left);     // 左
        } else {
            stack.pop();
            node = stack[stack.length - 1];
            stack.pop();
            depth--;
        }
        res = res > depth ? res : depth;
    }
    return res;
}
var isBalanced = function (root) {
    if (root === null) return true;
    let stack = [root];
    while (stack.length) {
        let node = stack[stack.length - 1]; // 取出栈顶
        stack.pop();
        if (Math.abs(getHeight(node.left) - getHeight(node.right)) > 1) {
            return false;
        }
        node.right && stack.push(node.right);
        node.left && stack.push(node.left);
    }
    return true;
};

十一、二叉树的所有路径

1.题目：
给定一个二叉树，返回所有从根节点到叶子节点的路径。

说明: 叶子节点是指没有子节点的节点。

示例

//递归遍历
var binaryTreePaths = function(root) {
   //递归遍历+递归三部曲
   let res = [];
   //1. 确定递归函数 函数参数
   const getPath = function(node,curPath) {
    //2. 确定终止条件，到叶子节点就终止
       if(node.left === null && node.right === null) {
           curPath += node.val;
           res.push(curPath);
           return;
       }
       //3. 确定单层递归逻辑
       curPath += node.val + '->';
       node.left && getPath(node.left, curPath);
       node.right && getPath(node.right, curPath);
   }
   getPath(root, '');
   return res;
};

//迭代遍历
var binaryTreePaths = function(root) {
  if (!root) return [];
  const stack = [root], paths = [''], res = [];
  while (stack.length) {
    const node = stack.pop();
    let path = paths.pop();
    if (!node.left && !node.right) { // 到叶子节点终止, 添加路径到结果中
      res.push(path + node.val);
      continue;
    }
    path += node.val + '->';
    if (node.right) { // 右节点存在
      stack.push(node.right);
      paths.push(path);
    }
    if (node.left) { // 左节点存在
      stack.push(node.left);
      paths.push(path);
    }
  }
  return res;
};  

十二、左叶子之和

1.题目：
计算给定二叉树的所有左叶子之和。

示例

//递归遍历
var sumOfLeftLeaves = function(root) {
    //采用后序遍历 递归遍历
    // 1. 确定递归函数参数
    const nodesSum = function(node) {
        // 2. 确定终止条件
        if(node === null) {
            return 0;
        }
        let leftValue = nodesSum(node.left);
        let rightValue = nodesSum(node.right);
        // 3. 单层递归逻辑
        let midValue = 0;
        if(node.left && node.left.left === null && node.left.right === null) {
            midValue = node.left.val;
        }
        let sum = midValue + leftValue + rightValue;
        return sum;
    }
    return nodesSum(root);
};

//迭代遍历
var sumOfLeftLeaves = function(root) {
   //采用层序遍历
   if(root === null) {
       return null;
   }
   let queue = [];
   let sum = 0;
   queue.push(root);
   while(queue.length) {
     let node = queue.shift();
     if(node.left !== null && node.left.left === null && node.left.right === null) {
         sum+=node.left.val;
     }
     node.left && queue.push(node.left);
     node.right && queue.push(node.right);
   }
   return sum;
};

十三、找树左下角的值

1.题目：
给定一个二叉树，在树的最后一行找到最左边的值。

示例

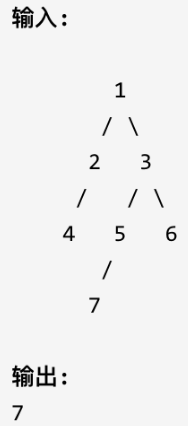
//递归遍历
var findBottomLeftValue = function(root) {
    //首先考虑递归遍历 前序遍历 找到最大深度的叶子节点即可
    let maxPath = 0, resNode = null;
    // 1. 确定递归函数的函数参数
    const dfsTree = function(node, curPath) {
    // 2. 确定递归函数终止条件
        if(node.left === null && node.right === null) {
            if(curPath > maxPath) {
            maxPath = curPath;
            resNode = node.val;
            }
        }
        node.left && dfsTree(node.left, curPath+1);
        node.right && dfsTree(node.right, curPath+1);
    }
    dfsTree(root,1);
    return resNode;
};

//层序遍历
var findBottomLeftValue = function(root) {
    //考虑层序遍历 记录最后一行的第一个节点
    let queue = [];
    if(root === null) { 
        return null;
    }
    queue.push(root);
    let resNode;
    while(queue.length) {
        let length = queue.length;
        for(let i = 0; i < length; i++) {
            let node = queue.shift();
            if(i === 0) {
                resNode = node.val;
            }
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
    }
    return resNode;
};

十四、路径总和

1.题目：
给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。
示例

示例: 给定如下二叉树，以及目标和 sum = 22，

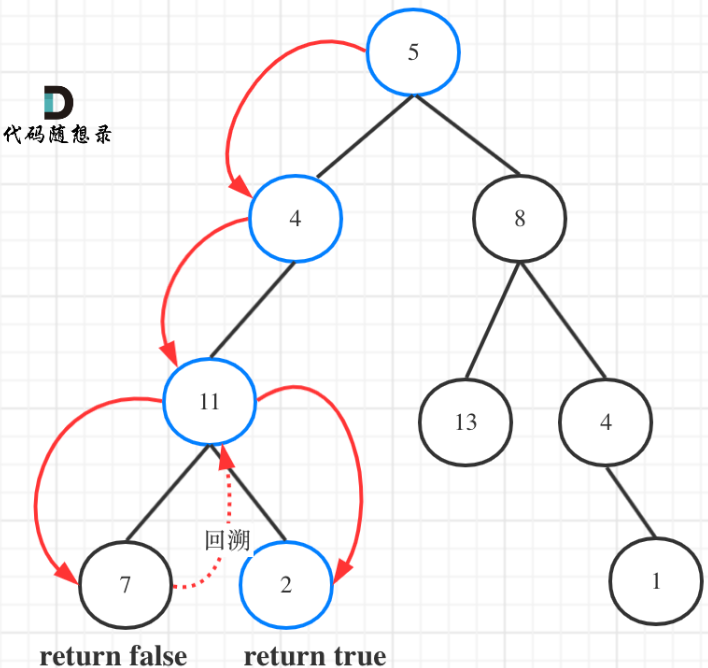
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。

//递归遍历
/**
 * @param {treenode} root
 * @param {number} targetsum
 * @return {boolean}
 */
let haspathsum = function (root, targetsum) {
  // 递归法
  const traversal = (node, cnt) => {
    // 遇到叶子节点，并且计数为0
    if (cnt === 0 && !node.left && !node.right) return true;
    // 遇到叶子节点而没有找到合适的边(计数不为0)，直接返回
    if (!node.left && !node.right) return false;

    //  左（空节点不遍历）.遇到叶子节点返回true，则直接返回true
    if (node.left && traversal(node.left, cnt - node.left.val)) return true;
    //  右（空节点不遍历）
    if (node.right && traversal(node.right, cnt - node.right.val)) return true;
    return false;
  };
  if (!root) return false;
  return traversal(root, targetsum - root.val);

  // 精简代码:
  // if (!root) return false;
  // if (!root.left && !root.right && targetsum === root.val) return true;
  // return haspathsum(root.left, targetsum - root.val) || haspathsum(root.right, targetsum - root.val);
};

//迭代遍历
let hasPathSum = function(root, targetSum) {
    if(root === null) return false;
    let nodeArr = [root];
    let valArr = [0];
    while(nodeArr.length) {
        let curNode = nodeArr.shift();
        let curVal = valArr.shift();
        curVal += curNode.val;
        // 为叶子结点，且和等于目标数，返回true
        if (curNode.left === null && curNode.right === null && curVal === targetSum) {
            return true;
        }
        // 左节点，将当前的数值也对应记录下来
        if (curNode.left) {
            nodeArr.push(curNode.left);
            valArr.push(curVal);
        }
        // 右节点，将当前的数值也对应记录下来
        if (curNode.right) {
            nodeArr.push(curNode.right);
            valArr.push(curVal);
        }
    }
    return false;
};

十五、从中序与后序遍历序列构造二叉树

1.题目：
根据一棵树的中序遍历与后序遍历构造二叉树。

注意: 你可以假设树中没有重复的元素。

示例
例如，给出

中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3] 返回如下的二叉树：

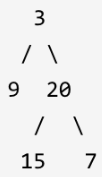
var buildTree = function(inorder, postorder) {
    if (!inorder.length) return null;
    const rootVal = postorder.pop(); // 从后序遍历的数组中获取中间节点的值， 即数组最后一个值
    let rootIndex = inorder.indexOf(rootVal); // 获取中间节点在中序遍历中的下标
    const root = new TreeNode(rootVal); // 创建中间节点
    root.left = buildTree(inorder.slice(0, rootIndex), postorder.slice(0, rootIndex)); // 创建左节点
    root.right = buildTree(inorder.slice(rootIndex + 1), postorder.slice(rootIndex)); // 创建右节点
    return root;
};

//从前序与中序遍历序列构造二叉树
var buildTree = function(preorder, inorder) {
  if (!preorder.length) return null;
  const rootVal = preorder.shift(); // 从前序遍历的数组中获取中间节点的值， 即数组第一个值
  const index = inorder.indexOf(rootVal); // 获取中间节点在中序遍历中的下标
  const root = new TreeNode(rootVal); // 创建中间节点
  root.left = buildTree(preorder.slice(0, index), inorder.slice(0, index)); // 创建左节点
  root.right = buildTree(preorder.slice(index), inorder.slice(index + 1)); // 创建右节点
  return root;
};

十六、最大二叉树

1.题目：
给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下：

• 二叉树的根是数组中的最大元素。
• 左子树是通过数组中最大值左边部分构造出的最大二叉树。
• 右子树是通过数组中最大值右边部分构造出的最大二叉树。
  通过给定的数组构建最大二叉树，并且输出这个树的根节点。

示例

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} nums
 * @return {TreeNode}
 */
var constructMaximumBinaryTree = function (nums) {
    const BuildTree = (arr, left, right) => {
        if (left > right)
            return null;
        let maxValue = -1;
        let maxIndex = -1;
        for (let i = left; i <= right; ++i) {
            if (arr[i] > maxValue) {
                maxValue = arr[i];
                maxIndex = i;
            }
        }
        let root = new TreeNode(maxValue);
        root.left = BuildTree(arr, left, maxIndex - 1);
        root.right = BuildTree(arr, maxIndex + 1, right);
        return root;
    }
    let root = BuildTree(nums, 0, nums.length - 1);
    return root;
};

十七、合并二叉树

1.题目：
给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。

你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。

示例

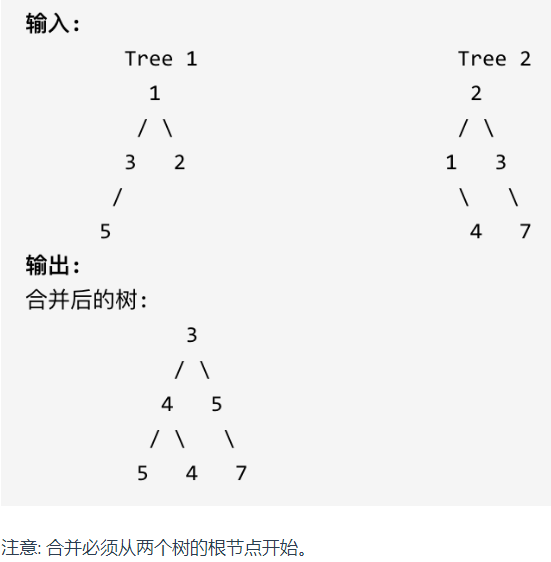
//递归法
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root1
 * @param {TreeNode} root2
 * @return {TreeNode}
 */
var mergeTrees = function (root1, root2) {
    const preOrder = (root1, root2) => {
        if (!root1)
            return root2
        if (!root2)
            return root1;
        root1.val += root2.val;
        root1.left = preOrder(root1.left, root2.left);
        root1.right = preOrder(root1.right, root2.right);
        return root1;
    }
    return preOrder(root1, root2);
};

//迭代法
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root1
 * @param {TreeNode} root2
 * @return {TreeNode}
 */
var mergeTrees = function(root1, root2) {
    if (root1 === null) return root2;
    if (root2 === null) return root1;

    let queue = [];
    queue.push(root1);
    queue.push(root2);
    while (queue.length) {
        let node1 = queue.shift();
        let node2 = queue.shift();;
        node1.val += node2.val;
        if (node1.left !== null && node2.left !== null) {
            queue.push(node1.left);
            queue.push(node2.left);
        }
        if (node1.right !== null && node2.right !== null) {
            queue.push(node1.right);
            queue.push(node2.right);
        }
        if (node1.left === null && node2.left !== null) {
            node1.left = node2.left;
        }
        if (node1.right === null && node2.right !== null) {
            node1.right = node2.right;
        } 
    }
    return root1;
};

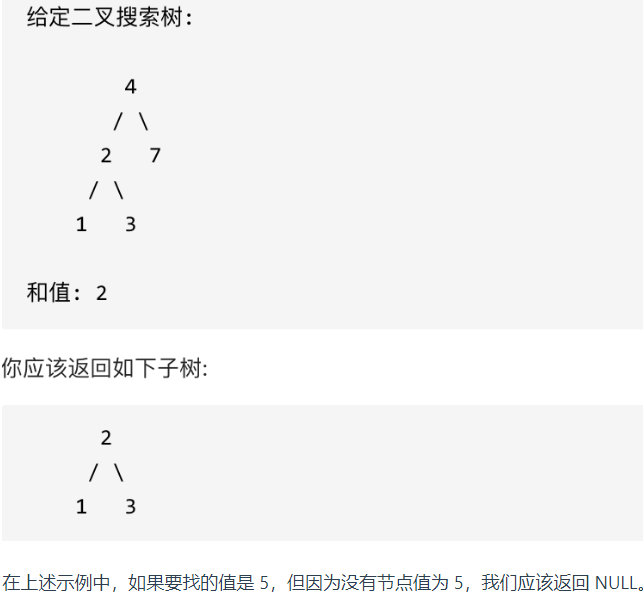
十八、二叉搜索树中的搜索

1.题目：
给定二叉搜索树（BST）的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 NULL。

示例

//递归
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} val
 * @return {TreeNode}
 */
var searchBST = function (root, val) {
    if (!root || root.val === val) {
        return root;
    }
    if (root.val > val)
        return searchBST(root.left, val);
    if (root.val < val)
        return searchBST(root.right, val);
};

//迭代
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} val
 * @return {TreeNode}
 */
var searchBST = function (root, val) {
    while (root !== null) {
        if (root.val > val)
            root = root.left;
        else if (root.val < val)
            root = root.right;
        else 
            return root;
    }
    return null;
};

十九、验证二叉搜索树

1.题目：
给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

• 节点的左子树只包含小于当前节点的数。
• 节点的右子树只包含大于当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例

//辅助数组
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isValidBST = function (root) {
    let arr = [];
    const buildArr = (root) => {
        if (root) {
            buildArr(root.left);
            arr.push(root.val);
            buildArr(root.right);
        }
    }
    buildArr(root);
    for (let i = 1; i < arr.length; ++i) {
        if (arr[i] <= arr[i - 1])
            return false;
    }
    return true;
};

//递归
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
let pre = null;
var isValidBST = function (root) {
    let pre = null;
    const inOrder = (root) => {
        if (root === null)
            return true;
        let left = inOrder(root.left);

        if (pre !== null && pre.val >= root.val)
            return false;
        pre = root;

        let right = inOrder(root.right);
        return left && right;
    }
    return inOrder(root);
};

二十、二叉搜索树的最小绝对差

1.题目：
给你一棵所有节点为非负值的二叉搜索树，请你计算树中任意两节点的差的绝对值的最小值。

示例

//递归 先转换为有序数组
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var getMinimumDifference = function (root) {
    let arr = [];
    const buildArr = (root) => {
        if (root) {
            buildArr(root.left);
            arr.push(root.val);
            buildArr(root.right);
        }
    }
    buildArr(root);
    let diff = arr[arr.length - 1];
    for (let i = 1; i < arr.length; ++i) {
        if (diff > arr[i] - arr[i - 1])
            diff = arr[i] - arr[i - 1];
    }
    return diff;
};

// 递归 在递归过程中更新最小值
var getMinimumDifference = function(root) {
    let res = Infinity
    let preNode = null
    // 中序遍历
    const inorder = (node) => {
        if(!node) return
        inorder(node.left)
        // 更新res
        if(preNode) res = Math.min(res, node.val - preNode.val)
        // 记录前一个节点         
        preNode = node
        inorder(node.right)
    }
    inorder(root)
    return res
}

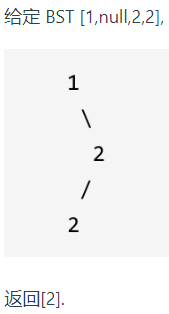
二十一、二叉搜索树的众数

1.题目：
给定一个有相同值的二叉搜索树（BST），找出 BST 中的所有众数（出现频率最高的元素）。

假定 BST 有如下定义：

• 结点左子树中所含结点的值小于等于当前结点的值
• 结点右子树中所含结点的值大于等于当前结点的值
• 左子树和右子树都是二叉搜索树

示例

//额外空间，map
var findMode = function(root) {
    // 使用递归中序遍历
    let map = new Map();
    // 1. 确定递归函数以及函数参数
    const traverTree = function(root) {
        // 2. 确定递归终止条件
        if(root === null) {
            return ;
        }
        traverTree(root.left);
         // 3. 单层递归逻辑
        map.set(root.val,map.has(root.val)?map.get(root.val)+1:1);
        traverTree(root.right);
    }
    traverTree(root);
    //上面把数据都存储到map
    //下面开始寻找map里面的
    // 定义一个最大出现次数的初始值为root.val的出现次数
    let maxCount = map.get(root.val);
    // 定义一个存放结果的数组res
    let res = [];
    for(let [key,value] of map) {
        // 如果当前值等于最大出现次数就直接在res增加该值
        if(value === maxCount) {
            res.push(key);
        }
        // 如果value的值大于原本的maxCount就清空res的所有值，因为找到了更大的
        if(value>maxCount) {
            res = [];
            maxCount = value;
            res.push(key);
        }
    }
    return res;
};

//不使用额外空间，二叉树的中序遍历
var findMode = function(root) {
    // 不使用额外空间，使用中序遍历,设置出现最大次数初始值为1
    let count = 0,maxCount = 1;
    let pre = root,res = [];
    // 1.确定递归函数及函数参数
    const travelTree = function(cur) {
        // 2. 确定递归终止条件
        if(cur === null) {
            return ;
        }
        travelTree(cur.left);
        // 3. 单层递归逻辑
        if(pre.val === cur.val) {
            count++;
        }else {
            count = 1;
        }
        pre = cur;
        if(count === maxCount) {
            res.push(cur.val);
        }
        if(count > maxCount) {
            res = [];
            maxCount = count;
            res.push(cur.val);
        }
        travelTree(cur.right);
    }
    travelTree(root);
    return res;
};

二十二、二叉树的最近公共祖先

1.题目：
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”
示例

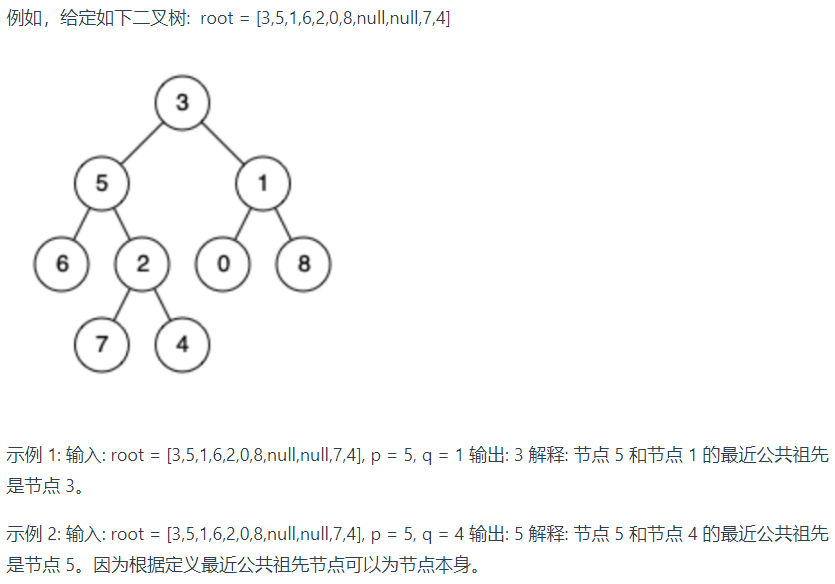
说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。

var lowestCommonAncestor = function(root, p, q) {
    // 使用递归的方法
    // 需要从下到上，所以使用后序遍历
    // 1. 确定递归的函数
    const travelTree = function(root,p,q) {
        // 2. 确定递归终止条件
        if(root === null || root === p || root === q) {
            return root;
        }
        // 3. 确定递归单层逻辑
        let left = travelTree(root.left,p,q);
        let right = travelTree(root.right,p,q);
        if(left !== null && right !== null) {
            return root;
        }
        if(left === null) {
            return right;
        }
        return left;
    }
   return  travelTree(root,p,q);
};

二十三、二叉搜索树的最近公共祖先

1.题目：
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例

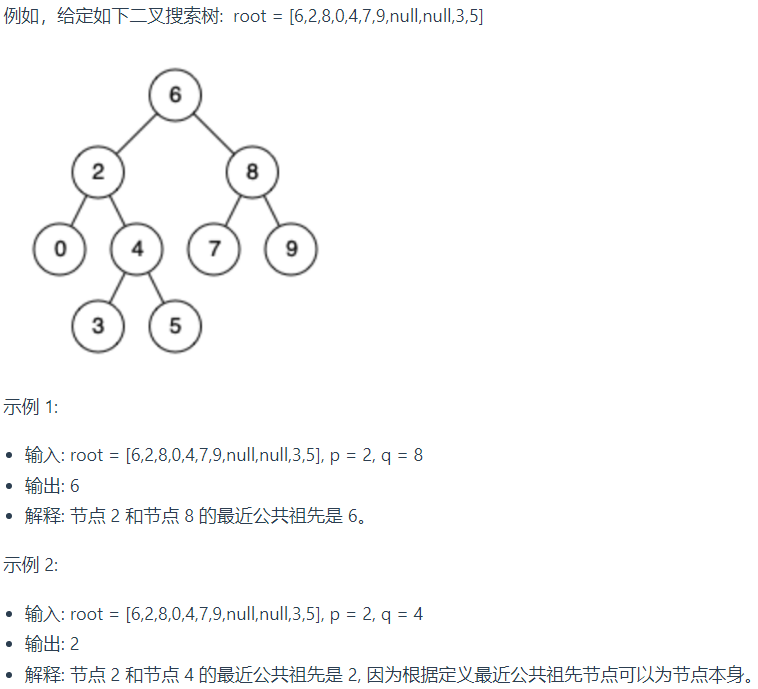
说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉搜索树中。

//递归法
var lowestCommonAncestor = function(root, p, q) {
    // 使用递归的方法
    // 1. 使用给定的递归函数lowestCommonAncestor
    // 2. 确定递归终止条件
    if(root === null) {
        return root;
    }
    if(root.val > p.val && root.val > q.val) {
        // 向左子树查询
         return root.left = lowestCommonAncestor(root.left,p,q);
    }
    if(root.val < p.val && root.val < q.val) {
        // 向右子树查询
        return root.right = lowestCommonAncestor(root.right,p,q);
    }
    return root;
};

//迭代法
var lowestCommonAncestor = function(root, p, q) {
    // 使用迭代的方法
    while(root) {
        if(root.val > p.val && root.val > q.val) {
            root = root.left;
        }else if(root.val < p.val && root.val < q.val) {
            root = root.right;
        }else {
            return root;
        }
        
    }
    return null;
};

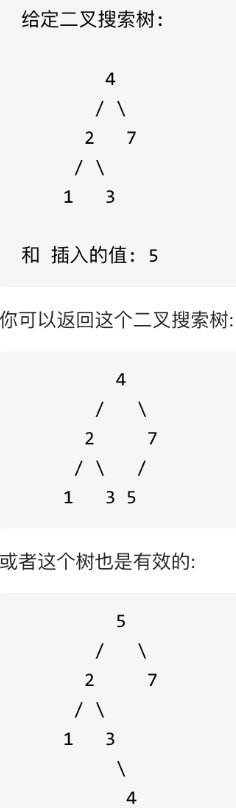
二十四、二叉搜索树中的插入操作

1.题目：
给定二叉搜索树（BST）的根节点和要插入树中的值，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据保证，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回任意有效的结果。

示例

//有返回值的递归写法
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} val
 * @return {TreeNode}
 */
var insertIntoBST = function (root, val) {
    const setInOrder = (root, val) => {
        if (root === null) {
            let node = new TreeNode(val);
            return node;
        }
        if (root.val > val)
            root.left = setInOrder(root.left, val);
        else if (root.val < val)
            root.right = setInOrder(root.right, val);
        return root;
    }
    return setInOrder(root, val);
};

//无返回值的递归
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} val
 * @return {TreeNode}
 */
var insertIntoBST = function (root, val) {
    let parent = new TreeNode(0);
    const preOrder = (cur, val) => {
        if (cur === null) {
            let node = new TreeNode(val);
            if (parent.val > val)
                parent.left = node;
            else
                parent.right = node;
            return;
        }
        parent = cur;
        if (cur.val > val)
            preOrder(cur.left, val);
        if (cur.val < val)
            preOrder(cur.right, val);
    }
    if (root === null)
        root = new TreeNode(val);
    preOrder(root, val);
    return root;
};

二十五、删除二叉搜索树中的节点

1.题目：
给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点； 如果找到了，删除它。 说明： 要求算法时间复杂度为 $O(h)$，h 为树的高度。

示例

//递归
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} key
 * @return {TreeNode}
 */
var deleteNode = function(root, key) {
    if (!root) return null;
    if (key > root.val) {
        root.right = deleteNode(root.right, key);
        return root;
    } else if (key < root.val) {
        root.left = deleteNode(root.left, key);
        return root;
    } else {
        // 场景1: 该节点是叶节点
        if (!root.left && !root.right) {
            return null
        }
        // 场景2: 有一个孩子节点不存在
        if (root.left && !root.right) {
            return root.left;
        } else if (root.right && !root.left) {
            return root.right;
        }
        // 场景3: 左右节点都存在
        const rightNode = root.right;
        // 获取最小值节点
        const minNode = getMinNode(rightNode);
        // 将待删除节点的值替换为最小值节点值
        root.val = minNode.val;
        // 删除最小值节点
        root.right = deleteNode(root.right, minNode.val);
        return root;
    }
};
function getMinNode(root) {
    while (root.left) {
        root = root.left;
    }
    return root;
}

//迭代
var deleteNode = function (root, key) {
    const deleteOneNode = target => {
        if (!target) return target
        if (!target.right) return target.left
        let cur = target.right
        while (cur.left) {
            cur = cur.left
        }
        cur.left = target.left
        return target.right
    }

    if (!root) return root
    let cur = root
    let pre = null
    while (cur) {
        if (cur.val === key) break
        pre = cur
        cur.val > key ? cur = cur.left : cur = cur.right
    }
    if (!pre) {
        return deleteOneNode(cur)
    }
    if (pre.left && pre.left.val === key) {
        pre.left = deleteOneNode(cur)
    }
    if (pre.right && pre.right.val === key) {
        pre.right = deleteOneNode(cur)
    }
    return root
}

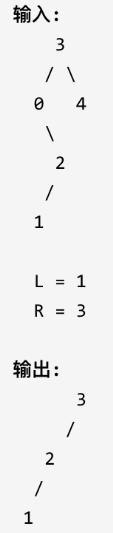
二十六、修剪二叉搜索树

1.题目：
给定一个二叉搜索树，同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树，使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点，所以结果应当返回修剪好的二叉搜索树的新的根节点。

示例

//递归
var trimBST = function (root,low,high) {
    if(root === null) {
        return null;
    }
    if(root.val < low) {
        let right = trimBST(root.right, low, high);
        return right;
    }
    if(root.val > high) {
        let left = trimBST(root.left, low, high);
        return left;
    }
    root.left = trimBST(root.left, low, high);
    root.right = trimBST(root.right, low, high);
    return root;
 }

//迭代
var trimBST = function(root, low, high) {
   if(root === null) {
       return null;
   }
   while(root !== null && (root.val < low || root.val > high)) {
       if(root.val < low) {
           root = root.right;
       }else {
           root = root.left;
       }
   }
   let cur = root;
   while(cur !== null) {
       while(cur.left && cur.left.val < low) {
           cur.left = cur.left.right;
       }
       cur = cur.left;
   }
   cur =  root;
   //判断右子树大于high的情况
   while(cur !== null) {
       while(cur.right && cur.right.val > high) {
           cur.right = cur.right.left;
       }
       cur = cur.right;
   }
   return root;
};

二十七、将有序数组转换为高度平衡二叉搜索树

1.题目：
将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
示例

//递归
var sortedArrayToBST = function (nums) {
    const buildTree = (Arr, left, right) => {
        if (left > right)
            return null;

        let mid = Math.floor(left + (right - left) / 2);

        let root = new TreeNode(Arr[mid]);
        root.left = buildTree(Arr, left, mid - 1);
        root.right = buildTree(Arr, mid + 1, right);
        return root;
    }
    return buildTree(nums, 0, nums.length - 1);
};

//迭代
var sortedArrayToBST = function(nums) {
    if(nums.length===0) {
        return null;
    }
    let root = new TreeNode(0);       //初始根节点
    let nodeQue = [root];             //放遍历的节点,并初始化
    let leftQue = [0];                //放左区间的下标,初始化
    let rightQue = [nums.length-1];   // 放右区间的下标
    
    while(nodeQue.length) {
        let curNode = nodeQue.pop();
        let left = leftQue.pop();
        let right = rightQue.pop();
        let mid = left + Math.floor((right-left)/2);
        
        curNode.val = nums[mid];      //将下标为mid的元素给中间节点
        
//         处理左区间
        if(left <= mid-1) {
            curNode.left = new TreeNode(0);
            nodeQue.push(curNode.left);
            leftQue.push(left);
            rightQue.push(mid-1);
        }
        
//         处理右区间
        if(right >= mid+1) {
            curNode.right = new TreeNode(0);
            nodeQue.push(curNode.right);
            leftQue.push(mid+1);
            rightQue.push(right);
        }
    }
    return root;
};

二十八、把二叉搜索树转换为累加树

1.题目：
给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键 小于 节点键的节点。 节点的右子树仅包含键 大于 节点键的节点。 左右子树也必须是二叉搜索树。

示例

提示：

• 树中的节点数介于 0 和 104 之间。
• 每个节点的值介于 -104 和 104 之间。
• 树中的所有值 互不相同 。
• 给定的树为二叉搜索树。

//递归
var convertBST = function(root) {
    let pre = 0;
    const ReverseInOrder = (cur) => {
        if(cur) {
            ReverseInOrder(cur.right);
            cur.val += pre;
            pre = cur.val;
            ReverseInOrder(cur.left);
        }
    }
    ReverseInOrder(root);
    return root;
};

//迭代
var convertBST = function (root) {
    let pre = 0;
    let cur = root;
    let stack = [];
    while (cur !== null || stack.length !== 0) {
        while (cur !== null) {
            stack.push(cur);
            cur = cur.right;
        }
        cur = stack.pop();
        cur.val += pre;
        pre = cur.val;
        cur = cur.left;
    }
    return root;
};

---