简介

在无障碍物的情况下，路径规划中最简单的形式，就是将路径看作是由直线段和常曲率圆弧段组成，这就是Dubins路径。Dubins路径可以简单的理解为：在最大曲率限制下，平面内两个由方向的点间的最短可行路径是 CLC 路径或 CCC 路径(C表示圆弧段，L表示直线段，CLC表示先圆弧，后直线，后圆弧)。

Dubins路径总体来说有三种基本类型，其他的可以由这三种进行组合：

1）LSL型：表示左转、直行、左转的路径，其中第一个和第三个段为左转圆弧，中间段为直线段；

2）RSR型：表示右转、直行、右转的路径，其中第一个和第三个段为右转圆弧，中间段为直线段；

3）LSR型：表示左转、直行、右转的路径，其中第一个段为左转圆弧，中间段为直线段，第三个段为右转圆弧。

L表示向左转，R表示向右转。

在给定位姿的情况下，无人机可以向左或向右转，也就是弧线段的逆时针与顺时针转。关于转弯的方向，在上面的三种基本类型中，计算时的基本计算方法，一般是以下两种：

1）含有外公切线的两个带有方向的点，不能切换转弯的方向，也就是说起始点是向右，那终止点也是向右；

2）含有内公切线的两个带有方向的点，需要切换转弯方向，如果起始点是向右，则终止点是向左。

外公切线解法与内公切线解法。

两个带有方向的点在圆弧段如果要旋转的方向是相同的，则含有外公切线，如果圆弧段的旋转方向是不同的，则含有内公切线，如下图所示：

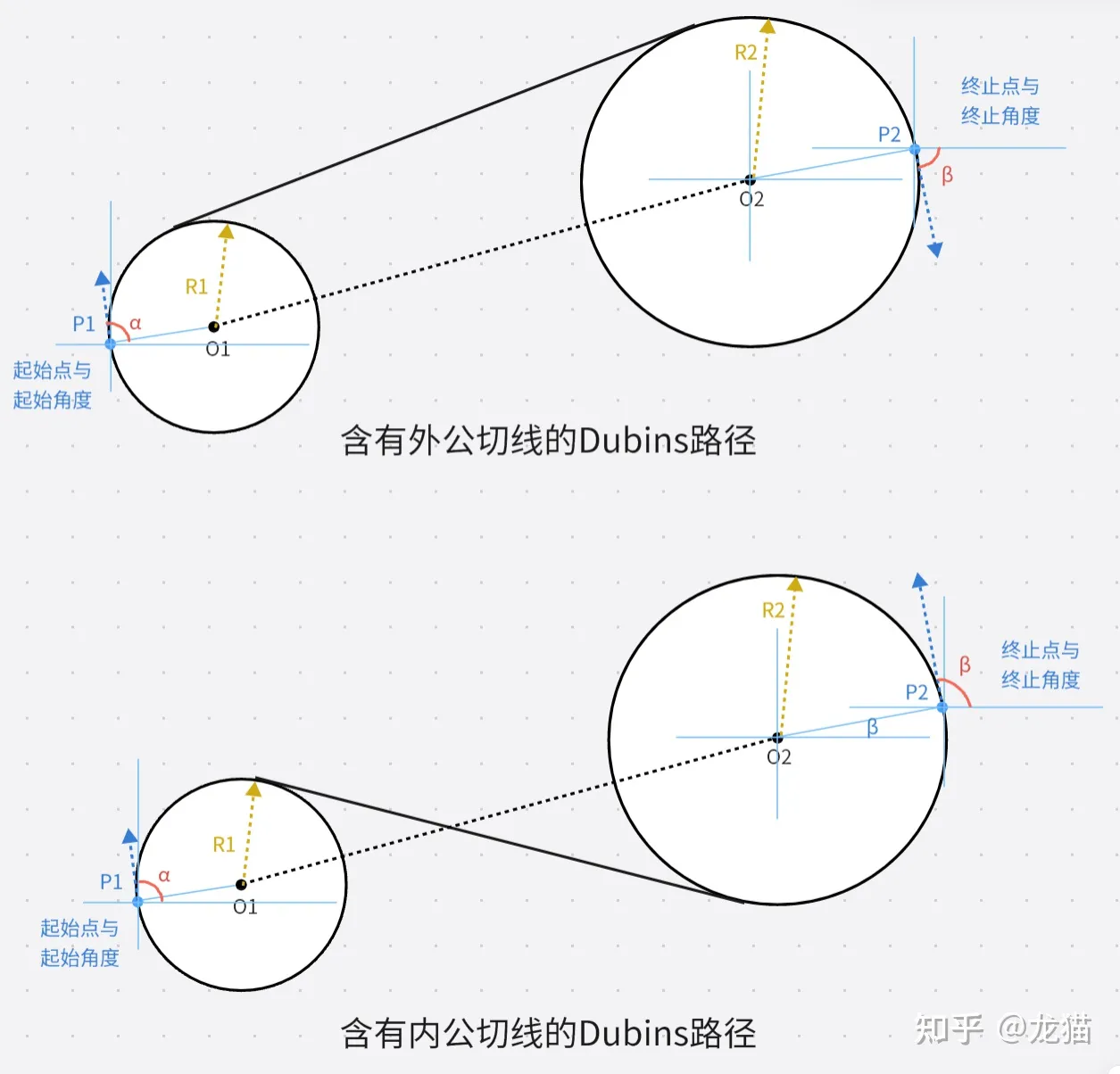
含有外公切线的两路径点，直线段路径与弧线段两圆心的连线线段不交叉，而含有内外公切线的两路径点，直线段路径与弧线段两圆心的连线线段交叉。

外公切线解

如果起始点与终止点使用的是外公切线的方式，那么要求解路径数据可按以下步骤：

1）根据运动约束，转弯半径等确定两圆弧段的半径R1，R2

2）根据起始点坐标以及起始点航向角度，转弯半径，计算起始弧线圆的圆心 O1 坐标

3）根据终止点坐标以及终止点航向角度，转弯半径，计算终止弧线圆的圆心 O2 坐标

4）计算起始圆与终止圆的切线角度

5）计算直线段的起始点与终止点坐标

这些步骤中，第4步求解切线角度会复杂一些，以下是求解过程的示意图：

1.根据起始角度α，可以求解出起始点 P1 与左侧圆心 O1 的夹角 b，∠b = ∠α ± 90°

2.之后根据角 b ，起始点 P1 以及左侧圆半径 R1，可以求解出 O1 坐标，右侧圆心 O2 坐标也可以用相同求法

3.做一个辅助圆在右侧圆 O2 上，半径是 abs(R2 - R1) ，与圆 O2 是同心圆，作一个辅助线，辅助线是辅助圆的切线，另一端连接左侧圆心 O1

4.切出点Px 与 切入点 Pn 的连线就是直线段，直线段与第 3 步做的辅助线是平行的

5.辅助圆的半径已知，为 |R2 - R1|，左右两圆的距离 d1 可以根据 O1 与 O2 的坐标计算得出，因此可以求解出 O1 到辅助圆的切线相对于 d1 的角度 a，∠a = arcsin(( |R2 - R1| ) / d1) (单位：角度)

6.根据O1，O2的坐标可以计算两者连线的角度 c，∠c = arctan( (O2.y - O1.y) / (O2.x - O1.y) )

7.根据角a，c，就可以计算出 Px 的角度 e，∠e = ∠a + ∠c + 90°

8.之后就可以计算出点 Px的坐标，Px.x = O1.x + R1 * cos(∠e) Px.y = O1.y + R1 * sin(∠e)

9.求解出了 Px 的坐标，并且已知直线段长度 d2，以及d2 的角度 ∠a+∠c，就可以计算出切入点 Pn 的坐标。

内公切线解

内公切线的情况求解路径数据的步骤与外切线解类似，也是一样的步骤，只是细节有些不同。

求解内公切线也是需要画一个辅助圆来辅助求解，不过辅助圆的半径是 R1 + R2，示意图如下：

1.根据起始点 P1 的坐标，起始角度，左圆的半径 R1，就可以求出左圆的圆心 O1 的坐标，∠e = ∠α ± 90°，O2的坐标同理求得

2.作一个辅助圆，以 O2 为圆心，半径为 R1 + R2，连接 O1 点与其在辅助圆上的切线点，记作 d2，d2与直线段 Px-Pn 平行

3.O1 与 O2 之间的距离可以计算出来，记作 d1，那么角 a 就可以计算出来 ∠a = arcsin( (R1+R2) / d1 )，d2也可以一起求解得出

4.角 b 可以通过 O1 与 O2 的坐标计算得出 ∠b = arctan( (O2.y - O1.y) / (O2.x - O1.y) )

5.∠c = 90° - ∠a，之后就可以求解出切出点 Px 的角度 = ∠c + ∠b

6.得到 Px 的角度，圆心 O1 的坐标，半径 R1，就可以求解出 Px 的坐标，之后已知 d2 的角度(∠a - ∠b)，d2的长度，就可以求解出切入点 Pn 的坐标

最终路径的选取

通常情况下，给定起始点以及起始角度，终止点以及终止角度，最多可以有四种路径方式可以完成目标，我们选取其中距离最短的即可，示意图如下：

求解四种可行路径，计算其路径长度，之后取最小值，得到最终的路径。

如果起始点与终止点的角度都是自由的，则会产生更多的路径，最多有16条，此时计算量就比较大，也是同样的思路，计算所有可行路径的长度，取最小值。