题目如下：

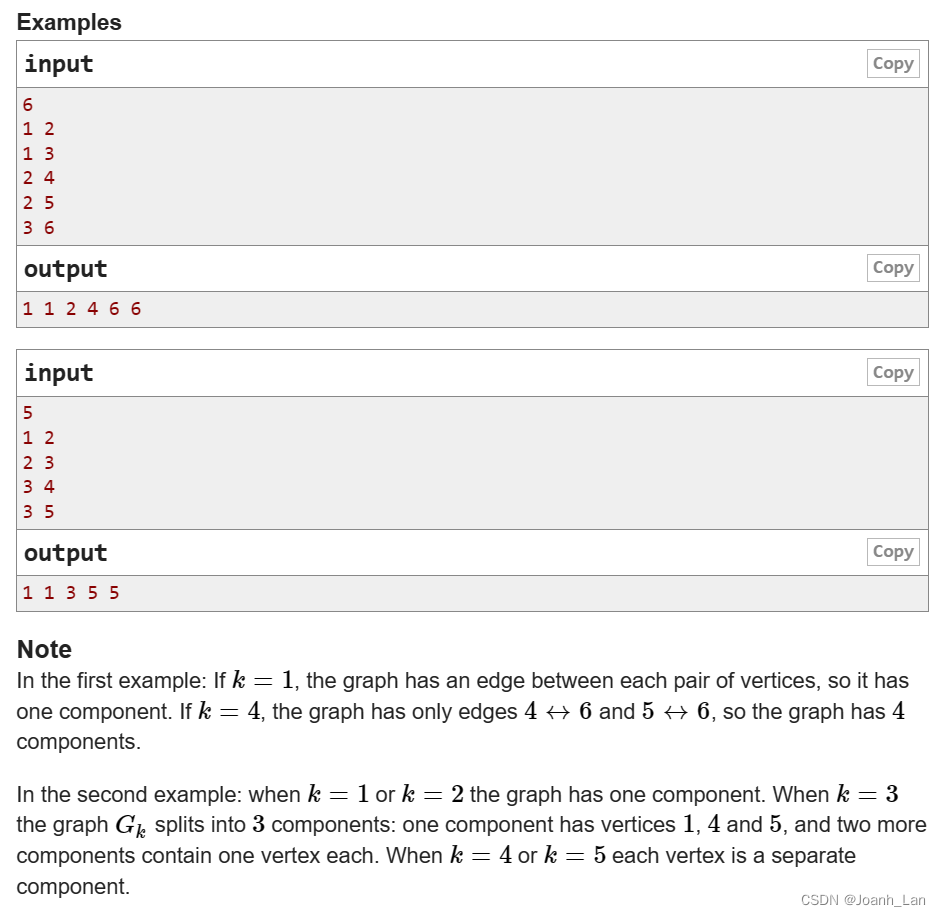
题意简说：

树上两点 $u,v$，如果 $u,v$ 的距离大于等于 $k$ 则在图 $G_k$ 上 $u,v$ 有一条无向边。
求当 $k$ 等于 [1, n] 的时候，图 $G_k$ 的连通块数量。

思路 or 题解：

我们可以先求出树的直径，记作 $mxd$, 直径的两点记作 $p,q$
我们在树上分别求出 [1, n] 到 $p，q$ 的距离取 $max$，记作 $dis[i]$
这样有什么好处？
如果 $k>mxd$ 那么$G_k$ 没有边，此时连通块的数量就是 $n$
如果 $k\le mxd$
首先 $p，q$ 一定在同一连通块中
我们还可以得出：一个点如果有边，那么一定在 $p，q$ 所在的连通块中。
我们可以通过 $dis$ 二分出小于 $k$ 的个数 $ans$
再加上 $p，q$ 所在的连通块就是答案。
所以最终答案是：$ans+1$

AC 代码如下：

/*
Make it simple and keep self stupid
author：Joanh_Lan
*/
#pragma GCC optimize(3)
#pragma GCC optimize("inline") // 如果比赛允许开编译器优化的话，可以默写这两段
#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <numeric>
#include <cstring>
#include <cmath>
#include <map>
#include <unordered_map>
#include <bitset>
#include <set>
#include <random>
#include <ctime>
#include <queue>
#include <stack>
#include <climits>
#define buff                     \
    ios::sync_with_stdio(false); \
    cin.tie(0);
// #define int long long
#define ll long long
#define PII pair<int, int>
#define px first
#define py second
typedef std::mt19937 Random_mt19937;
Random_mt19937 rnd(time(0));
using namespace std;
const int mod = 1e9 + 7;
const int inf = 2147483647;
const int N = 100009;
//int Mod(int a,int mod){return (a%mod+mod)%mod;}
//int lowbit(int x){return x&-x;}//最低位1及其后面的0构成的数值
//int qmi(int a, int k, int p){int res = 1 % p;while (k){if (k & 1) res = Mod(res * a , p);a = Mod(a * a , p);k >>= 1;}return res;}
//int inv(int a,int mod){return qmi(a,mod-2,mod);}
//int lcm(int a,int b){return a*b/__gcd(a,b);}
int n, d[N] = {-1}, deepest, dis[N];
bool st[N];
std::vector<int> g[N];
void dfs(int now, int fa)
{
	d[now] = d[fa] + 1;
	if (d[now] > d[deepest])
		deepest = now;
	for (auto it : g[now])
		if (it != fa)
			dfs(it, now);
}
void d_dfs(int u, int x)
{
	dis[u] = max(dis[u], x);
	st[u] = true;
	for (auto it : g[u])
		if (!st[it])
			d_dfs(it, x + 1);
}
void solve()
{
	cin >> n;
	for (int i = 1; i < n; i++)
	{
		int a, b;	cin >> a >> b;
		g[a].push_back(b), g[b].push_back(a);
	}
	dfs(1, 0);
	int p = deepest;
	dfs(deepest, 0);
	int q = deepest;
	int mxd = d[deepest];
	// cout << mxd << '\n';
	// cout << p << ' ' << q << '\n';
	d_dfs(p, 0);
	memset(st, 0, (n + 1));
	d_dfs(q, 0);
	// for (int i = 1; i <= n; i++)
	// 	cout << dis[i] << ' ';
	// return;
	sort(dis + 1, dis + 1 + n);
	for (int k = 1; k <= n; k++)
	{
		if (k > mxd)
		{	cout << n << ' ';	continue;}

		int l = 1, r = n, ans = 0;
		while (l <= r)
		{
			int mid = l + r >> 1;
			if (dis[mid] >= k)
				r = mid - 1;
			else
				ans = mid, l = mid + 1;
		}
		cout << ans + 1 << ' ';
	}
	cout << '\n';
}
int main()
{
	buff;
	int _ = 1;
	// cin >> _;
	while (_--)
		solve();
}