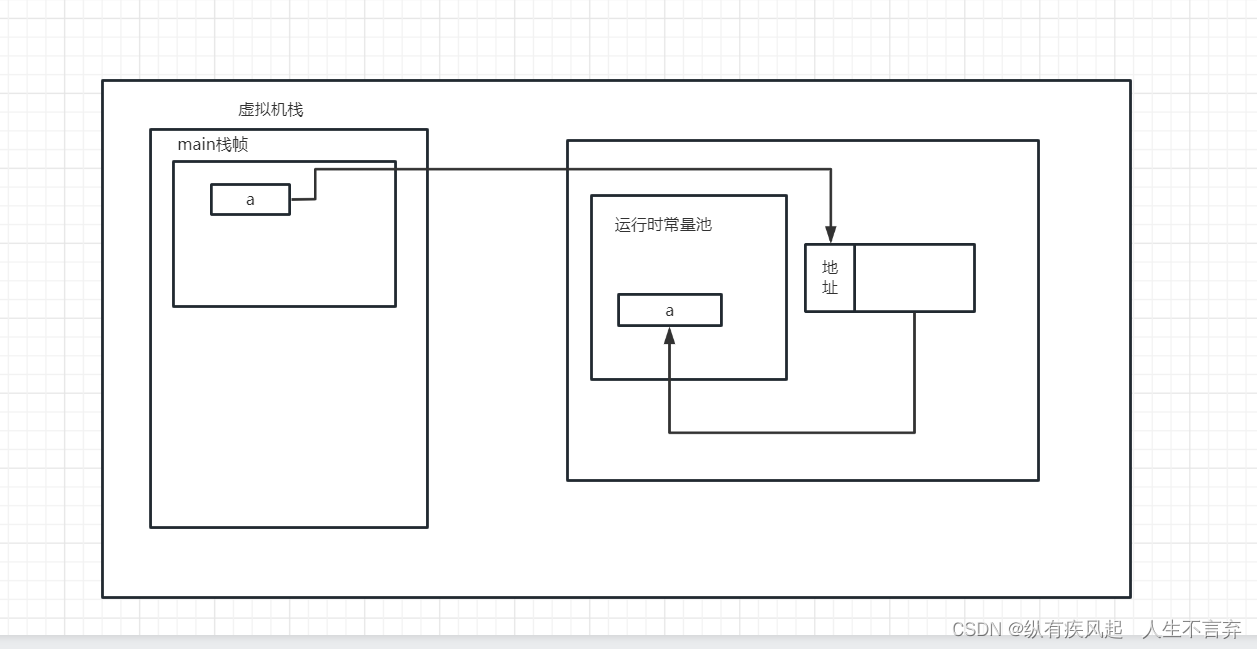
总体上，在计算机中， float 数据的的保存按照如下转换逻辑：
10进制数 >二进制数>科学计数法二进制数>c++ 条件下下浮点数在内存中的保存格式（这里面有个转换算法，需要理清楚）。

下面举出一个案例：1.125
（1）将该10进制数转成二进制，为1.001
（2）用科学计数法表示该数为：1.001*2^0
  (3)  转c++ 下浮点数的表示格式，首先介绍如下背景：

浮点型 在内存中，有3部分构成。

• 符号位（Sign bit）：占1位。0表示正数，1表示负数。
• 指数位（Exponent）：占8位，它的实际值是科学计数法中的指数+127，目的是可以让该指数位表示负数。
• 尾数位（Mantissa)：占23位。

   

 所以：
（1）该数为正数，所以，符号位为0.
（2）指数位为：2^0, 转换为内存中的模型需要+127，,所以结果为：011111111
（3）尾数为：就是科学计数法法中的1.001*2^0 中的001部分。实际就是一个常规的二进制数。直接写下来就少。
（4）所以结果就是：00111111100100000000000000000000

用附录中的工具1测试结果如下：

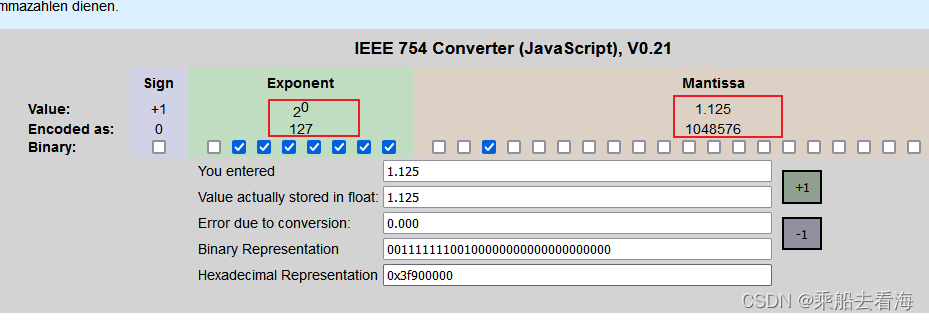
测试时可以使用如下工具：

附录：
（1）10进制转计算机保存的二进制工具：IEEE-754 Floating Point Converter
（2）进制转换器 - Codeeeee 在线工具