文章目录

动态规划
- 背包问题
- - 01背包
  - - 抽象出求解目标
    - 尝试进程子问题拆分
    - 基本情况
    - 根据拆分过程定义dp数组与转移方程
    - 遍历顺序与状态压缩
    - 模板归纳
    - 题目应用
    - 变种提升
    - - 组合问题
      - 多维01背包
      - 有特殊限制的01背包
  - 完全背包
  - - 尝试进行子问题拆分
    - 转移方程
    - 题目应用
    - 变种提升-求组合/排列数
- 打家劫舍
- - 变种提升
  - - 带有额外维度限制的打家劫舍
    - 树形打家劫舍
- 股票系列
- 子序列类
- - 最长递增子序列/子数组
- 数位dp

动态规划

背包问题

01背包

有C0-Cx件物品，每个物品价值对应为V0-Vx，有容量为N的背包，问背包能够装的最大价值。

由于每件物品只有装与不装两个状态，因此称为01背包。

抽象出求解目标

目标：C0-Cx可选，价值V0-Vx，容量为N能够装下的最大值。

尝试进程子问题拆分

子问题拆分：
假设：Cx物品选了，那么问题缩减为求解：
C0-Cx-1可选，价值V0 - Vx-1，容量为N-Vx，能够装下的最大值。
假设：Cx物品不选，那么问题缩减为求解：
C0-Cx-1可选，价值V0 - Vx-1，容量为N，能够装下的最大值。

基本情况

很显然，每件物品我们都可以按照上边的想法进行拆分求解。
当容量为0，价值为0。

根据拆分过程定义dp数组与转移方程

定义：dp[i][j]为物品0-i任意取，放进容量为j的背包中能够装的最大重量。

转移方程：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - value[i]]);

遍历顺序与状态压缩

dp[i][j]依赖它的上边和左上边的数据结果，因此，遍历顺序自上而下，自左而右。

滚动数组：由于每个数据只依赖上一行两个数据的结果，因此可以使用滚动数组来更新dp数组，由于需要的是左上方的数据和上方的数据，因此，对于背包容量我们逆序遍历时，遍历到某个位置时，此时的滚动数组就保留了左上和上的结果;
即dp[j] = max(d[j], dp[j - value[i]]);

模板归纳

枚举每个物品，逆序遍历背包，递推公式为dp[j] = max(d[j], dp[j - value[i]]);

题目应用

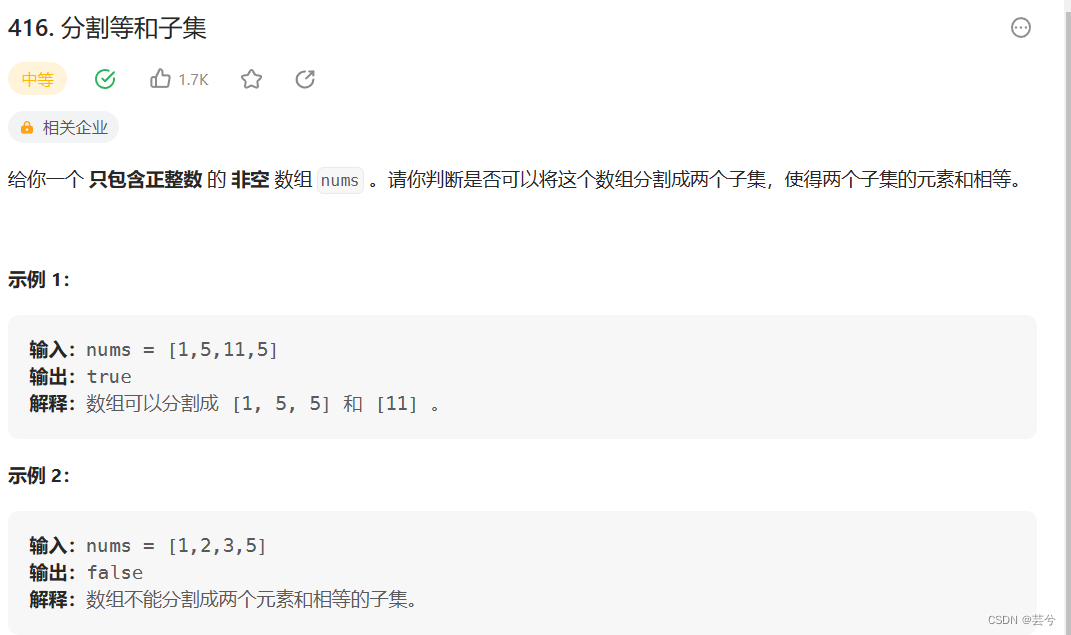
在这里插入图片描述
子集就是每个元素选或不选，最后构成的一种组合。计算数组的总和为sum，如果给定背包容量为sum / 2 能够装满，那么就存在，否则不存在。

 bool canPartition(vector<int>& nums) {
	int sum = accumulate(nums.begin(), nums.end(), 0);
	if (sum & 1) return false; // 如果sum为奇数，必不可等分
	int target = sum >> 1; // 最终要找的组合，它的累计和是nums累计和的一半。
    vector<int> dp(target + 1, 0);
	for (int num : nums) {
		for (int j = target; j >= num; --j) dp[j] = max(dp[j], dp[j - num] + num);
	}
	return dp[target] == target;
}

变种提升

组合问题

01背包还可以用于计算装满容量为N的物品的组合数。
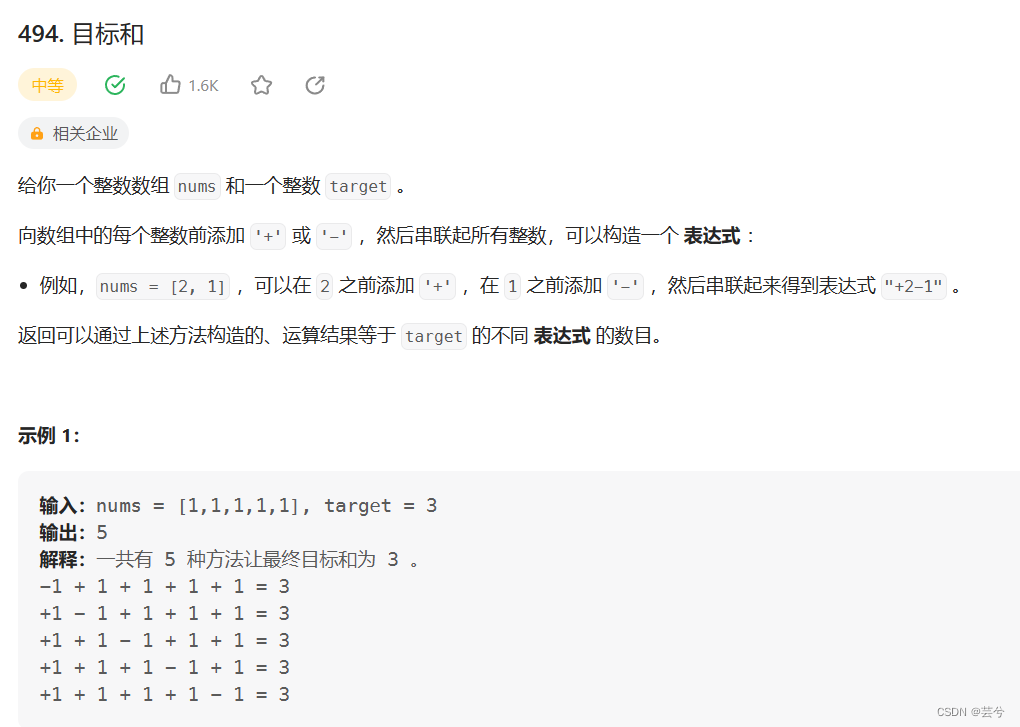
在这里插入图片描述
n个数，每个数可以是正负两种状态，不过这里要求的是组合数。

首先，由于符号未定，我们的物品是不确定的。
但是元素总和是确定的sum，
假设加法总和为x，所有元素总和为sum，那么减法元素总和为sum - x。
target = x - (sum - x) = 2x - sum
x = (sum + target) / 2

sum和target都是已知的。

因此也就是，问题可以转为装满容量为x的背包的方法数。
这样就只用考虑正数。

设dp[i][j]表示0-i元素任意选，装满j的方法数：
假设i选择：
dp[i][j] = dp[i - 1][j - nums[i]]
假设i不选：
dp[i][j] = dp[i - 1][j]

总方法数：
dp[i][j] = dp[i - 1][j - nums[i]] + dp[i - 1][j]

状态转移方程与01背包几乎一致，考虑滚动数组压缩：
dp[j] = dp[j - nums[i]] + dp[j]
进一步：
dp[j] += dp[j - nums[i]]

此外注意：求方法数时，容量为0，方法数为1，即都不选!!!。

    int findTargetSumWays(vector<int>& nums, int target) {
		int sum = accumulate(nums.begin(), nums.end(), 0);
		if (abs(target) > sum) return 0;
		if ((target + sum) % 2) return 0;
		int bagSize = (target + sum) >> 1;
		vector<int> dp(bagSize + 1);
		dp[0] = 1;
		for (int num : nums) {
			for (int j = bagSize; j >= num; --j) {
				dp[j] += dp[j - num];
			}
		} 
    }
    return dp[bagSize];

多维01背包

在这里插入图片描述
同样是子集问题，每个元素选或者不选两种情况，所不同的时，有0和1两方面的限制，即背包容量的维度是2维的。

dp[i][j][k]表示0-i物品任意选，0的容量为j，1的容量为k，能够装的物品数。
子情况拆分：
第i个选品如果选：假设第i个物品0的个数为cnt0i、1的个数为cnt1i。
dp[i][j][k] = dp[i - 1][j - cnt0i][cnt1i] + 1;
第i个物品如果不选：
dp[i][j][k] = dp[i][j][k];

转移方程和01背包一致，只依赖上方和左上方，可以逆序遍历背包容量来做成滚动数组形式;

int findMaxForm(vector<string>& strs, int m, int n) {
    vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
    for (const string &str : strs) {
        int cntOne = 0;
        for (char c : str) cntOne += c - '0';
        int cntZero = str.size() - cntOne;
        for (int i = m; i >= cntZero; --i) {
            for (int j = n; j >= cntOne; --j) {
                dp[i][j] = max(dp[i][j], dp[i - cntZero][j - cntOne] + 1);
            }
        }
    }
    return dp[m][n];
}

有特殊限制的01背包

在这里插入图片描述

这道题也是0、1背包，但是物品有主件和附件之分，每个主件可以有0,1或者2个附件，附件必须依赖主件。

有主附之分的物品是无法直接应用01背包模板的，我们需要把元素进行组装。

具体而言，一个元素的价格有四种可能，主件，主件+附件1，主件+附件2，主件+附件1+附件2。

相应的，也需要把物品的价值（即满意度进行组装）

注意点：
1、从示例2可以看出，行号为物品编号，附件可以出现在主件前，因此先用prices和values先把数据保存下来。
2、主件价格为0可以直接跳过
3、遍历每个主件时，将它与附件进行组合：主件，主件+附件1，主件+附件2，主件+附件1+附件2。
4、应用背包模板，逆序遍历背包容量。
5、输入都除10，可以降低时空复杂度，但需要注意后边输出时乘回来。

#include <bits/stdc++.h>
#include <vector>
using namespace std;

int main() {
    int N, m;
    cin >> N >> m;
    N /= 10;
    vector<vector<int>> prices(m + 1, vector<int> (4)), values (m + 1, vector<int> (4));
    // prices[i]：3个元素，分别为i号主件价格，i号主件的附件1价格，i号主件的附件2价格
    for (int i = 1; i <= m; ++i) {
        int v, p, q;
        cin >> v >> p >> q;
        v /= 10;
        p *= v;
        if (q == 0) {
            // 0 : 主件
            prices[i][0] = v;
            values[i][0] = p;
        } else {
            if (prices[q][1] == 0) {
                // 1 : 附件1
                prices[q][1] = v;
                values[q][1] = p;
            } else {
                // 2 : 附件2
                prices[q][2] = v;
                values[q][2] = p;
            }
        }
    }
    vector<int> dp(N + 1);
    for (int i = 1; i <= m; ++i) {
        if (prices[i][0] == 0) continue;
        int p1 = prices[i][0], p2 = p1 + prices[i][1], p3 = p1 + prices[i][2], p4 = p2 + p3 - p1;
        int v1 = values[i][0], v2 = v1 + values[i][1], v3 = v1 + values[i][2], v4 = v2 + v3 - v1; 
        for (int j = N; j >= p1; --j) {
            dp[j] = j >= p1 ? max(dp[j], dp[j - p1] + v1) : dp[j];
            dp[j] = j >= p2 ? max(dp[j], dp[j - p2] + v2) : dp[j];
            dp[j] = j >= p3 ? max(dp[j], dp[j - p3] + v3) : dp[j];
            dp[j] = j >= p4 ? max(dp[j], dp[j - p4] + v4) : dp[j];
        }
    }
    cout << dp[N] * 10 << endl;
    return 0;
}

完全背包

有C0-Cx种物品，每种物品价值对应为V0-Vx，每中物品的供应不限，有容量为N的背包，问背包能够装的最大价值。

完全背包与01背包的最大区别在于每种物品，01背包只有取与不取两种状态，而完全背包是不限制取的次数

仍然可以用dp[i][j]来表示0-i种物品任意选，背包容量为j，能够获取的最多的价值。

尝试进行子问题拆分

第i种物品：
不选， dp[i][j] = dp[i - 1][j]
选1件，dp[i][j] = dp[i - 1][j - wi] + vi
选2件，dp[i][j] = dp[i - 1][j - 2 ×wi] + 2×vi
……
选x件 dp[i][j] = dp[i - 1][j - x ×wi] + x×vi

因为背包容量是有限的，所以细分的种类是有限的，如果是01背包是二叉树枚举，那么完全背包就是多叉树枚举。
取上边所有情况的最大值的结果。

转移方程

01背包中我们为了使用滚动数组求解，逆序遍历背包容量，以保证求解d[j]时，dp[j - wi]是上一层的结果。

完全背包中，我们顺序遍历背包容量，对于每个物品即可实现多次取，例如，假设第一个物品，占空间为1，价值为2.
dp[1] = max(dp[1], dp[1 - 1] + 2) = 2;
dp[2] = max(dp[2], dp[2 - 1] + 2) = 4;
可以看到的dp[2]的时候是放入了两次物品1。

题目应用

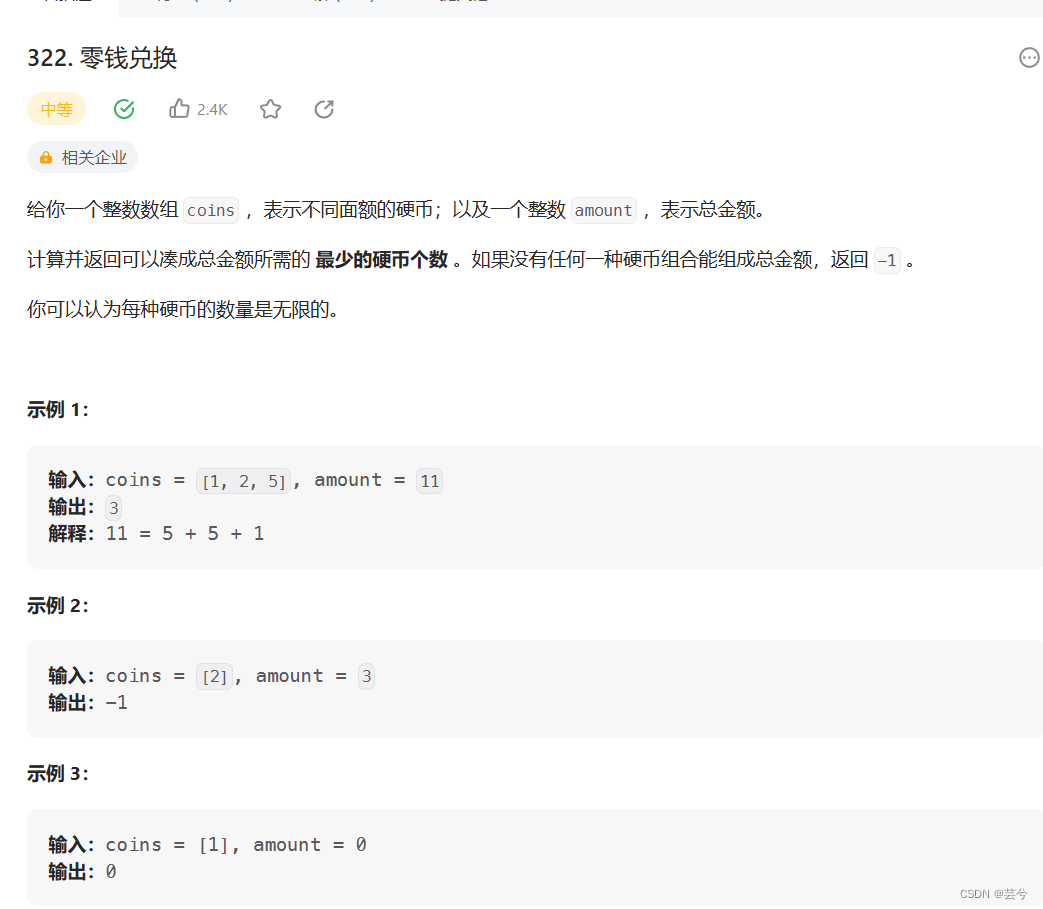
在这里插入图片描述
每个硬币无限，求构成指定目标需要的最少硬币数。

    int coinChange(vector<int>& coins, int amount) {
        vector<int> dp(amount + 1, INT_MAX); // 
        dp[0] = 0;
        for (int c : coins) {
            for (int j = c; j <= amount; ++j) {
                if (dp[j - c] != INT_MAX) {
                    dp[j] = min(dp[j], dp[j - c] + 1);
                }
            }
        }
        return dp[amount] == INT_MAX ? -1 : dp[amount];
    }

变种提升-求组合/排列数

1、使用完全背包的思路求解组合排列问题，先遍历物品后遍历背包容量得到组合数，先遍历背包容量后遍历物品，得到排列数

2、应注意遍历的起始点，内层遍历背包容量时，从coins[i]开始遍历，因为小于coins[i]的容量放不下，沿用之前的结果。内层遍历物品时，遍历范围是所有物品，但要注意，仅在j - coins[i] >= 0，即当前的容量可以放下该物品时，进行状态转移。

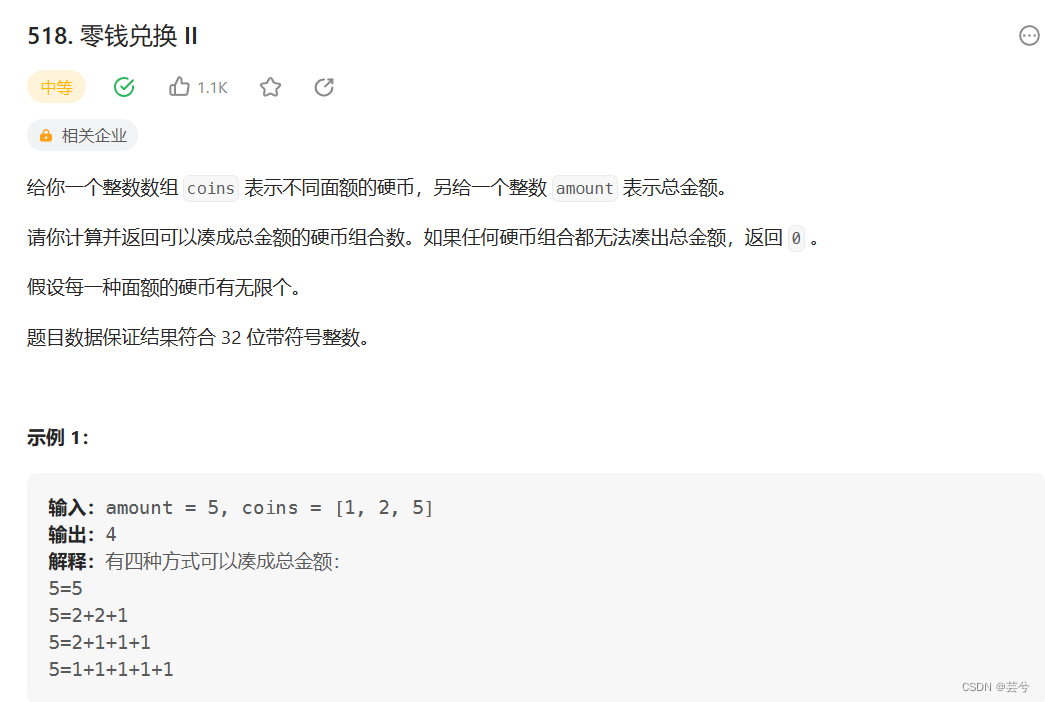
在这里插入图片描述

    int change(int amount, vector<int>& coins) {
        vector<int> dp(amount + 1, 0);
        dp[0] = 1;
        for (int c : coins) {
            for (int j = c; j <= amount; ++j) {
                dp[j] += dp[j - c];
            }
        }
        return dp[amount];
    }

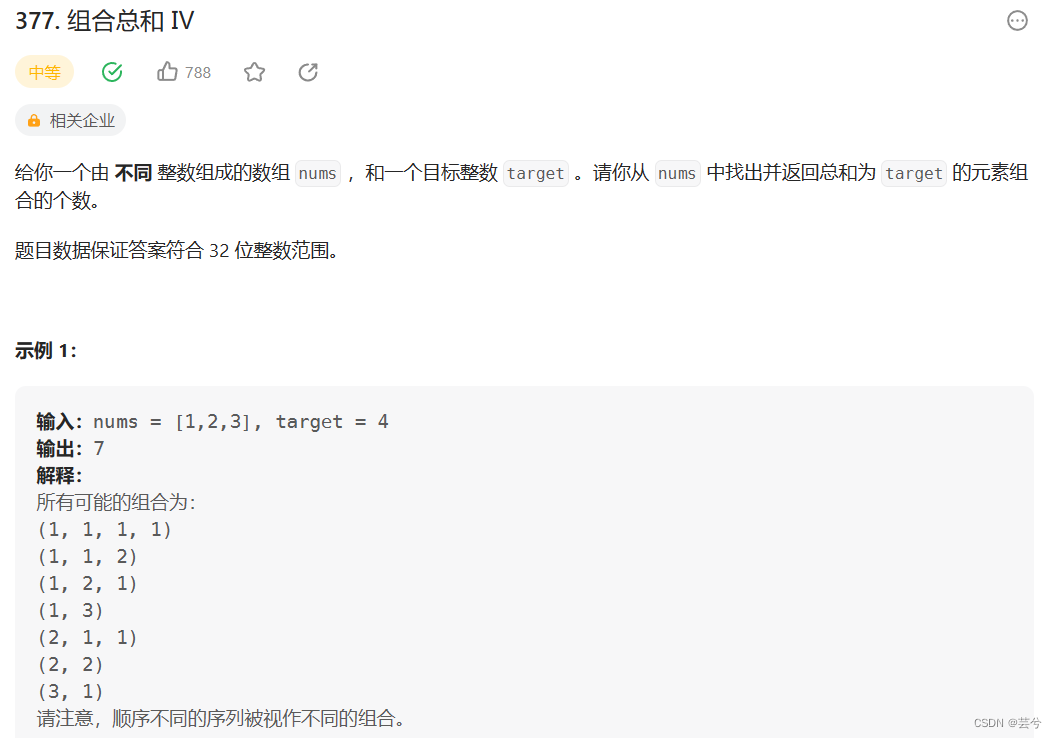
在这里插入图片描述

    int combinationSum4(vector<int>& nums, int target) {
        vector<int> dp(target + 1);
        dp[0] = 1;
        for (int j = 0; j <= target; ++j) {
            for (int n : nums) {
                if (j - n >= 0 &&  dp[j] <= INT_MAX - dp[j - n]) dp[j] += dp[j - n];
            }
        }
        return dp[target];
    }

注意：题目保证答案结果符合32位整数范围，但是我们dp表中的结果有可能不符合，会越界，但既然答案不越界，那么dp表中就没有必要记录越界的状态更新。

因此加上dp[j] <= INT_MAX - dp[j - n]只在不越界时，更新状态。

打家劫舍

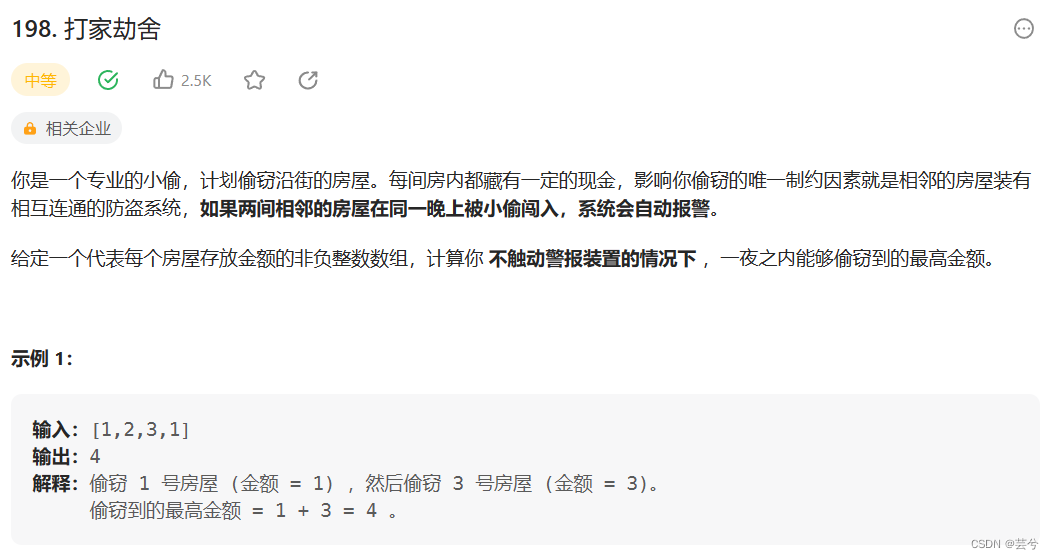
在这里插入图片描述
问题抽象：0-i个元素任意偷，不能偷相邻的，最多偷多少?
解：设最多偷dp[i]
假设第i个元素偷了，那么i-1必须不能偷，
问题缩减为：
dp[i] = vi + dp[i - 2]

假设第i个元素不偷，那么0-i-1任意偷
dp[i] = dp[i - 1];

综上 dp[i] = max(dp[i - 2] + vi, dp[i - i]);

由于仅依赖前面两个状态值，因此可以进行状态记录并转移：
初始状态都是0

    int rob(vector<int>& nums) {
        int pre1 = 0, pre2 = 0, cur = 0; // 前一个状态，前二个状态，当前状态
        for (int & n : nums) {
            cur = max(pre1, pre2 + n);
            pre2 = pre1;
            pre1 = cur;
        }
        return cur;
    }

变种提升

带有额外维度限制的打家劫舍

树形打家劫舍

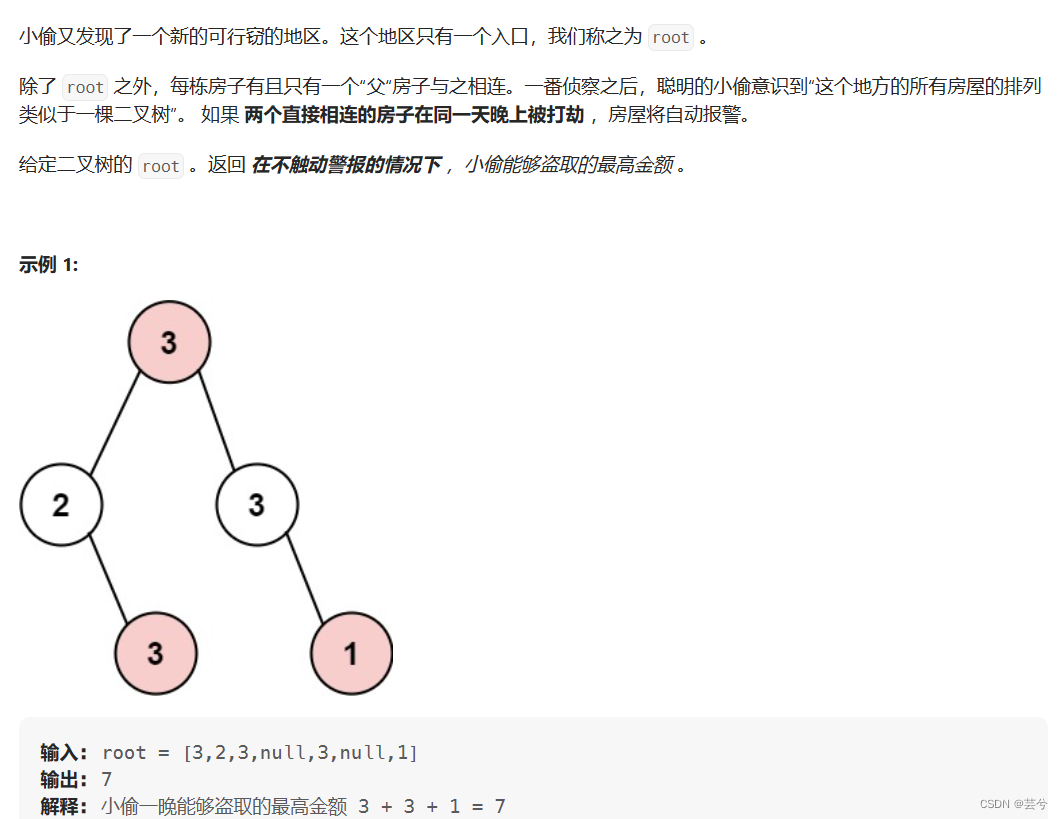
在这里插入图片描述
对于某个节点nodex：
如果选择偷，那么结果为valuex + 偷它的孩子节点的孩子节点。
如果选择不偷，那么结果为偷它的两个孩子节点。

    int rob(TreeNode* root) {
        if (!root) return 0;
        if (!root->left && !root->right) return root->val;
        int notcur = rob(root->left) + rob(root->right);
        int left = root->left ? rob(root->left->left) + rob(root->left->right) : 0;
        int right = root->right ? rob(root->right->right) + rob(root->right->left) : 0;
        int cur = root->val + left + right;
        return max(notcur, cur);
    }

以上代码超时了,我们计算了root的四个孙子（左右孩子的孩子）为头结点的子树的情况，又计算了root的左右孩子为头结点的子树的情况，计算左右孩子的时候其实又把孙子计算了一遍。

使用动态规划的思路是，我们将每个节点选或者不选的结果都返回。
如图该节点选：那么结果为valuei + 左右孩子不选的结果
如果该节点不选：那么结果为左右孩子选或者不选的最大结果之和。

    int rob(TreeNode* root) {
        pair<int, int> ans = robTree(root);
        return max(ans.first, ans.second);
    }

    pair<int, int> robTree(TreeNode* root) {
        if (!root) return {0, 0};
        pair<int, int> left = robTree(root->left);
        pair<int, int> right = robTree(root->right);
        int val0 = max(left.first, left.second) + max(right.first, right.second);
        int val1 = root->val + left.first + right.first;
        return {val0, val1};
    }