C++算法初级10——动态规划

文章目录

C++算法初级10——动态规划
- 最优化问题
- 动态规划分析流程和条件

最优化问题

生活中我们常常遇到这样一些问题：
在这里插入图片描述
看到上面的例子，我们发现这些问题都是在最大化（或者最小化）某个指标：最小化平均等待时间、最小化总旅行路程、最大化背包里的物品个数。这种类型的问题我们一般称为最优化问题。

最优化问题（optimization problem）是在一些约束下，通过进行一些决策，使得最终获益最大（或损失最小）的一类问题。

数字金字塔问题
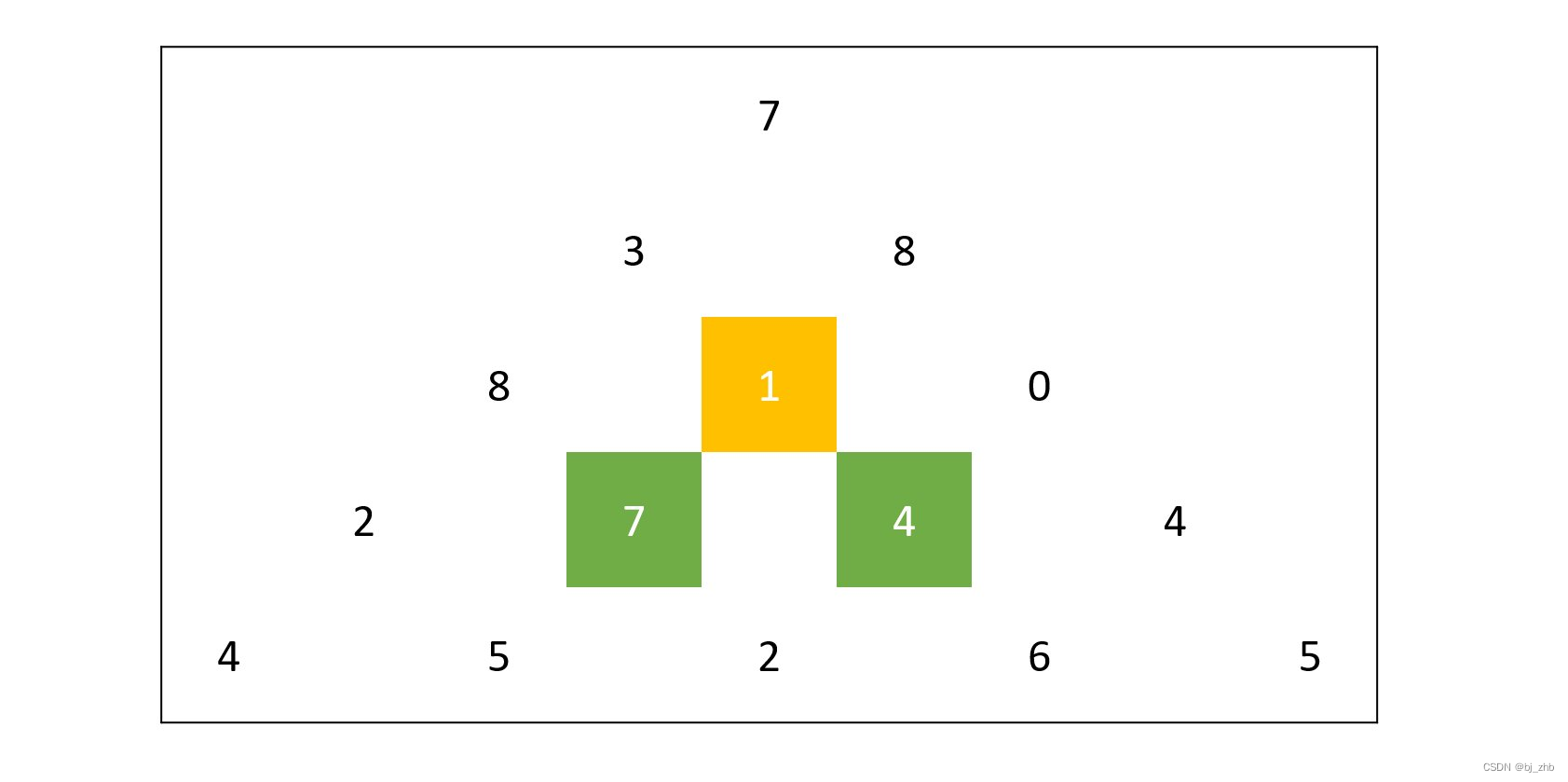
观察下面的数字金字塔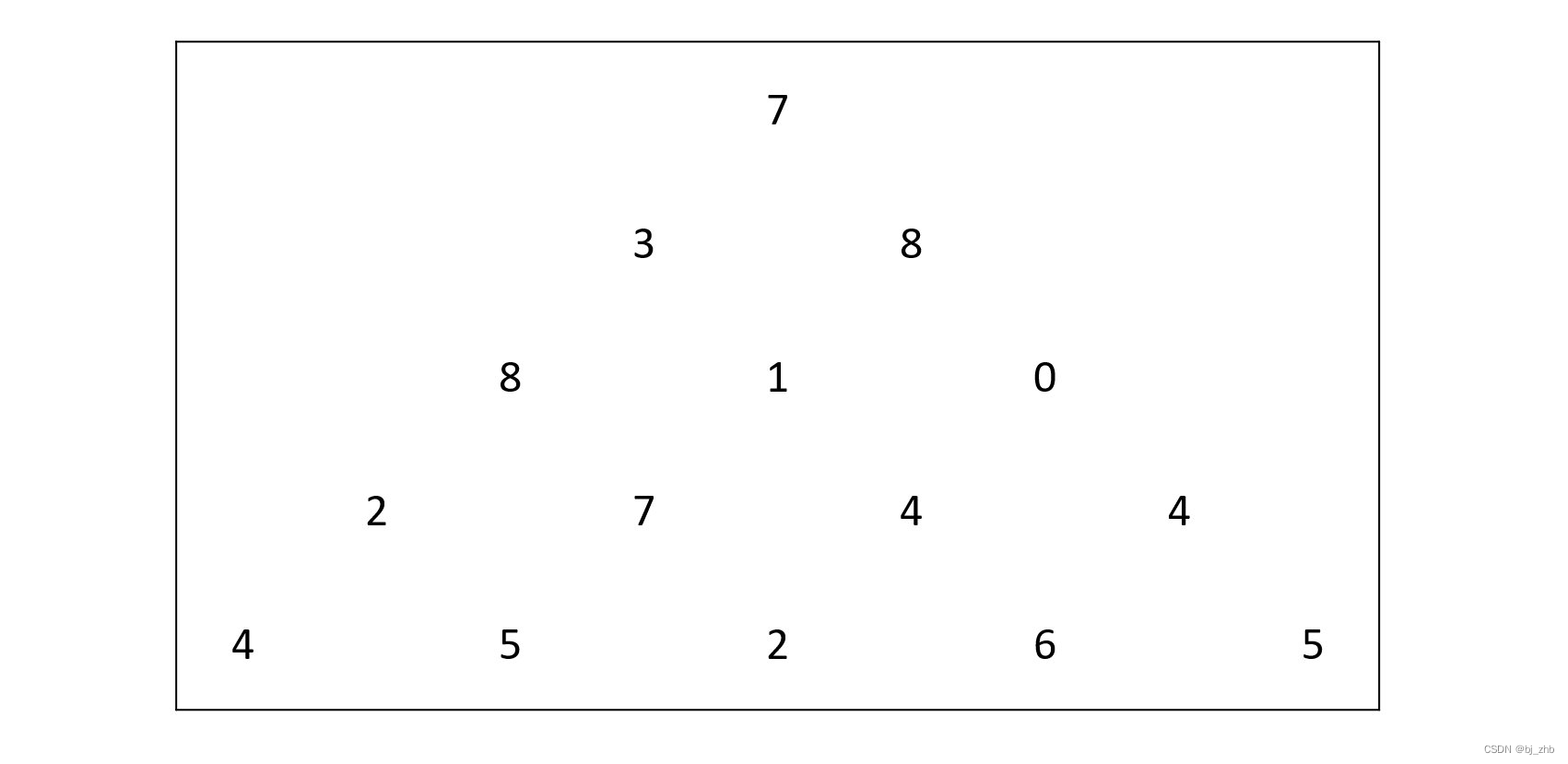：在这里插入图片描述
现在，需要我们找到一种方法，查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。

注：每一步可以走到左下方的点也可以到达右下方的点。

比如，在上面的样例中，从 7→3→8→7→5的路径经过数字的和最大。

现在，我们把数字金字塔转化成一个算法问题，就变成了：

给定一个n层的金字塔，求一条从最高点到底层任意点的路径使得路径经过的数字之和最大。

注：每一步可以走到左下方的点也可以到达右下方的点。

分析
基本思路

我们按照下面的步骤依次观察这个问题的结构：

首先，因为我们可以走到最下面一层的任意点。那么，只要我们能够分别求出到达每个点的最大路径，然后在所有点里面取最大值即可解决这个问题。
下面我们仅考虑走到最下面一层确定点的最大路径。假设我们现在想求走到最下面一层中间的2的最大路径，最暴力的方法就是列举所有走到2的路径，然后取路径和最大的一条作为答案。所以，所有走到2的路径如下：
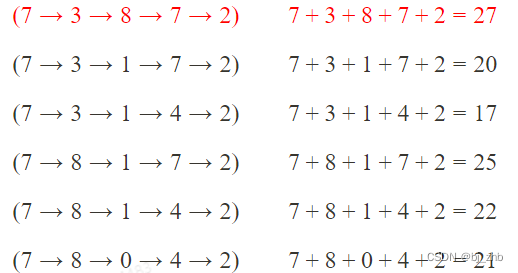
所以，最终走到2的路径里面，数字和最大是27
我们进一步观察所有走到2的路径。因为它的路径只可能从上面两个方向走下来。所以如下图，所有走到2的路径可以被分成两类：从7走过过来的路径和从4走过来的路径。

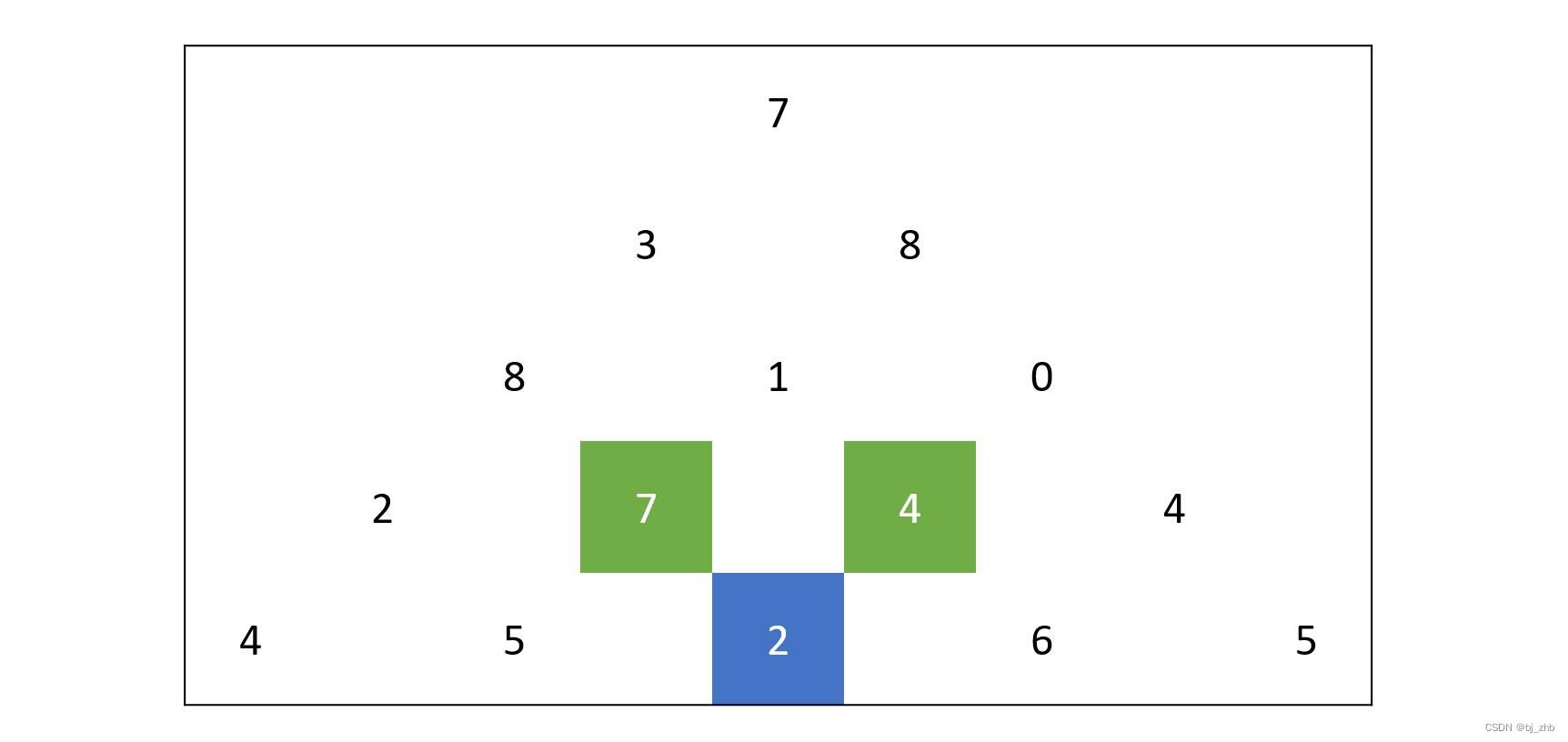
对于所有结尾是7的路径

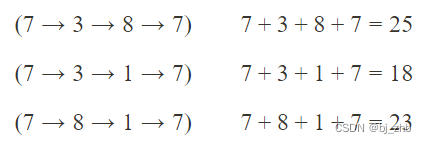
我们只需要接上一段→2，就可以变成从最上面的结点走到2的路径：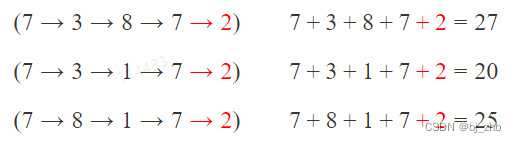
但是，如果我们已经知道“到达7的路径”里面第2条路经和第3条路径不如第1条路径，是不是就可以直接舍弃下面两条，只考虑经由第1条路径走到2的情况？也就是说，为了求所有“经由
7走到2”的路径里面，我们只需要计算第一条路径即可。
同样，对于所有“经由4走到2”的路径里面，我们也只需要挑选到达4最大的一条，然后将→2接在后面。
那么因为“从三角形顶端到达2”的路径里面，只有上面两种情况，所以，它们之间的的较大值就是到达2的最大路径，也就是 $max\{27,22\}=27$
可是如此一来，我们不需要枚举所有”从顶点到达2“的路径。但为了找出两种情况下各自的最大值，看起来我们仍需要枚举”从顶点到达7“和”从顶点到达4“的路径。

但是，我们发现，找到”从顶点到达7“和”从顶点到达4“的最大路径，就是一个和原问题”从顶点到达2“结构相似的问题！另外，由于7和4的位置比2要少一行，所以实际上，这两个问题是一个规模更小的问题！也就是说，这两个问题是原问题的一个子问题！那么，我们利用和上面类似的分析思路，就可以不用枚举所有到达7和4的路径了。

这里，我们把上一步的基本思路形式化成一个严谨的算法：

我们用a[i][j]存储数字金字塔第i行第j列的数字，用f[i][j]表示”从顶点到达第i行第j列“的所有路径中最大的数字和。
对于顶点，因为它是起始点，所以f[1][1] = a[1][1]。
因为到达(i, j)的路径最多只可能从(i - 1, j - 1)和(i - 1, j)两个点走过来（如果在三角形的最左边或者最右边，那么它的上一个结点就只有一种情况），所以，我们有下面的关系：

 f[i][j] = f[i - 1][j - 1] + a[i][j]；                    // i == j
 f[i][j] = f[i - 1][j]     + a[i][j]；                    // j == 1
 f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j]；  // otherwise

那么，观察这个等式，会发现如果我们已知f[i - 1][j - 1]和f[i - 1][j]，就可以求出f[i][j]。所以实际上，它有点像一个特殊形式的递推：有初始状态和递推关系。那么我们通过一个二重循环就可以求出所有f[i][j]。
4. 最后，我们输出所有f[n][j]对于所有(1<=j && j<=n)的最大值即可。

#include <bits/stdc++.h>
#define N 1005
#define M 110
using namespace std; 
int n = 5; // 数字金字塔有5行/* 数字金字塔:73 88 1 02 7 4 44 5 2 6 5 */
int a[N][N] = {{0}, {0, 7}, {0, 3, 8}, {0, 8, 1, 0}, {0, 2, 7, 4, 4}, {0, 4, 5, 2, 6, 5}};
int f[N][N];

int main()
{
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= i; j++)
        {
            if (i == j) // 最后一行的数字只能从上一行的最后一个数字走过来
            {
                f[i][j] = f[i - 1][j - 1] + a[i][j];
                continue;
            }
            if (j == 1) // 第一列的数字只能从上一行的第一个数字走过来
            {
                f[i][j] = f[i - 1][j] + a[i][j];
                continue;
            }
            f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j];
        }
    }
    int ans = 0;
    for (int i = 1; i <= n; i++)// 从最后一行中找最大值
        ans = max(ans, f[n][i]);
    cout << ans << endl;
    return 0;
}

动态规划过程可以进行简化
在这里插入图片描述

在这里插入图片描述

动态规划分析流程和条件

首先是动态规划分析流程：
在数字金字塔的分析中我们发现，用动态规划解决问题的过程，就是一个把原问题的过程变成一个阶段性决策的过程。

比如在数字金字塔问题中，路径每往下延伸一行，我们就进行到下一个阶段，或者步骤。而在每一个步骤里，我们需要决策到底是从左上过来，还是从右上过来。在运用动态规划方法分析问题的过程中，下面四个要素是要明确的：

状态。状态用于描述每一个步骤的参数以及结果。在数字金字塔的例子中，每个f[i][j]表示的就是一个状态。其中数组下标是当前路径的结尾，而值是以i行j列元素为结尾的所有路径中的最大值。
转移方程。转移方程用于描述不同状态之间的关系。在上面的例子中，f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j]就是一条转移方程。它描述了结尾为下一行的第j个结点的路径，和以上一行第j-1个结点和第j个结点路径之间的关系。
初始状态。初始状态描述的是整个转移方程推导的开始，是不需要经由别的状态就知道结果的状态。上面的例子中，f[1][1]=a[i][j]就是初始状态。我们以这个状态为起点，最终推导出整个三角形上每一个位置的答案。
转移方向。转移方向描述的是推导出不同状态的解的先后关系。我们之所以要明确转移方向，是因为我们不希望"已知B状态只能由A状态推到过来。但是当我们想推导B时，发现A状态的结果我们还不知道”类似的事情发生。比如由转移方程中f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j]，我们发现，如果想推导f[i][j]，必须先推导f[i - 1][j - 1]和f[i - 1][j]。所以，按照i从小到大，j从小到大的顺序推导是一种可行的推导方向。

所以，为了用动态规划解决问题，我们就需要明确上面四个方面，其中最重要的就是设计状态和转移方程。

动态规划条件
在这里指出，用动态规划求解要求我们设计出状态和转移方程，使得它们满足下面三个条件：
在这里插入图片描述

动态规划算法的关键在于解决冗余 ，这是动态规划算法的根本目的。