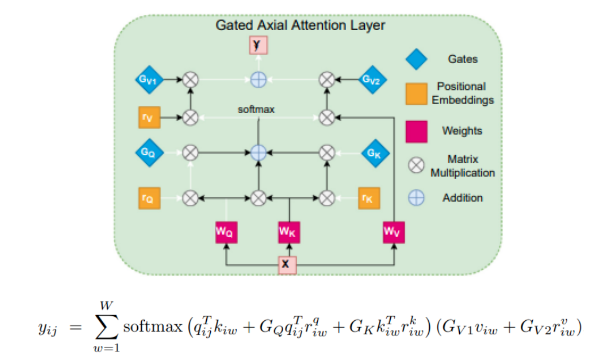
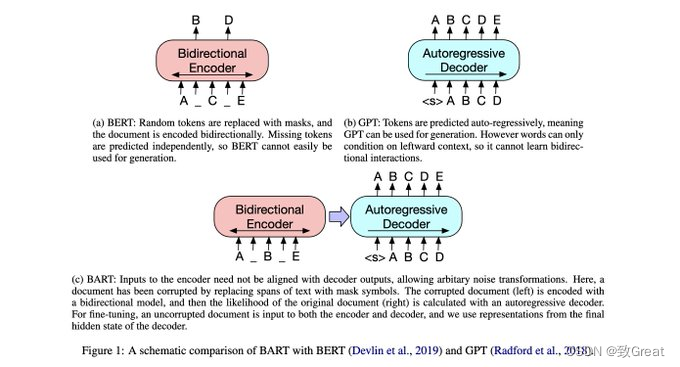
当然可以,以短时傅里叶变换STFT和WVD分析为例进行说明。
STFT得到的时频矩阵没有交叉项的干扰,但时频聚集性无法兼得;而WVD恰恰相反,其时频矩阵 能兼顾时频聚集性,但对多分量信号进行处理会产生交叉项。 为获得时频聚集性良好的时频矩阵,可以对STFT和WVD进行时频融合。
在一个时频域内,当且仅当STFT和WVD进行的时频图都存在明显时频特征,信号在该时间及频率下的能量分布才是真实的;若STFT和WVD进行的结果均不存在明显时频特征,则表明信号在该时间及频率下无能量分布;若WVD时频特征明显但是STFT在该处没有明显特征,则说明WVD中该时频特征为交叉项;若STFT中时频成分明显而WVD没有,则是因为STFT的时频聚集性不如WVD,能量过于分散。 因此可以采用适当方法进行融合,既保留WVD时频聚集性高的优势,且大大降低交叉项对后续分析的影响。

STFT时频谱

WVD时频谱

融合时频谱
此外
WVD算法虽能获得较高的时频分辨特征,但分析多成分信号时存在严重的交叉项干扰问题,限制了其实用性;而平滑伪魏格纳-维尔分布SPWVD算法虽在一定程度上抑制交叉项干扰,但降低了时频聚集度,因此可以将SPWVD和WVD相结合,利用SPWVD与WVD之间的滤波互消效应,将SPWVD二值化结果与WVD结果进行矩阵运算,最终得到高质量的时频分析结果。



知乎咨询:哥廷根数学学派
算法代码地址:mbd.pub/o/GeBENHAGEN
擅长现代信号处理(改进小波分析系列,改进变分模态分解,改进经验小波变换,改进辛几何模态分解等等),改进机器学习,改进深度学习,机械故障诊断,改进时间序列分析(金融信号,心电信号,振动信号等)