【数据挖掘与商务智能决策】第十章 支持向量机

news2024/10/5 16:22:19

1. 线性可分SVM

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

%matplotlib inline

1.1 生成模拟数据

# 导入sklearn模拟二分类数据生成模块
from sklearn.datasets import make_blobs
# 生成模拟二分类数据集
X, y =  make_blobs(n_samples=150, n_features=2, centers=2, cluster_std=1.2, random_state=40)
# 设置颜色参数
colors = {0:'r', 1:'g'}
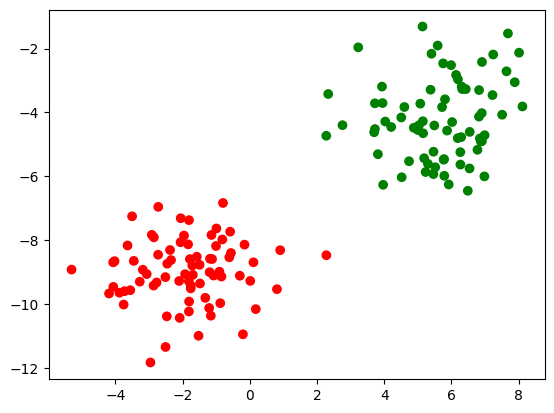
# 绘制二分类数据集的散点图
plt.scatter(X[:,0], X[:,1], marker='o', c=pd.Series(y).map(colors))
plt.show();

​
在这里插入图片描述

​

# 将标签转换为1/-1
y_ = y.copy()
y_[y_==0] = -1
y_ = y_.astype(float)

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y_, test_size=0.3, random_state=43)
print(X_train.shape, y_train.shape, X_test.shape, y_test.shape)

(105, 2) (105,) (45, 2) (45,)

1.2 线性可分支持向量机

# 导入sklearn线性SVM分类模块
from sklearn.svm import LinearSVC
# 创建模型实例
clf = LinearSVC(random_state=0, tol=1e-5)
# 训练
clf.fit(X_train, y_train)
# 预测
y_pred = clf.predict(X_test)

from sklearn.metrics import accuracy_score
# 计算测试集准确率
print(accuracy_score(y_test, y_pred))

1.0

from matplotlib.colors import ListedColormap

### 绘制线性可分支持向量机决策边界图
def plot_classifer(model, X, y):
    # 超参数边界
    x_min = -7
    x_max = 12
    y_min = -12
    y_max = -1
    step = 0.05
    # meshgrid
    xx, yy = np.meshgrid(np.arange(x_min, x_max, step),
                         np.arange(y_min, y_max, step))
    # 模型预测
    z = model.predict(np.c_[xx.ravel(), yy.ravel()])

    # 定义color map
    cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA'])
    cmap_bold = ListedColormap(['#FF0000', '#003300'])
    z = z.reshape(xx.shape)

    plt.figure(figsize=(8, 5), dpi=96)
    plt.pcolormesh(xx, yy, z, cmap=cmap_light)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold)
    plt.show()

plot_classifer(clf, X_train, y_train)

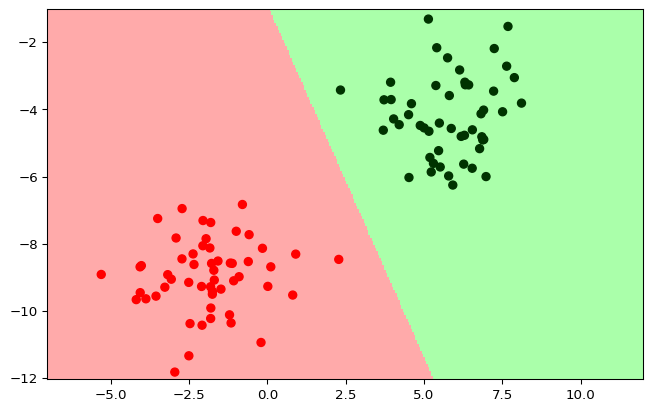
在这里插入图片描述

plot_classifer(clf, X_test, y_test)

​
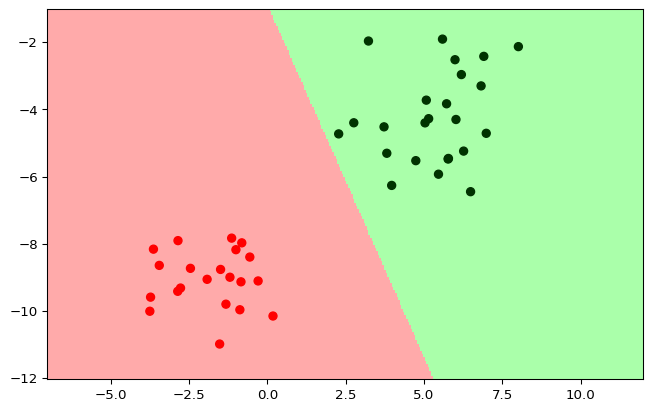
在这里插入图片描述

2. 广义线性可分SVM

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

%matplotlib inline

2.1 生成模拟数据

mean1, mean2 = np.array([0, 2]), np.array([2, 0])
covar = np.array([[1.5, 1.0], [1.0, 1.5]])
X1 = np.random.multivariate_normal(mean1, covar, 100)
y1 = np.ones(X1.shape[0])
X2 = np.random.multivariate_normal(mean2, covar, 100)
y2 = -1 * np.ones(X2.shape[0])
X_train = np.vstack((X1[:80], X2[:80]))
y_train = np.hstack((y1[:80], y2[:80]))
X_test = np.vstack((X1[80:], X2[80:]))
y_test = np.hstack((y1[80:], y2[80:]))
print(X_train.shape, y_train.shape, X_test.shape, y_test.shape)
print(X_train.shape)

(160, 2) (160,) (40, 2) (40,)
(160, 2)

# 设置颜色参数
colors = {1:'r', -1:'g'}
# 绘制二分类数据集的散点图
plt.scatter(X_train[:,0], X_train[:,1], marker='o', c=pd.Series(y_train).map(colors))
plt.show();

​
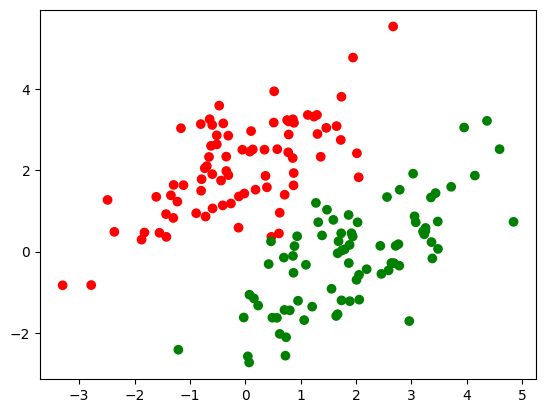
在这里插入图片描述

​

2.2 广义线性可分支持向量机

from sklearn import svm
# 创建svm模型实例
clf = svm.SVC(kernel='linear')
# 模型拟合
clf.fit(X_train, y_train)
# 模型预测
y_pred = clf.predict(X_test)

from sklearn.metrics import accuracy_score
# 计算测试集准确率
print(accuracy_score(y_test, y_pred))
# 计算测试集准确率
print('Accuracy of soft margin svm based on sklearn: ', 
      accuracy_score(y_test, y_pred))

1.0
Accuracy of soft margin svm based on sklearn:  1.0

2.3 结果可视化

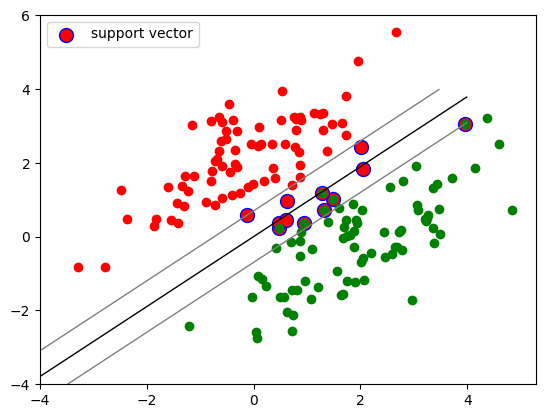
def plot_classifier(X1_train, X2_train, clf):
    plt.plot(X1_train[:,0], X1_train[:,1], "ro")
    plt.plot(X2_train[:,0], X2_train[:,1], "go")
    plt.scatter(clf.support_vectors_[:,0], clf.support_vectors_[:,1], 
                s=100, c="r", edgecolors="b", label="support vector")

    X1, X2 = np.meshgrid(np.linspace(-4,4,50), np.linspace(-4,4,50))
    X = np.array([[x1, x2] for x1, x2 in zip(np.ravel(X1), np.ravel(X2))])
    Z = clf.decision_function(X).reshape(X1.shape)
    plt.contour(X1, X2, Z, [0.0], colors='k', linewidths=1, origin='lower')
    plt.contour(X1, X2, Z + 1, [0.0], colors='grey', linewidths=1, origin='lower')
    plt.contour(X1, X2, Z - 1, [0.0], colors='grey', linewidths=1, origin='lower')
    plt.legend()
    plt.show()
    
plot_classifier(X_train[y_train==1], X_train[y_train==-1], clf)

在这里插入图片描述

3. 非线性SVM

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

%matplotlib inline

3.1 生成模拟数据

mean1, mean2 = np.array([-1, 2]), np.array([1, -1])
mean3, mean4 = np.array([4, -4]), np.array([-4, 4])
covar = np.array([[1.0, 0.8], [0.8, 1.0]])
X1 = np.random.multivariate_normal(mean1, covar, 50)
X1 = np.vstack((X1, np.random.multivariate_normal(mean3, covar, 50)))
y1 = np.ones(X1.shape[0])
X2 = np.random.multivariate_normal(mean2, covar, 50)
X2 = np.vstack((X2, np.random.multivariate_normal(mean4, covar, 50)))
y2 = -1 * np.ones(X2.shape[0])
X_train = np.vstack((X1[:80], X2[:80]))
y_train = np.hstack((y1[:80], y2[:80]))
X_test = np.vstack((X1[80:], X2[80:]))
y_test = np.hstack((y1[80:], y2[80:]))
print(X_train.shape, y_train.shape, X_test.shape, y_test.shape)

(160, 2) (160,) (40, 2) (40,)

# 设置颜色参数
colors = {1:'r', -1:'g'}
# 绘制二分类数据集的散点图
plt.scatter(X_train[:,0], X_train[:,1], marker='o', c=pd.Series(y_train).map(colors))
plt.show();

在这里插入图片描述

​

3.2 非线性SVM

from sklearn import svm
# 创建svm模型实例
clf = svm.SVC(kernel='rbf')
# 模型拟合
clf.fit(X_train, y_train)

SVC()
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org. 
SVC()
# 导入sklearn准确率评估函数
from sklearn.metrics import accuracy_score
# 模型预测
y_pred = clf.predict(X_test)
# 计算测试集准确率
print('Accuracy of soft margin svm based on cvxopt: ', 
      accuracy_score(y_test, y_pred))

Accuracy of soft margin svm based on cvxopt:  1.0

3.3 结果可视化

### 绘制非线性可分支持向量机
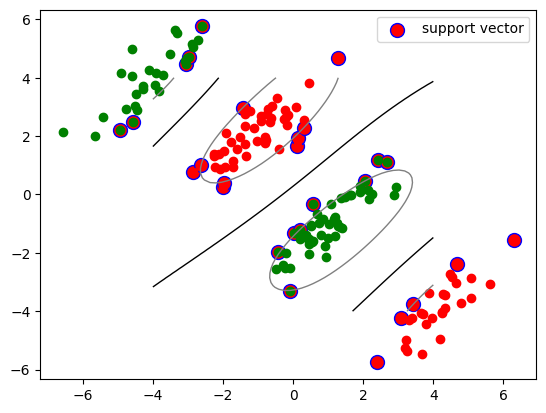
def plot_classifier(X1_train, X2_train, clf):
    plt.plot(X1_train[:,0], X1_train[:,1], "ro")
    plt.plot(X2_train[:,0], X2_train[:,1], "go")
    plt.scatter(clf.support_vectors_[:,0], clf.support_vectors_[:,1], 
                s=100, c="r", edgecolors="b", label="support vector")

    X1, X2 = np.meshgrid(np.linspace(-4,4,50), np.linspace(-4,4,50))
    X = np.array([[x1, x2] for x1, x2 in zip(np.ravel(X1), np.ravel(X2))])
    Z = clf.decision_function(X).reshape(X1.shape)
    plt.contour(X1, X2, Z, [0.0], colors='k', linewidths=1, origin='lower')
    plt.contour(X1, X2, Z + 1, [0.0], colors='grey', linewidths=1, origin='lower')
    plt.contour(X1, X2, Z - 1, [0.0], colors='grey', linewidths=1, origin='lower')
    plt.legend()
    plt.show()
    
plot_classifier(X_train[y_train==1], X_train[y_train==-1], clf)

​
在这里插入图片描述

​

4. SVR

import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline

4.1 生成模拟数据

np.random.seed(0)
X = np.sort(np.random.uniform(0,6,50),axis=0)
y = 2*np.sin(X)+0.1*np.random.randn(50)
X = X.reshape(-1,1)

4.2 SVR建模

from sklearn import svm

svr_rbf = svm.SVR(kernel='rbf',gamma=0.4,C=100)
svr_rbf.fit(X,y)

SVR(C=100, gamma=0.4)
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org. 
SVR(C=100, gamma=0.4)
svr_linear = svm.SVR(kernel='linear',C=100)
svr_linear.fit(X,y)

SVR(C=100, kernel='linear')
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org. 
SVR(C=100, kernel='linear')
svr_poly = svm.SVR(kernel='poly',degree=3,C=100)
svr_poly.fit(X,y)

SVR(C=100, kernel='poly')
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org. 
SVR(C=100, kernel='poly')

4.3 生成测试数据集

X_test = np.linspace(X.min(), 1.5*X.max(), 50)
np.random.seed(0)
y_test = 2*np.sin(X_test) + 0.1*np.random.randn(50)
X_test=X_test.reshape(-1,1)

4.4 预测并可视化

y_rbf = svr_rbf.predict(X_test)
y_linear = svr_linear.predict(X_test)
y_poly = svr_poly.predict(X_test)
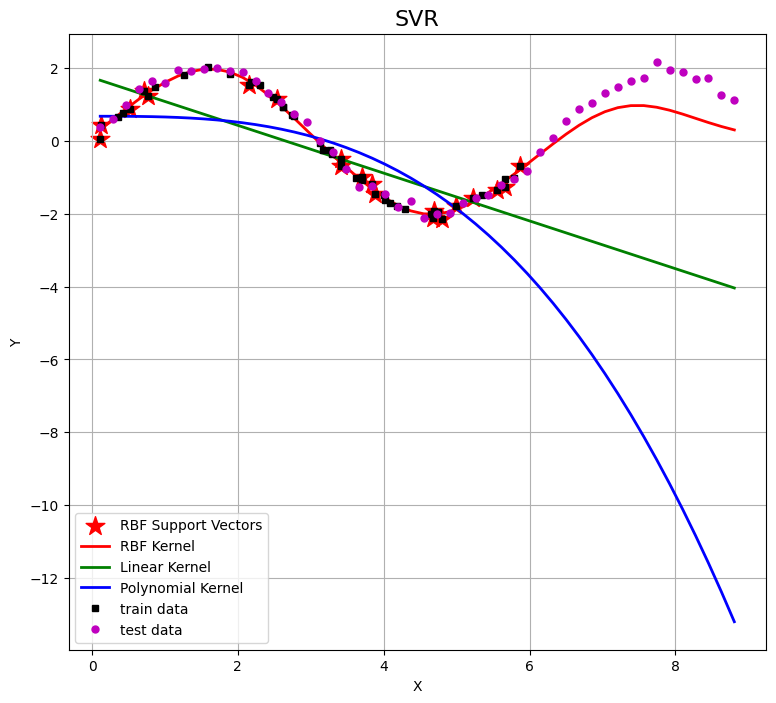
sp = svr_rbf.support_
plt.figure(figsize=(9, 8),facecolor='w')
plt.scatter(X[sp], y[sp], s=200, c='r', marker='*', label='RBF Support Vectors')
plt.plot(X_test, y_rbf, 'r-', linewidth=2, label='RBF Kernel')
plt.plot(X_test, y_linear, 'g-', linewidth=2, label='Linear Kernel')
plt.plot(X_test, y_poly, 'b-', linewidth=2, label='Polynomial Kernel')
plt.plot(X, y, 'ks', markersize=5, label='train data')
plt.plot(X_test, y_test, 'mo', markersize=5, label='test data')
plt.legend(loc='lower left')
plt.title('SVR', fontsize=16)
plt.xlabel('X')
plt.ylabel('Y')
plt.grid(True)
plt.show()

​
在这里插入图片描述

​

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/426231.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

SIP协议之RTP负载类型（payload type)

SIP协议之RTP负载类型（payload type)

一、RTP负载类型介绍​ 在SIP 音视频通话中，媒体数据是由RTP包携带的， RTP包中的PT字段标识了负载媒体数据的类型。如下图： 注： PT表示负载类型(Payload Type), 7 bits，即所传输的多媒体的类型 ​  不同的媒体编码…
阅读更多...
Kafka消费者组和分区再均衡

Kafka消费者组和分区再均衡

应用程序使用KafkaConsumer向Kafka订阅主题，并从订阅的Topic上接收消息。 要想知道如何从Kafka读取消息，需要先了解消费者和消费者组的概念。 1、消费者和消费者组 原因：假设我们有一个应用程序需要从一个Kafka Topic中读取消息并验证&…
阅读更多...
14Exceptional Control Flow Exceptions and Process(异常控制流，异常和进程)

14Exceptional Control Flow Exceptions and Process(异常控制流，异常和进程)

异常控制流 异常控制流出现的地方： 异常控制流（Exceptional Control Flow，ECF）是程序执行过程中由于某些特殊事件或条件而导致的控制流的改变。异常控制流通常出现在以下几种情况： 硬件异常和中断：硬件异…
阅读更多...
14天手撸交互式问答数字人直播教程-课程计划

14天手撸交互式问答数字人直播教程-课程计划

一、课程计划 二、时间安排 第01天：交互式问答数字人发展现状 从一个真实案例开始，介绍当前主流的交互式数字人平台，需求和应用场景，引入交互式数字人的交互流程和关键技术。后续整个直播系列的内容安排。 第02天：音…
阅读更多...
Nvidia Orin刷机保姆级教程

Nvidia Orin刷机保姆级教程

文章目录前言一、刷机准备二、刷机实战1.刷机文件下载2.Orin进入刷机模式2.1拔掉Orin上所有线缆2.2插上type-c线缆2.3长按Force Recovery按钮2.4通电2.5松开2号按钮进入刷机模式2.6确认是否进入刷机模式3.命令行刷机3.1安装jetpack总结前言 使用Orin有段时间了，现在…
阅读更多...
代码随想录_二叉树_leetcode236

代码随想录_二叉树_leetcode236

leetcode 236. 二叉树的最近公共祖先 236. 二叉树的最近公共祖先 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、…
阅读更多...
Windows主机信息搜集

Windows主机信息搜集

注意：一切内容仅用于信息技术分享，切勿用于其他用途，一切后果与作者无关。 前言： 通过命令执行使用cs拿到了内网的一台主机，接下来我们进行内网的信息搜集。 1、内网环境分析 内网渗透： 在拿到webshell的…
阅读更多...
机器学习——最大最小归一化

机器学习——最大最小归一化

问：写出最小最大归一化公式,并对以下数据集进行最小最大归一化。x{6.3,9.2,-0.8,0.2,3.6}答： x_{min}-0.8 x_{max}9.2 将每个数据点应用最小最大归一化公式： $x_1{6.3-(-0.8)}/{9.2-(-0.8)}0.71 $x_2{9.2-(-0.8)}/{9.2-(-0.8)}1.0 $x_3…
阅读更多...
PasteSpider之部署实际案例一则

PasteSpider之部署实际案例一则

本帖主要是介绍使用PasteSpider部署一个项目的过程，不一定会把所有问题都概括在内，但是至少是一个项目部署的完整流程和说明！ 我们以PasteCode的网站作为一个项目为例子，绑定的域名为https://www.pastecode.cn/,项目包含了api端和…
阅读更多...
ldap 组织结构如何转成多叉树？

ldap 组织结构如何转成多叉树？

工作中，ldap 服务器的对接，可以能会涉及到同步组织结构，认证，认证后处理等等，最近认证还不是我想写的刚需，继续来看看对于组织结构的想法 例如同步 AD 域的组织结构，或者是 ldap 协议的其他产品…
阅读更多...
「计算机控制系统」2. 采样与数据保持

「计算机控制系统」2. 采样与数据保持

计算机控制系统中的信号 理想采样过程的数学描述 信号的恢复与重构 文章目录计算机控制系统中的信号基础知识A/D中的信号D/A中的信号理想采样过程的数学描述采样过程的描述理想采样信号的描述Shannon采样定理信号的恢复与重构Shannon重构法信号保持重构法计算机控制系统中的信号…
阅读更多...
Java属性文件编码：处理非西欧语言字符的指南

Java属性文件编码：处理非西欧语言字符的指南

Java属性文件是一种轻量级的配置文件格式，用于在Java应用程序中存储键值对数据。在Java中，Properties类提供了一种方便的方式来读取和写入属性文件。 在Java中，属性文件通常使用ISO-8859-1字符集编码。这意味着如果您希望在属性文件中使用非…
阅读更多...
中科图新BIM+GIS数字化设计施工管理解决方案

中科图新BIM+GIS数字化设计施工管理解决方案

一、引言： 公路项目对施工质量和风险控制要求高，但涉及专业、队伍、机械等众多因素，导致施工质量与安全控制困难。必须提前应对并做好过程中的管控，信息化系统可支持记录和管理数据。 二、中科图新BIMGIS智慧施工管理平台 中科图…
阅读更多...
docker容器的相关环境及创建镜像1

docker容器的相关环境及创建镜像1

一、容器管理工具介绍 LXC 2008 是第一套完整的容器管理解决方案 不需要任何补丁直接运行在linux内核之上管理容器。创建容器慢，不方便移植 Docker 是在LXC基础上发展起来的。拥有一套容器管理生态系统 生态系统包含︰容器镜像、注册表、RESTFUL API及命令行操作界…
阅读更多...
Python算法设计 - McCarthy 91

Python算法设计 - McCarthy 91

目录一、什么是 McCarthy 91二、有什么用？三、Python算法实现四、作者Info一、什么是 McCarthy 91 McCarthy 91 是一个递归的函数表达式如下 函数的意思是当输入一个大于 100 的数字 n 时返回 n-10，而当输入一个小于等于101的数字 n 时递归的对 n 进行…
阅读更多...
QT之widget窗口标题与项目构建目标位置修改

QT之widget窗口标题与项目构建目标位置修改

文章目录widget窗口标题修改方法一，直接通过UI界面修改方法二，通过代码修改结果展示，选择其中一种方法即可构建项目生成文件目标位置修改1. 首先选择——>项目，如图所示：2.打开后选择构建设置——>编辑构建位置&…
阅读更多...
【VScode】手把手教你如何搭建C/C++开发环境

【VScode】手把手教你如何搭建C/C++开发环境

目录 1.VScode是什么 2.VScode的下载和安装 安装中文插件 3.VScode配置C/C开发环境 3.1 下载MinGW-w64 编译器套件 3.2 配置MinGW-w64 3.3 安装C/C插件 4.在VScode上编写C语言代码并编译成功 4.1打开文件夹 4.2 新建C语言文件，编写C语言代码 4.3设置C/…
阅读更多...
vue3项目中使用pinia

vue3项目中使用pinia

vuex 4pinia 小菠萝 vuex和之前vue2使用一致 1.import { createStore } from vuex 引入文件不同vue3组件setup写法vuex提供了hook //组件中操作store import { useStore } from vuex //提交mutations 进行修改 store.commit(increment), //dispatch 触发action 同步或者异步提交…
阅读更多...
【C】Process Control

【C】Process Control

系列连载 【python / C / C】 参考 《C语言程序设计（第四版）谭浩强》【C语言】C语言视频教程《郝斌 C 语言自学教程》 文章目录1 什么是流程控制2 流程控制的分类2.1 顺序执行2.2 选择执行2.3 循环执行2.3.1 for2.3.2 while2.3.3 do...while2.3.4 swi…
阅读更多...
[ 汇编语言 (一) ] —— 踩着硬件的鼓点，掌握计算机的精髓

[ 汇编语言 (一) ] —— 踩着硬件的鼓点，掌握计算机的精髓

🙌秋名山码民的主页 😂一个打过一年半的oier，写过一年多的Java，现在致力于学习iot应用的普通本科生 🎉欢迎关注🔎点赞👍收藏⭐️留言📝 🙏作者水平有限，如发现…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023