计算机控制系统中的信号
理想采样过程的数学描述
信号的恢复与重构

---

计算机控制系统中的信号

基础知识

消息：待发送的符号
信号：用于描述、记录和传输消息的物理过程
信息：包含在消息中的有效成分
信号是消息的表现形式，消息是信号的具体内容

注意连续时间信号和离散时间信号的定义：

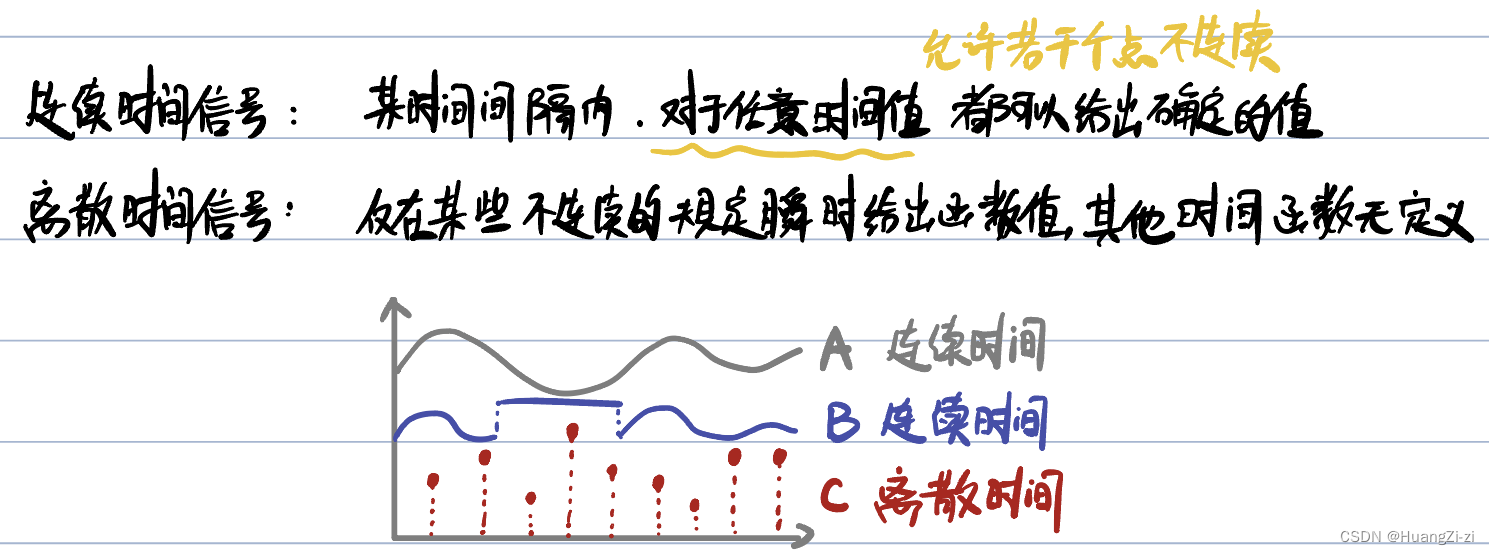
注意离散幅值信号和数字信号(二进制信号)的定义：

信号根据时间可分为离散和连续，根据幅值可分为离散、连续和二进制，总共可以组合出六种信号：

A/D中的信号

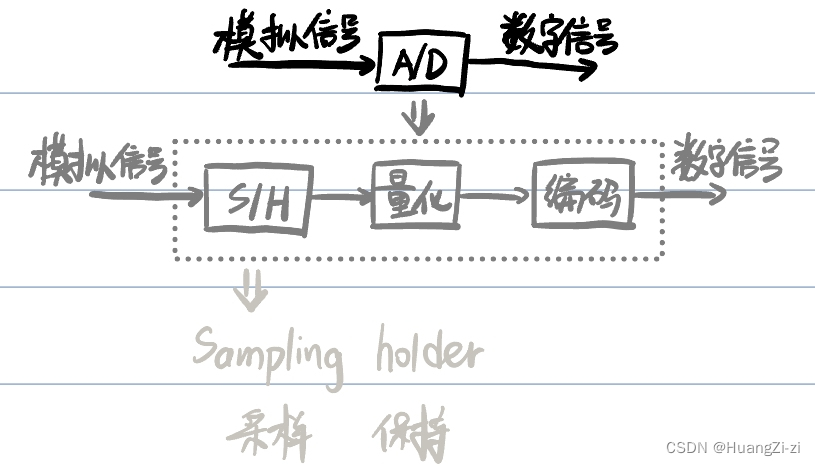
(1) 采样：把时间连续信号转变成时间离散信号
称完成信号转换的装置为采样开关
相邻两次采样之间的间隔时间称为采样周期
（我们只讨论均匀采样，即采样周期恒定不变）

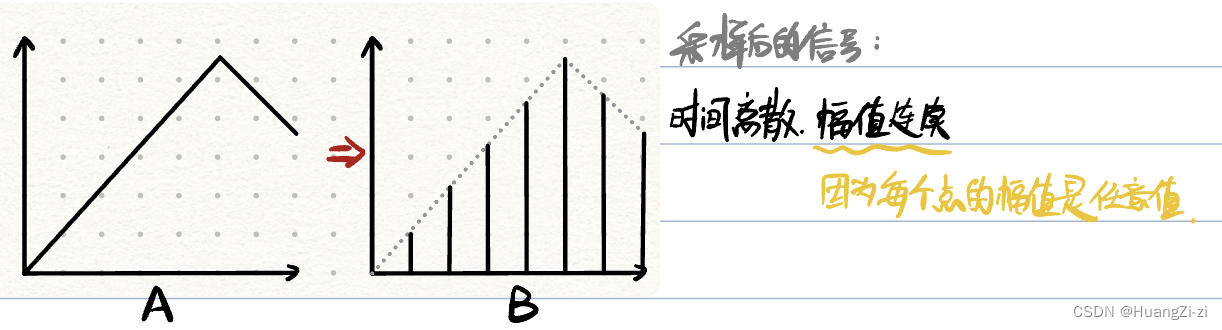
注：采样过程存在时域信息损失。采样周期一定时，已知采样前信号，可以唯一确定采样后信号。但已知采样后信号，不能唯一确定采样前信号。

(2) 量化：把采样时刻的信号幅值转变为最小量化单位的整数倍
$f(kT)=Lq$, T为采样周期，q为最小量化单位，L为整数，$k=0,1,2,\cdots$

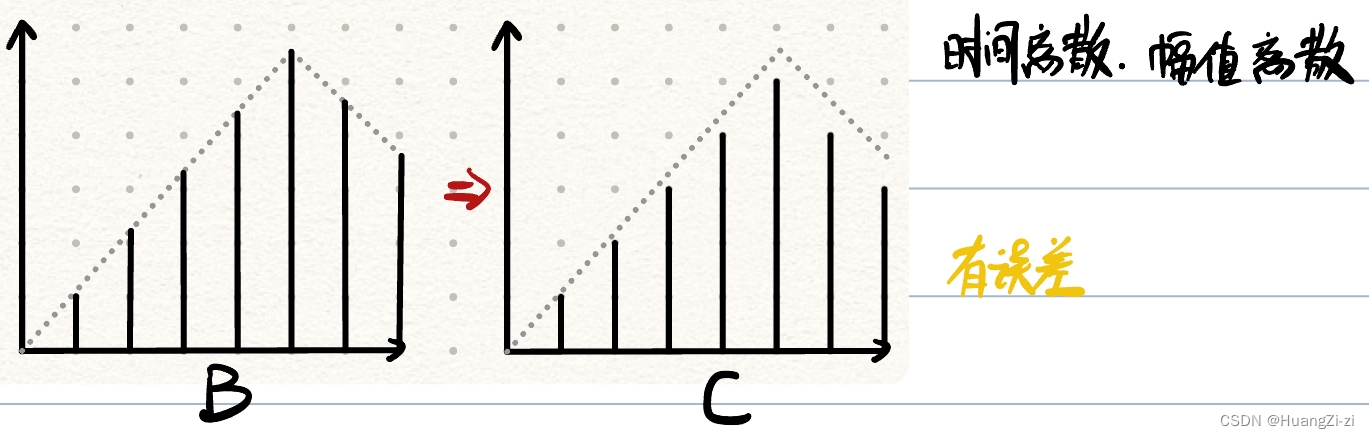
(3) 编码：将信号幅值用二进制编码表示

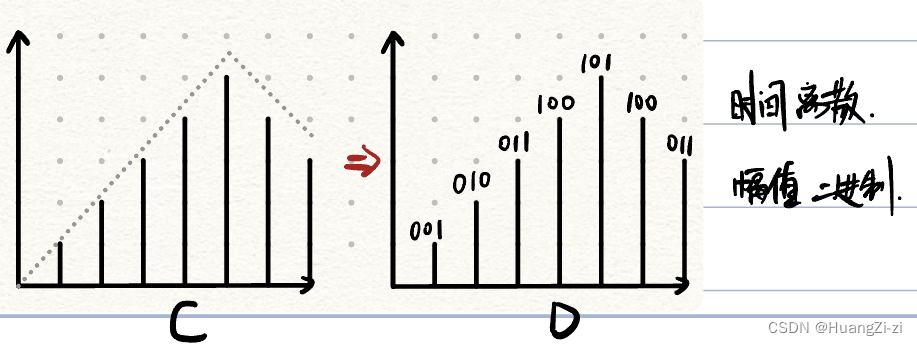
D/A中的信号

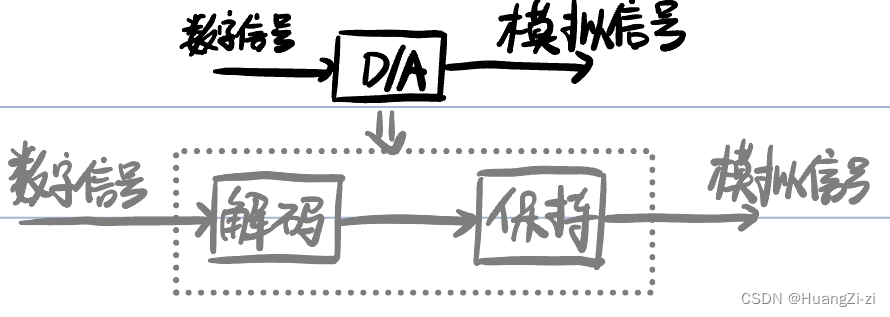
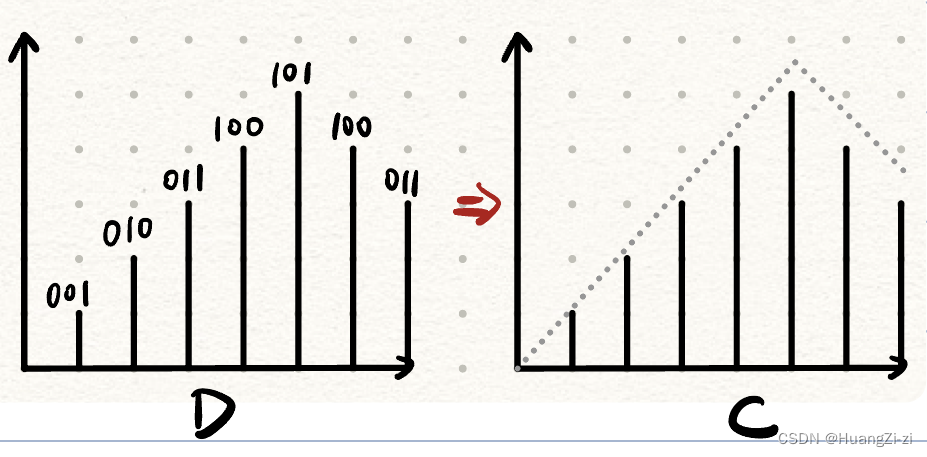
(1) 解码：将数字量转换成幅值对应的脉冲信号
把完成解码的装置称为解码器

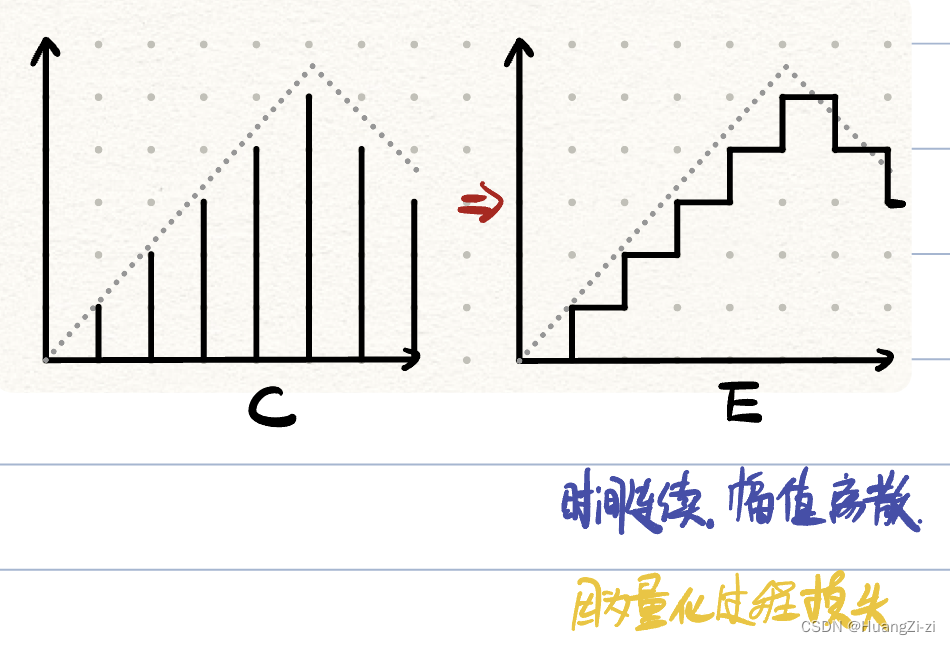
(2) 保持：把脉冲信号转换成时间连续信号
完成保持的装置称为保持器或信号恢复器

注：以上出现了ABCDE共5种信号。还有一种信号F：时间连续、幅值二进制的信号，存在于计算机内部。

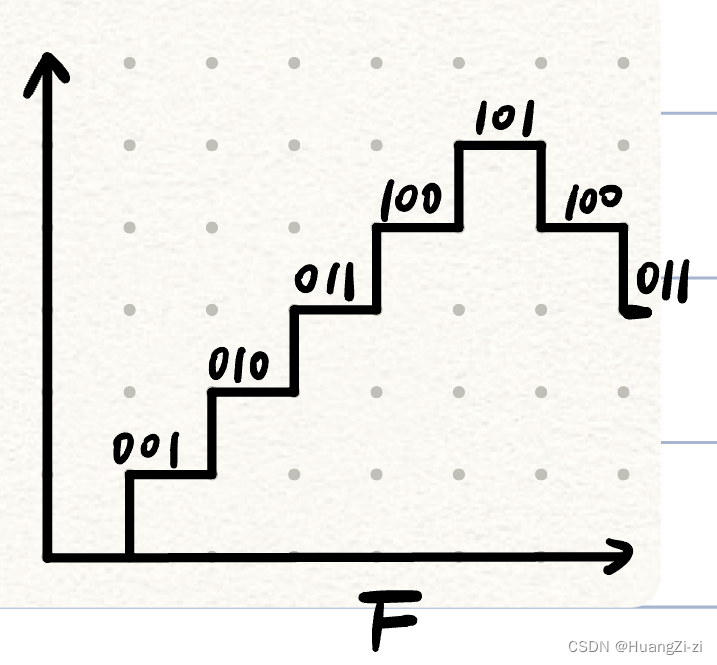
比如观察某一个内存单元，在时间上是连续的，而其内容是二进制的数字。

理想采样过程的数学描述

采样过程的描述

在方框图中，采样开关绘制为：

用*号来表示经过采样的离散信号。
描述采样过程有这几个指标：
采样周期：$T$
采样频率：$f_s=\frac{1}{T}$
采样角频率：${\omega }_s=2\pi f_s=\frac{2\pi }{T}$

理想的采样过程即是忽略采样开关的闭合时间，认为采样是在一瞬间完成的。

理想采样信号的描述

对于连续的函数$f(t)$采样，得到数字序列：$f(0),f(T),f(2T),\cdots f(kT)\cdots$
脉冲函数乘以另一个函数，相当于筛选出$t=0$时的函数值（筛选性）
利用一系列脉冲函数来筛选出间隔为T的一系列时刻的信号值：
$\begin{array}{rl}{f}^{\ast }(t)=& f(t)\delta (t)+f(t)\delta (t-T)+\cdots +f(t)\delta (t-kT)+\cdots \\ =& \sum _{k=0}^{\infty }f(t)\delta (t-kT)\\ =& f(t)\sum _{k=0}^{\infty }\delta (t-kT)\end{array}$

定义理想采样开关：${\delta }_T(t)=\sum _{k=-\infty }^{\infty }\delta (t-kT)$
一般情况下，我们认为$t<0$时，$f(t)=0$，所以理想采样开关也可以表示为：${\delta }_T(t)={\sum }_{k=0}^{\infty }\delta (t-kT)$

时域描述：
采样后的信号有以下四种表示方法：（都要认识）

• $f^{\ast }(t)=f(t){\delta }_T(t)$
• $f^{\ast }(t)=f(t){\sum }_{k=0}^{\infty }\delta (t-kT)$
• $f^{\ast }(t)={\sum }_{k=0}^{\infty }f(t)\delta (t-kT)$
• $f^{\ast }(t)={\sum }_{k=0}^{\infty }f(kT)\delta (t-kT)$

复域描述：
即是求Laplace变换：
这里要注意，采样后信号的复域描述，并不等于采样前信号复域描述的采样。必须通过以下两种方法计算：

1. 未采样时域描述 ->采样后复域描述
   $\begin{array}{rl}{F}^{\ast }(s)=& \mathcal{L}[f^{\ast }(t)]\\ =& {\int }_0^{\infty }\sum _{k=0}^{\infty }[f(t)\delta (\tau -kT)]e^{-s\tau }\mathrm{d}\tau \\ =& \sum _{k=0}^{\infty }f(kT)e^{-kTs}\end{array}$
   由于认为$t<0$时，$f(t)=0$，所以也写作：
   $F^{\ast }(s)=\sum _{k=-\infty }^{\infty }f(kT)e^{-kTs}$

2. 未采样复域描述 -> 采样后复域描述
   $F^{\ast }(s)=\frac{1}{T}\sum _{n=-\infty }^{\infty }F(s+jn{\omega }_s)$

可以看出：

• $F^{\ast }(s)$是周期函数，周期为$j{\omega }_s$
• 若$F(s)$在$s=s_1$处有一极点，那么$F^{\ast }(s)$必然在$s=s_1+jm{\omega }_s$处具有极点，$m=\pm 1,\pm 2,\cdots$
• 一采样前信号与一采样后信号相乘再采样，相当于两信号分别采样再相乘$Y^{\ast }(s)=[E^{\ast }(s)G(s){]}^{\ast }=E^{\ast }(s)[G(s){]}^{\ast }=E^{\ast }(s)G^{\ast }(s)$

频域描述：
即是求Fourier变换：
${\delta }_T(t)=\sum _{k=0}^{\infty }\delta (t-kT)$，展开成Fourier级数：${\delta }_T(t)=\frac{1}{T}\sum _{n=-\infty }^{\infty }{e}^{jn{\omega }_{s}t}$，
$f^{\ast }(t)=f(t){\delta }_T(t)=\frac{1}{T}\sum _{n=-\infty }^{\infty }f(t)e^{jn{\omega }_{s}t}$，根据频移定理：

$F^{\ast }(j\omega )=\frac{1}{T}\sum _{n=-\infty }^{\infty }F(j\omega +jn{\omega }_s)$

$n=0$时，$F^{\ast }(j\omega )=\frac{1}{T}F(j\omega )$，称为主频谱
$n\ne 0$时，相当于主频谱每隔${\omega }_s$被复制一遍。称为高频频谱

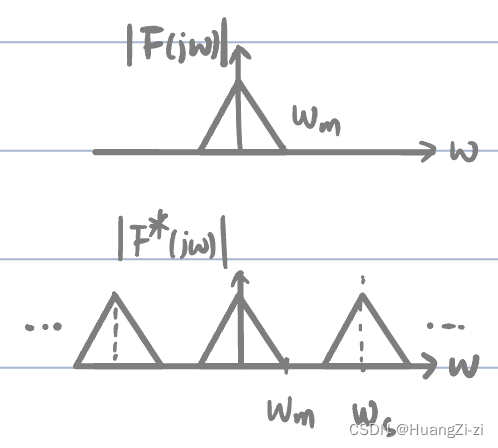
假设连续信号的频谱带宽有限（最高频率为${\omega }_m$），则采样前后信号频谱如图：

1. 下图中复制后频谱没有重叠，因为${\omega }_s-{\omega }_m>{\omega }_m$，即${\omega }_s>2{\omega }_m$。称为不发生混叠。
   
2. 下图中，${\omega }_s<2{\omega }_m$，发生混叠。
   

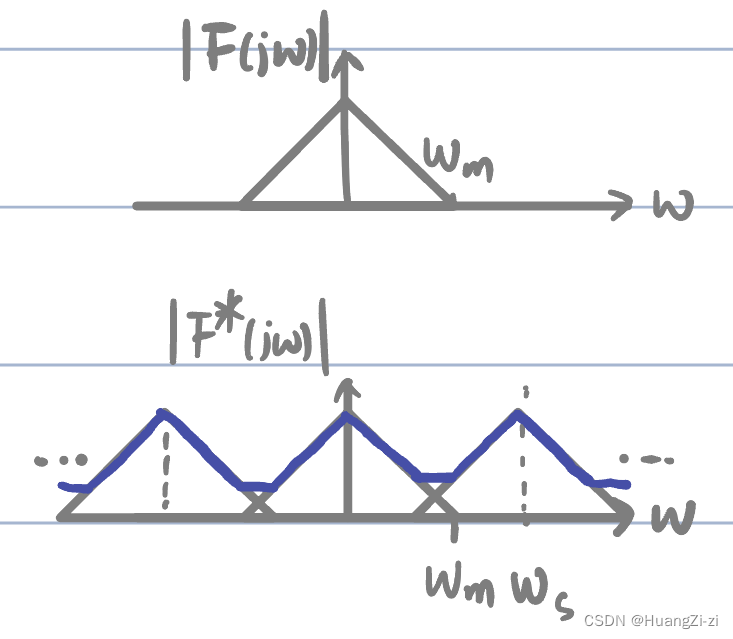
观察上面两张图，采样后信号频谱关于$\frac{n{\omega }_s}{2}$左右对称。称$\frac{{\omega }_s}{2}$这个频率为折叠频率（Nyquist频率）

Shannon采样定理

若${\omega }_m$是模拟信号$f(t)$的上限频率，${\omega }_s$为采样频率，则当${\omega }_s\ge 2{\omega }_m$时，经过采样得到的信号可以无失真地复现原信号。

这里的失真，是由于发生了混叠，高频频谱的低频部分，被叠加到主频谱的高频部分。

在实际工程中，为了防止发生混叠，常采用前置滤波器（也称抗混叠滤波器）。即在采样开关前串连一个低通滤波器，滤除高于$\frac{{\omega }_s}{2}$的频谱分量，避免发生混叠。同时，这个滤波器也有助于滤除高频干扰。

选取采样频率时，受到计算机性能的限制，不能选得太高。对于伺服系统，一般取${\omega }_s\ge 6\sim 10{\omega }_c$

信号的恢复与重构

信号重构：采样的逆过程。

Shannon重构法

无失真地复现原信号，就是采用了以下的方法：使用理想低通滤波器：
$G(j\omega )=\{\begin{array}{r}1,|\omega |\le \frac{{\omega }_s}{2}\\ 0,|\omega |>\frac{{\omega }_s}{2}\end{array}$

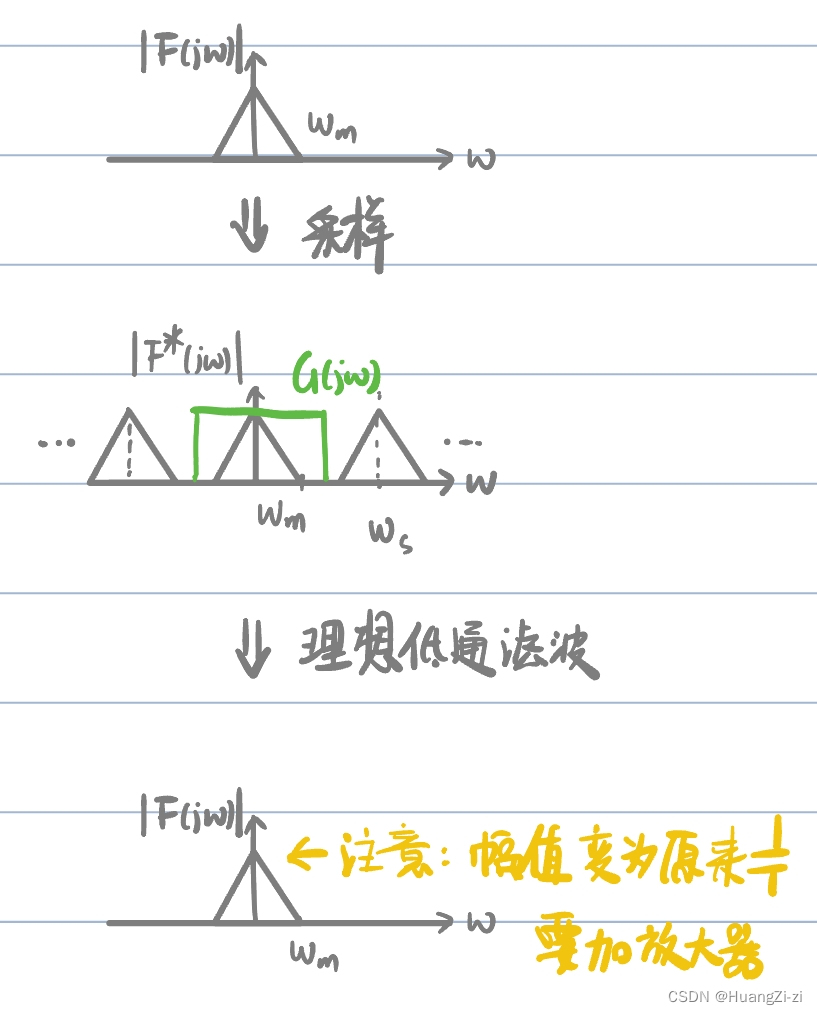
但理想低通滤波器是不存在的，因此这种方法也只是一个理想的重构过程，不能用于实际系统。

信号保持重构法

Signal Hold，使用保持器实现。
基本思想是，由过去时刻的采样值$f(kT),k\le t/T$，推出当前时刻$f(t)$的值

假设在一次采样之后，下一次采样还没到来之间的这一段时间($0<\Delta t<T$)，取:
$f(t)=f(kT+\Delta t)=a_0+a_1{\Delta }_t+a_2{\Delta }_t^2+\cdots +a_n{\Delta }_t^n$
选择阶数n，根据过去的采样值可以计算出各参数，进而计算出两次采样之间的$f(t)$值。

零阶保持器：
Zero Order Holder （ZOH）
$f(t)=f(kT+\Delta t)=f(kT)$
直观理解就是保持上一次的采样值，直到下一次采样。

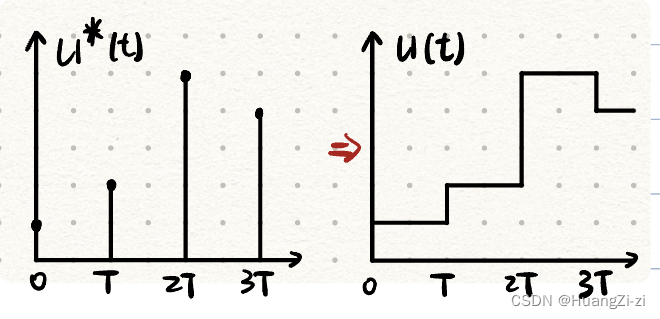
输入单位脉冲函数，输出宽度为T的矩形脉冲，则可以写出ZOH的传递函数：

根据传递函数，可以分析ZOH的幅频、相频特性：

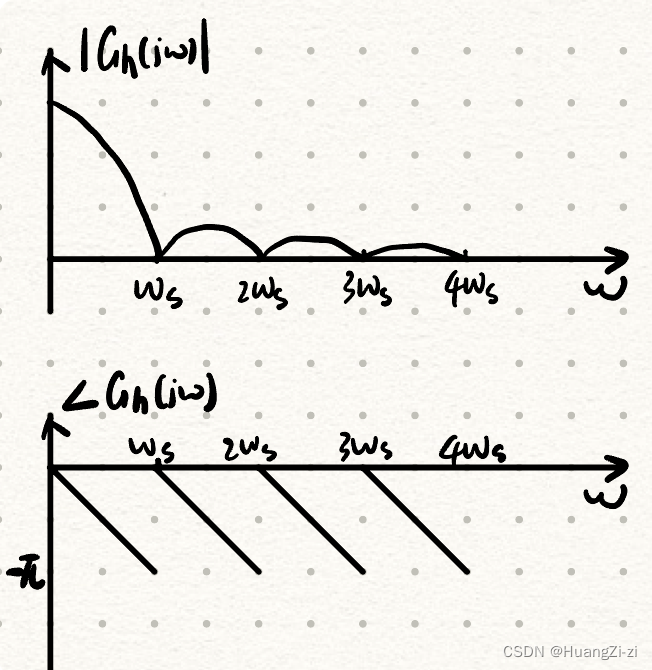
1. 有无穷多个截止频率：${\omega }_c=n{\omega }_s$
2. 允许高频分量通过，但幅值随$\omega$增加而衰减
3. 相位滞后。滞后程度与信号频率$\omega$及采样周期$T$成正比

零阶保持器容易实现，是应用最广泛的一种信号重构法。

一阶保持器：
$f(t)=f(kT+\Delta t)=a_0+a_1\Delta t$
了解即可。

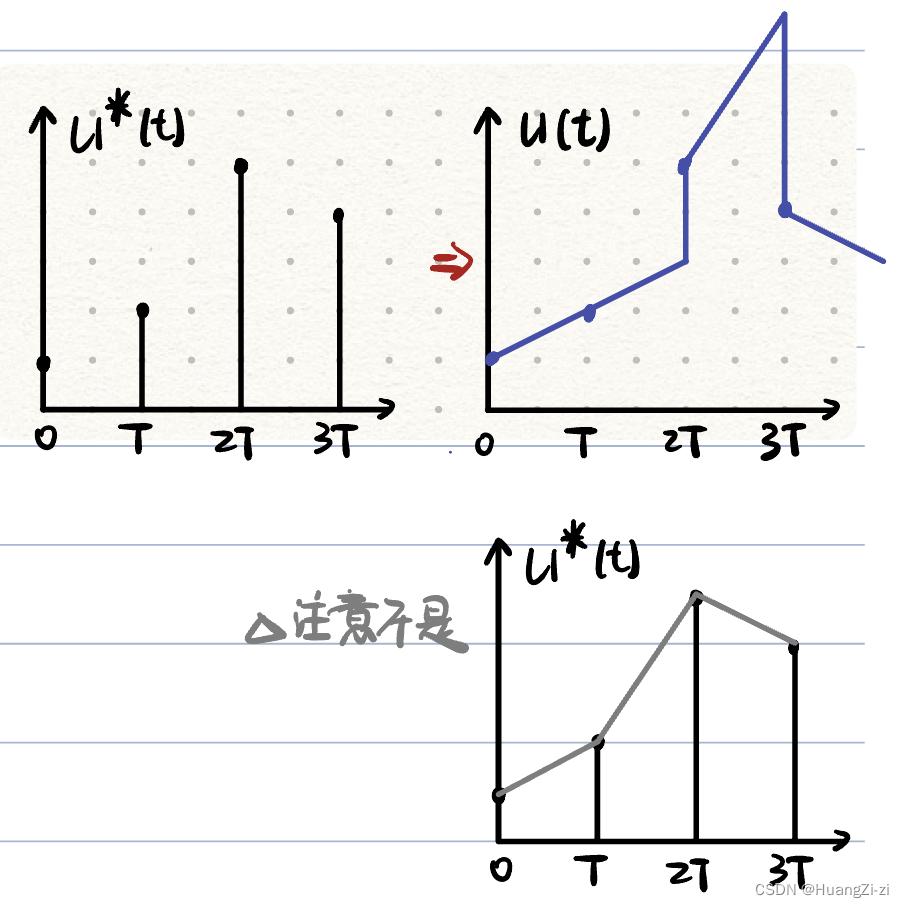
这里需要注意的是，斜率必须根据kT之前的采样值计算，而不能直接连接kT和(k+1)T的采样值。