拦截导弹

题目链接:acwing1010. 拦截导弹
题目描述：

输入输出:

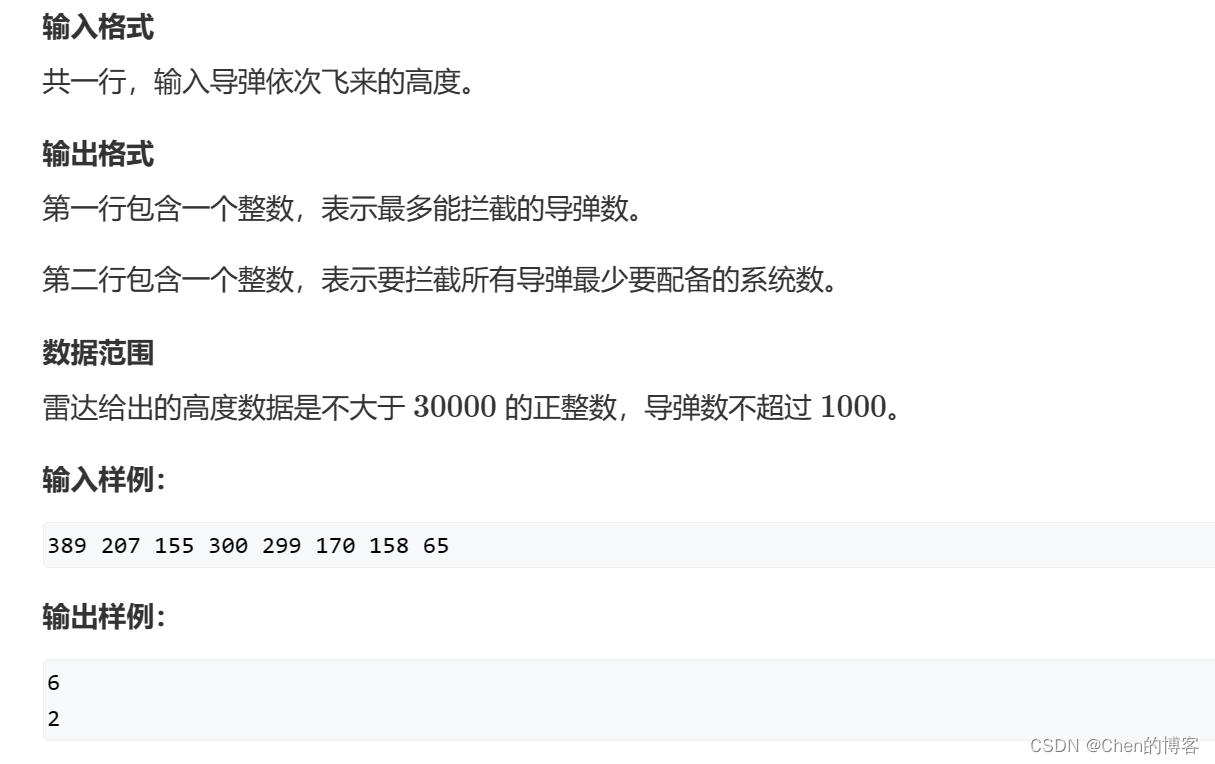
分析：
第一个问题为输出最长递减子序列，由于导弹数在1000以内所以采用时间复杂度为$O(n^2)$或者$O(nlogn)$的算法都可以。
第二个问题，可以用贪心的思想来做，每次新到的导弹，我们用当前导弹高度恰好大于等于该导弹高度的导弹系统去拦截，这样所用的导弹系统的数量是最少的。

我这里求最长上升子序列和贪心的时间复杂度都为$O(nlogn)$
** 代码如下：**

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
using namespace std;
const int N=1100;

int f[N];
int p[N];
int q[N];
int binary_search(int l,int r,int x){
    int mid;
    while(l<r){
        int mid=l+r>>1;
        if(p[mid]>=x) r=mid;
        else l=mid+1;
    }
    return r;
}
int binary_search_len(int l,int r,int x){
    int mid;
    while(l<r){
        int mid=l+r>>1;
        if(q[mid]>x) r=mid;
        else l=mid+1;
    }
    return r;
}
int main(){
    int n=0;
    while(scanf("%d",&f[n+1])!=EOF) n++;
    int k=0;
    for(int i=n;i>=1;i--){
        if(k==0||f[i]>=q[k]) q[++k]=f[i];
        else{
            int t=binary_search_len(1,k,f[i]);
            q[t]=f[i];
        }
    }
    printf("%d\n",k);
    
    k=0;
    for(int i=1;i<=n;i++){
        if(!k||p[k]<f[i]) p[++k]=f[i];
        else{
            int t=binary_search(1,k,f[i]);
            p[t]=f[i];
        }
    }
    printf("%d\n",k);
    return 0;
}

导弹防御系统

题目链接:acwing1010. 导弹防御系统
题目描述：

输入输出:

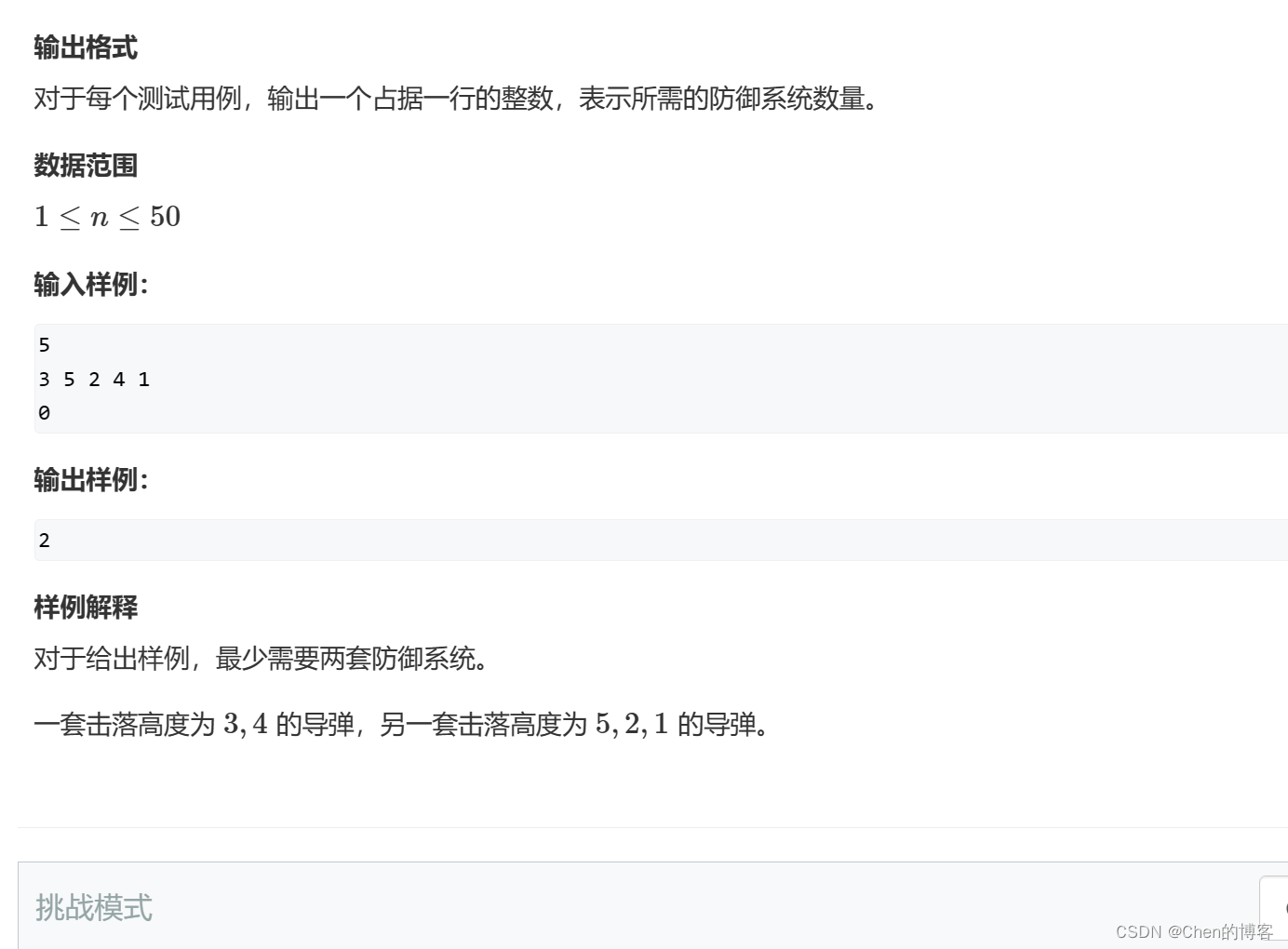
**分析：**这道题稍微复杂一些，因为有两种拦截导弹的可能，由于数据范围较小，可以直接暴力枚举每一种可能，$dfs+剪枝$就行。
代码如下：

/*dfs+剪枝*/
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=55;

int n,f[N];
int up[N],down[N];
int ans;
void dfs(int u,int p,int d){//分别表示递归到哪个元素,up元素个数,down的元素个数
    if(p+d>=ans) return;//剪枝
    if(u==n){
        ans=p+d;
        return;
    }
    //down
    int k=0;
    while(k<p&&up[k]<=f[u]) k++;
    int t=up[k];
    up[k]=f[u];
    if(k<p) dfs(u+1,p,d);
    else dfs(u+1,p+1,d);
    up[k]=t;
    //up
    k=0;
    while(k<d&&down[k]>=f[u]) k++;
    t=down[k];
    down[k]=f[u];
    if(k<d) dfs(u+1,p,d);
    else dfs(u+1,p,d+1);
    down[k]=t;
}
int main(){
    
    while(cin>>n,n){
        for(int i=0;i<n;i++) scanf("%d",&f[i]);
        ans=n;
        dfs(0,0,0);
        cout<<ans<<endl;
    }
    return 0;
}