[NOIP2008 普及组] 立体图
题目描述
小渊是个聪明的孩子,他经常会给周围的小朋友们讲些自己认为有趣的内容。最近,他准备给小朋友们讲解立体图,请你帮他画出立体图。
小渊有一块面积为 m × n m \times n m×n 的矩形区域,上面有 m × n m \times n m×n 个边长为 1 1 1 的格子,每个格子上堆了一些同样大小的积木(积木的长宽高都是 1 1 1),小渊想请你打印出这些格子的立体图。我们定义每个积木为如下格式,并且不会做任何翻转旋转,只会严格以这一种形式摆放:
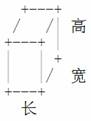
每个顶点用
1
1
1 个加号 + 表示,长用
3
3
3 个 - 表示,宽用
1
1
1 个 /,高用两个 | 表示。字符 +,-,/,| 的 ASCII 码分别为
43
43
43,
45
45
45,
47
47
47,
124
124
124。字符 .(ASCII 码
46
46
46)需要作为背景输出,即立体图里的空白部分需要用 . 来代替。立体图的画法如下面的规则:
若两块积木左右相邻,图示为:
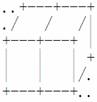
若两块积木上下相邻,图示为:
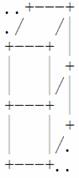
若两块积木前后相邻,图示为:

立体图中,定义位于第 ( m , 1 ) (m,1) (m,1) 的格子(即第 m m m 行第 1 1 1 列的格子)上面自底向上的第一块积木(即最下面的一块积木)的左下角顶点为整张图最左下角的点。
输入格式
第一行有用空格隔开的 2 2 2个整数 m m m 和 n n n,表示有 m × n m \times n m×n 个格子 ( 1 ≤ m , n ≤ 50 ) (1 \le m,n \le 50) (1≤m,n≤50)。
接下来的 m m m 行,是一个 m × n m \times n m×n 的矩阵,每行有 n n n 个用空格隔开的整数,其中第 i i i 行第 j j j 列上的整数表示第 i i i 行第 j j j 列的格子上摞有多少个积木($1 \le $ 每个格子上的积木数 $ \le 100$)。
输出格式
输出包含题目要求的立体图,是一个 K K K 行 L L L 列的字符串矩阵,其中 K K K 和 L L L 表示最少需要 K K K 行 L L L 列才能按规定输出立体图。
样例 #1
样例输入 #1
3 4
2 2 1 2
2 2 1 1
3 2 1 2
样例输出 #1
......+---+---+...+---+
..+---+ / /|../ /|
./ /|-+---+ |.+---+ |
+---+ |/ /| +-| | +
| | +---+ |/+---+ |/|
| |/ /| +/ /|-+ |
+---+---+ |/+---+ |/| +
| | | +-| | + |/.
| | |/ | |/| +..
+---+---+---+---+ |/...
| | | | | +....
| | | | |/.....
+---+---+---+---+......
提示
NOIP2008普及组第四题
#include<bits/stdc++.h>
using namespace std;
//
int h[101][101];
int z[6]={2,1,0,0,0,0},s[6]={6,6,6,6,5,4};
int maxx=0,maxy=0;
char c[1001][1001];
char cube[10][10]={
" +---+",
" / /|",
"+---+ |",
"| | +",
"| |/",
"+---+",
};
//
void draw(int x,int y){
for(int i=5; i>=0; i--){
for(int j=z[i]; j<=s[i]; j++){
c[5-i+x][y+j]=cube[i][j];
if(5-i+x>maxx) maxx=5-i+x;
if(j+y>maxy) maxy=j+y;
}
}
}
//
int main(){
int m,n; cin>>m>>n;
for(int i=1; i<=m; i++)
for(int j=0; j<n; j++)
cin>>h[i][j];
//
for(int i=1; i<=m; i++){
for(int j=0; j<n; j++){
for(int k=0; k<h[i][j]; k++){
draw( (m-i)*2+1+3*k , (m-i)*2+1+4*j);
}
}
}
//
for(int i=maxx; i>=1; i--){
for(int j=1; j<=maxy; j++)
if( c[i][j]==0 ) cout<<".";
else cout<<c[i][j];
cout<<endl;
}
return 0;
}