一、说明
在图型学中,欧拉公式很有用处,比如皮克定律也可以用欧拉公式证明。本篇介绍欧拉公式的定义和三个证明过程。
二、欧拉公式
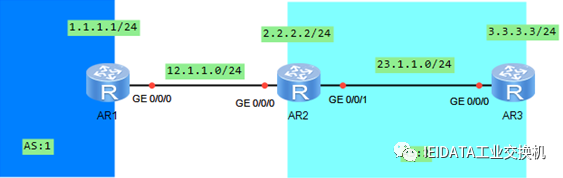
在任何一个规则球面地图上,用 R记区域个 数 ,V记顶点个数 ,E记边界个数 ,则 R+ V- E= 2,这就是欧拉定理 ,它于 1640年由 Descartes(笛卡尔)首先给出证明 。
后来 Euler(欧拉 )于 1752年又独立地给出证明 ,我们称其为欧拉定理 ,在国外也有人称其 为 Descartes定理。
R+ V- E= 2 就是欧拉公式。
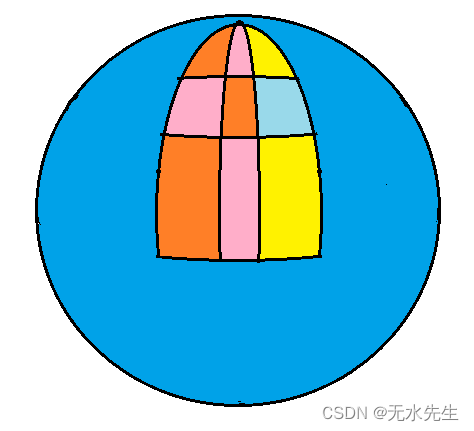
如上图: R =10 ,V = 13 ,E = 21,因此,R+ V- E= 2成立。
三、欧拉的证明
3.1 当R=2时候
( 1) 当 R= 2时 ,由说明 1,这两个区域可想象为 以赤道为边界的两个半球面 ,赤道上有两个“顶点” 将赤道分成两条“边界”,即 R= 2,V= 2,E= 2;于是 R+ V- E= 2,欧拉定理成立。
3.2 当R大于2时
( 2) 设 R= m(m≥ 2)时欧拉定理成立 ,下面证明 R= m+ 1时欧拉定理也成立 。
我们在 R= m+ 1的地图上任选一个 区域 X ,则 X 必有与它如此相邻的区域 Y ,使得在 去掉 X 和 Y 之间的唯一一条边界后 ,地图上只有 m 个区域了;在去掉 X 和 Y 之间的边界后 ,若原该边界两端 的顶点现在都还是 3条或 3条以上边界的顶点 ,则 该顶点保留 ,同时其他的边界数不变;若原该边界一 端或两端的顶点现在成为 2条边界的顶点 ,则去掉 该顶点 ,该顶点两边的两条边界便成为一条边界 。
于是 ,在去掉 X 和 Y之间的唯一 一条边界时只有三种情况:
- ①减少一个区域,同时减少一条边界;
- ②减少一个区域、同时减少一个顶点和两条边界;
- ③减少一个区域,同时减少两个顶点和三条边界;
以上情况如下图说明:
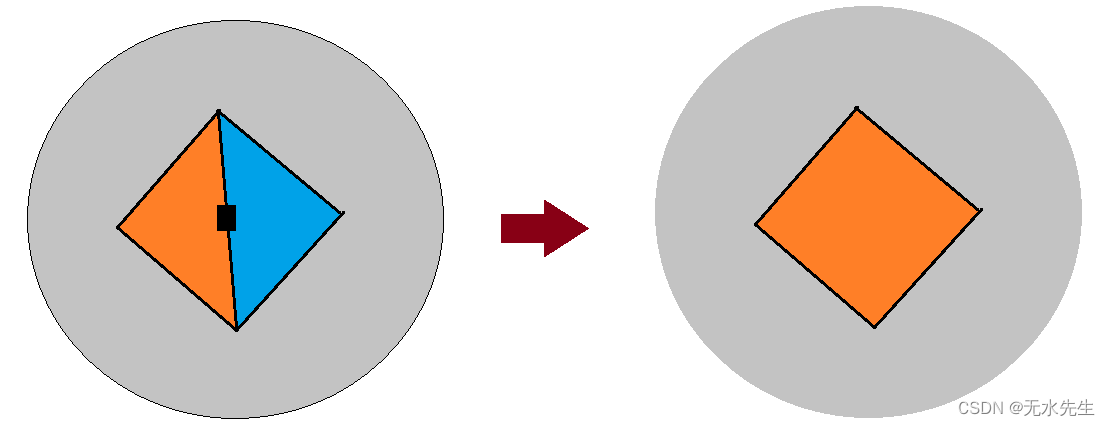
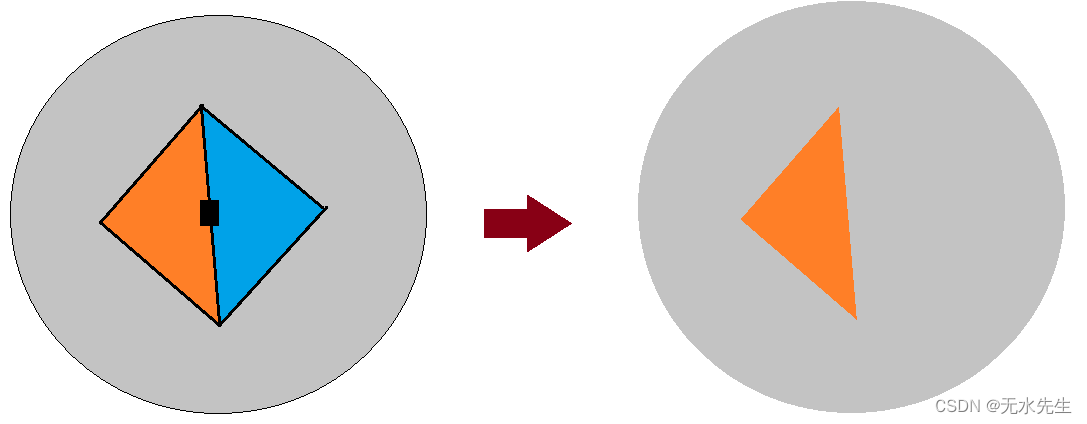
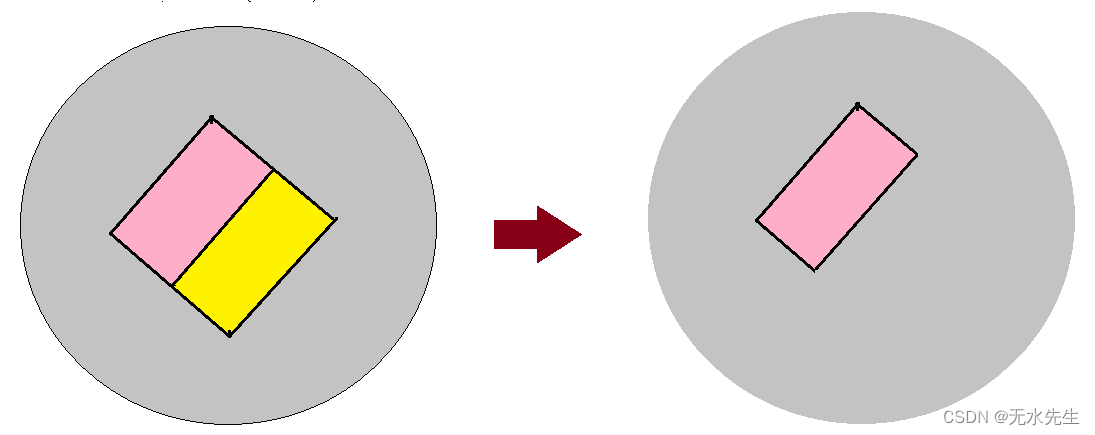
即在去掉 X 和 Y 之间的边界时 ,不 论何种情况都必定有“减少的区域数 + 减少的顶点数 = 减少的边界数”.
| 减少区域数Rsub | 减少边界Esub | 减少顶点Vsub | 平恒公式 |
|---|---|---|---|
| 1 | 1 | 0 | Rsub +Vsub - Esub =0 |
| 1 | 2 | 1 | |
| 1 | 3 | 2 |
我们将上述过程反过来 (即将 X 和 Y之间去掉的边 界又照原样画上 ) ,就又成为 R= m+ 1的地图了 ,在 这一过程中必然是“增加的区域数 + 增加的顶点数 = 增加的边界数”。
因此 ,若 R= m (m≥2)时欧拉定理成立 ,则 R= m+ 1时欧拉定理也成立.。
由 ( 1)和 ( 2)可知 ,对于任何正整数 R≥2,欧拉 定理成立。
四、柯西的证明
第一个欧拉公式的严格证明,由20岁的 柯西给出,大致如下:
欧拉公式
从多面体去掉一面,通过把去掉的面的边互相拉远,把所有剩下的面变成点和曲线的平面网络。不失一般性,可以假设变形的边继续保持为直线段。正常的面不再是正常的多边形即使开始的时候它们是正常的。但是,点,边和面的个数保持不变,和给定多面体的一样(移去的面对应网络的外部。)
重复一系列可以简化网络却不改变其欧拉数(也是欧拉示性数)
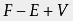
的额外变换。
-
若有一个多边形面有3条边以上,我们划一个对角线。这增加一条边和一个面。继续增加边直到所有面都是三角形。
-
除掉只有一条边和外部相邻的三角形。这把边和面的个数各减一而保持顶点数不变。
-
(逐个)除去所有和网络外部共享两条边的三角形。这会减少一个顶点、两条边和一个面。
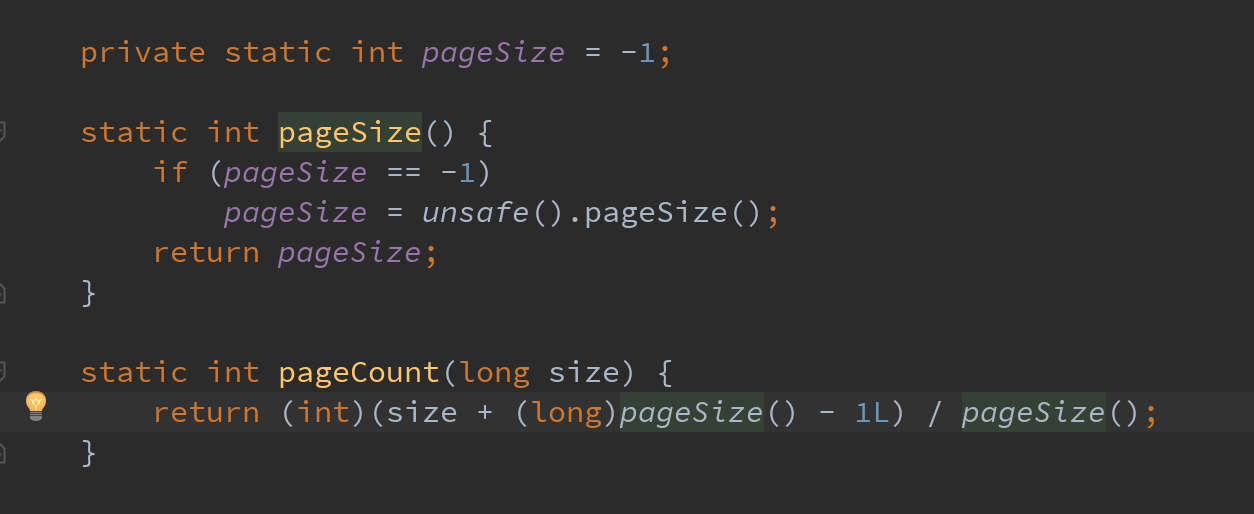
重复使用第2步和第3步直到只剩一个三角形。对于一个三角形
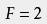
(把外部数在内),。所以。
五、推理证明
设想这个多面体是先有一个面,然后将其他各面一个接一个地添装上去的.因为一共有F个面,因此要添(F-1)个面.
考察第Ⅰ个面,设它是n边形,有n个顶点,n条边,这时E=V,即棱数等于顶点数.
添上第Ⅱ个面后,因为一条棱与原来的棱重合,而且有两个顶点和第Ⅰ个面的两个顶点重合,所以增加的棱数比增加的顶点数多1,因此,这时E=V+1.
以后每增添一个面,总是增加的棱数比增加的顶点数多1,例如
增添两个面后,有关系E=V+2;
增添三个面后,有关系E=V+3;
……
增添(F-2)个面后,有关系E=V+ (F-2).
最后增添一个面后,就成为多面体,这时棱数和顶点数都没有增加.因此,关系式仍为E=V+ (F-2).即
F+V=E+2.
这个公式叫做欧拉公式.它表明2这个数是简单多面体表面在连续变形下不变的数。