对比斐波那契和快排时间复杂度

news2024/11/27 21:00:51

斐波那契数列时间复杂度

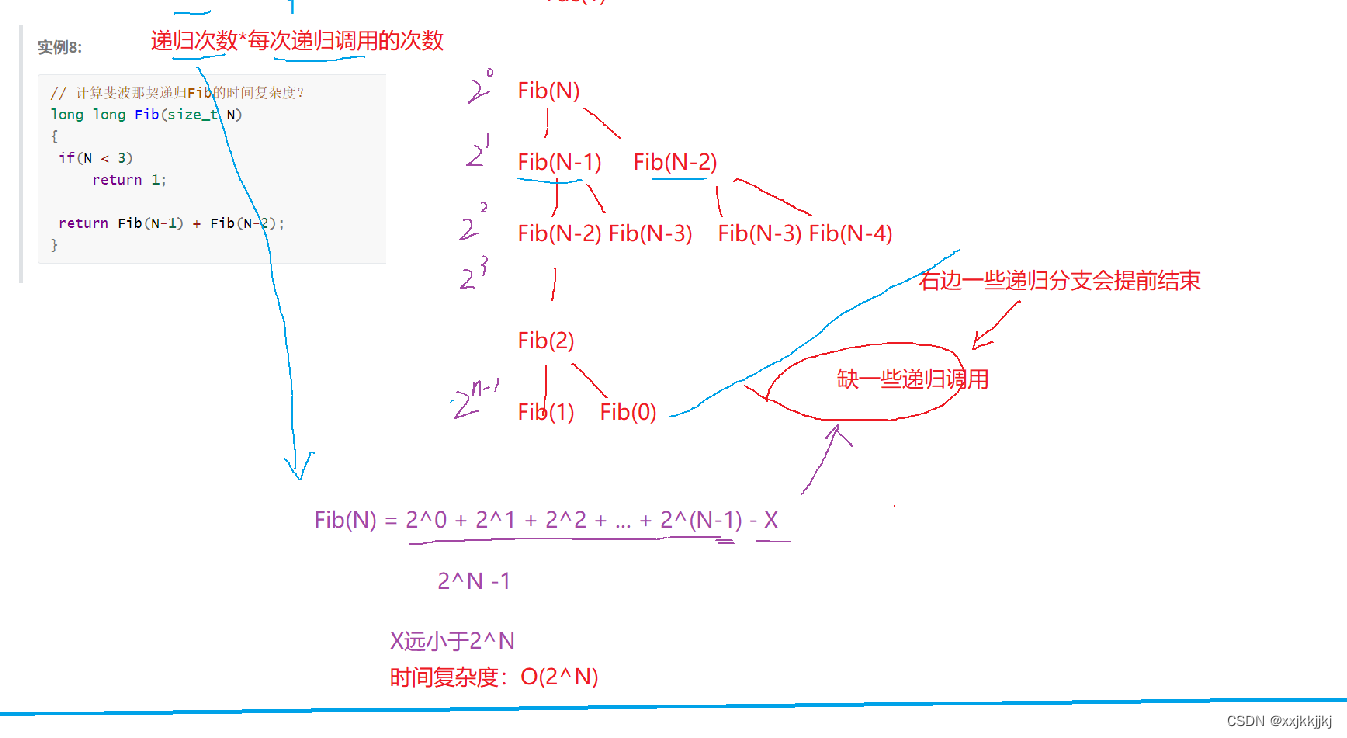
在这里插入图片描述

// 计算斐波那契递归Fib的时间复杂度？
long long Fib(size_t N)
{
 if(N < 3)
 return 1;
 
 return Fib(N-1) + Fib(N-2);
}

Fib()递归高度是N，那它最后一层就是2^(N-1)
如果N=50，最后一层是2^(49)=一个恐怖的值

更恐怖的是还是一个等差数列，最后算出时间复杂度O(2^n)

假设你有N=10亿数据
你只需要h = logN = 30层
这里10亿数据只需要30层
每一层大概是N 一共有高度层logN
时间复杂度是O(NlogN)
排好

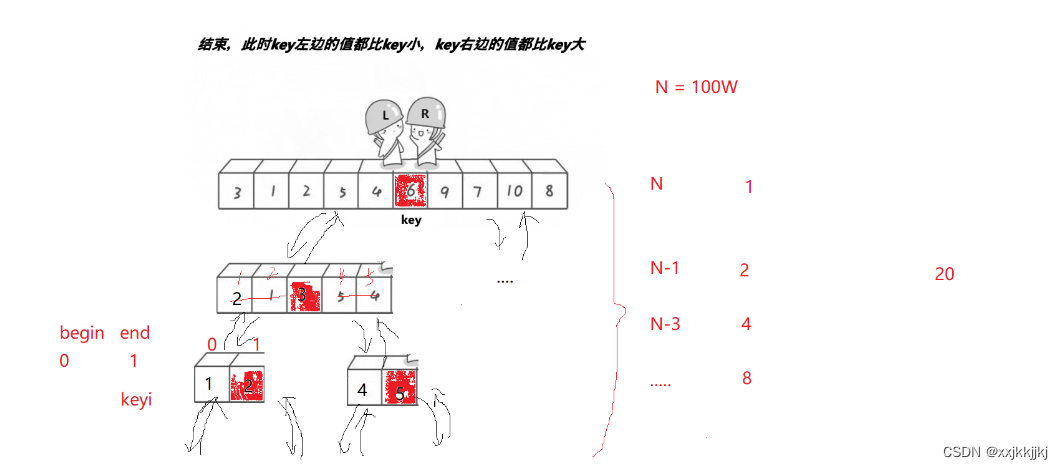
在这里插入图片描述
Fib是你有N=10亿你就要递归10亿层，二叉树右边会缺一些但还是很多节点，所以很慢，主要原因是二叉树的高度太高
快排是我有h=logN层数据高度不高也能存很多数据，每层我排N次大概，就能排好

N = 10亿

NlogN = 10亿*30 = 300亿

2^n = 2^10亿 = 恐怖的一个值

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/423499.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！