传球游戏

题目描述

​ 上体育课的时候，小蛮的老师经常带着同学们一起做游戏。这次，老师带着同学们一起做传球游戏。
​ 游戏规则是这样的：n个同学站成一个圆圈，其中的一个同学手里拿着一个球，当老师吹哨子时开始传球，每个同学可以把球传给自己左右的两个同学中的一个（左右任意），当老师再次吹哨子时，传球停止，此时，拿着球没传出去的那个同学就是败者，要给大家表演一个节目。
​ 聪明的小蛮提出一个有趣的问题：有多少种不同的传球方法可以使得从小蛮手里开始传的球，传了m次以后，又回到小蛮手里。两种传球的方法被视作不同的方法，当且仅当这两种方法中，接到球的同学按接球顺序组成的序列是不同的。比如有3个同学1号、2号、3号，并假设小蛮为1号，球传了3次回到小蛮手里的方式有1->2->3->1和1->3->2->1，共2种。

输入描述

共一行，有两个用空格隔开的整数n，m（ 3 ≤ n ≤ 30，1 ≤ m ≤ 30 ）。

输出描述

共一行，有一个整数，表示符合题意的方法数。

样例

3 3

2

提示

• 40%的数据满足：3 ≤ n ≤ 30，1 ≤ m ≤ 20
• 100%的数据满足：3 ≤ n ≤ 30，1 ≤ m ≤ 30。
• https://ac.nowcoder.com/acm/problem/16619

分析

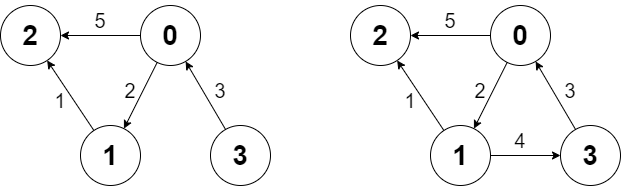
看题目给出的样例，1->2->3->1 和 1->3->2->1，共2种。

首先从最后思考，可以看到从 1 开始传球，最后回到 1，那么它是如何回到这个 1 的呢？也就是说，它的上一个拿着球的人是谁呢（因为要从这个人传给 1）？

• 有两个方向，一个是 1 的左边或 1 的右边，即为 n 或 2

那么 n 的球源又来着哪里呢？

• 同样的，一个是 n 的左边或 n 的右边，即为 n-1 或 1

由上述可知，本题具有“重叠子问题” 可用 DP 解决。
现在我们知道：1 的左边是 n，右边是 2，而 n 的左边是 n-1，右边是 1，2 的左边和右边同理…
由此可见：第 i 次传球，想要球若在 j 手里，则必须第 i-1 次传球，球若在 j-1 或 j+1 手里。
Tips：当 j = 1 或 j = n 时，需要额外考虑。

• 原问题：从 1 开始传球，最后回到 1 的方案数
• 子问题：第 i 次传球，球若在 j 手里的方案数
• DP 定义：第 i 次传球，球若在 j 手里的方案数
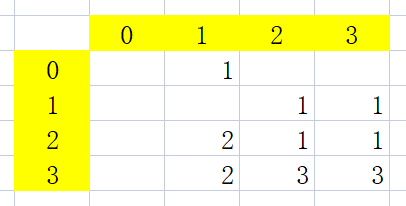
• DP 方程：
  • 正常情况 ：$dp[i][j]=dp[i-1][j-1]+dp[i-1][j+1]$
  • 当 j = 1 时：$dp[i][j]=dp[i-1][n]+dp[i-1][j+1]$
  • 当 j = n 时：$dp[i][j]=dp[i-1][j-1]+dp[i-1][1]$
• DP 初始化：$dp[0][1]=1$（第 0 次传球，球落在 1 手里的方案数）

代码

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt(), m = sc.nextInt();
        int MAX = 35;
        int[][] dp = new int[MAX][MAX];
        dp[0][1] = 1;
        for(int i = 1; i <= m; i++) {
            dp[i][1] = dp[i-1][n] + dp[i-1][1+1];
            for(int j = 2; j < n; j++) {
                dp[i][j] = dp[i-1][j+1] + dp[i-1][j-1];
            }
            dp[i][n] = dp[i-1][n-1] + dp[i-1][1];
        }
        
        System.out.println(dp[m][1]);
    }
}

草稿纸