文章目录

双周赛102
- [6333. 查询网格图中每一列的宽度](https://leetcode.cn/problems/find-the-width-of-columns-of-a-grid/)
- - 模拟
- [6334. 一个数组所有前缀的分数](https://leetcode.cn/problems/find-the-score-of-all-prefixes-of-an-array/)
- - 模拟(一次遍历)
- 😭[6335. 二叉树的堂兄弟节点 II](https://leetcode.cn/problems/cousins-in-binary-tree-ii/)
- - BFS遍历
- [6336. 设计可以求最短路径的图类](https://leetcode.cn/problems/design-graph-with-shortest-path-calculator/)
- - 求最短路模板题
  - - Dijkstra
    - Floyd算法

双周赛102

6333. 查询网格图中每一列的宽度

难度简单2

给你一个下标从 0 开始的 m x n 整数矩阵 grid 。矩阵中某一列的宽度是这一列数字的最大 字符串长度 。

比方说，如果 grid = [[-10], [3], [12]] ，那么唯一一列的宽度是 3 ，因为 -10 的字符串长度为 3 。

请你返回一个大小为 n 的整数数组 ans ，其中 ans[i] 是第 i 列的宽度。

一个有 len 个数位的整数 x ，如果是非负数，那么 字符串****长度 为 len ，否则为 len + 1 。

示例 1：

输入：grid = [[1],[22],[333]]
输出：[3]
解释：第 0 列中，333 字符串长度为 3 。

示例 2：

输入：grid = [[-15,1,3],[15,7,12],[5,6,-2]]
输出：[3,1,2]
解释：
第 0 列中，只有 -15 字符串长度为 3 。
第 1 列中，所有整数的字符串长度都是 1 。
第 2 列中，12 和 -2 的字符串长度都为 2 。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 100
-109 <= grid[r][c] <= 109

模拟

class Solution {
    public int[] findColumnWidth(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int[] res = new int[n];
        for(int i = 0; i < n; i++){
            int max = 0;
            for(int j = 0; j < m; j++){
                max = Math.max(max,String.valueOf(grid[j][i]).length());
            }
            res[i] = max;
        }
        return res;
    }
}

6334. 一个数组所有前缀的分数

难度中等0

定义一个数组 arr 的 转换数组 conver 为：

conver[i] = arr[i] + max(arr[0..i])，其中 max(arr[0..i]) 是满足 0 <= j <= i 的所有 arr[j] 中的最大值。

定义一个数组 arr 的分数为 arr 转换数组中所有元素的和。

给你一个下标从 0 开始长度为 n 的整数数组 nums ，请你返回一个长度为 n 的数组 ans ，其中 ans[i]是前缀 nums[0..i] 的分数。

示例 1：

输入：nums = [2,3,7,5,10]
输出：[4,10,24,36,56]
解释：
对于前缀 [2] ，转换数组为 [4] ，所以分数为 4 。
对于前缀 [2, 3] ，转换数组为 [4, 6] ，所以分数为 10 。
对于前缀 [2, 3, 7] ，转换数组为 [4, 6, 14] ，所以分数为 24 。
对于前缀 [2, 3, 7, 5] ，转换数组为 [4, 6, 14, 12] ，所以分数为 36 。
对于前缀 [2, 3, 7, 5, 10] ，转换数组为 [4, 6, 14, 12, 20] ，所以分数为 56 。

示例 2：

输入：nums = [1,1,2,4,8,16]
输出：[2,4,8,16,32,64]
解释：
对于前缀 [1] ，转换数组为 [2] ，所以分数为 2 。
对于前缀 [1, 1]，转换数组为 [2, 2] ，所以分数为 4 。
对于前缀 [1, 1, 2]，转换数组为 [2, 2, 4] ，所以分数为 8 。
对于前缀 [1, 1, 2, 4]，转换数组为 [2, 2, 4, 8] ，所以分数为 16 。
对于前缀 [1, 1, 2, 4, 8]，转换数组为 [2, 2, 4, 8, 16] ，所以分数为 32 。
对于前缀 [1, 1, 2, 4, 8, 16]，转换数组为 [2, 2, 4, 8, 16, 32] ，所以分数为 64 。

提示：

1 <= nums.length <= 105
1 <= nums[i] <= 109

模拟(一次遍历)

class Solution {
    public long[] findPrefixScore(int[] nums) {
        int n = nums.length;
        long[] res = new long[n];
        int max = nums[0];
        long sum = 0l;
        for(int i = 0; i < n; i++){
            max = Math.max(max, nums[i]); // 维护前缀最大值
            sum += (long)nums[i] + (long)max;
            res[i] = sum;
        }
        return res;
    }
}

😭6335. 二叉树的堂兄弟节点 II

难度中等0

给你一棵二叉树的根 root ，请你将每个节点的值替换成该节点的所有 堂兄弟节点值的和 。

如果两个节点在树中有相同的深度且它们的父节点不同，那么它们互为 堂兄弟 。

请你返回修改值之后，树的根 root 。

注意，一个节点的深度指的是从树根节点到这个节点经过的边数。

示例 1：

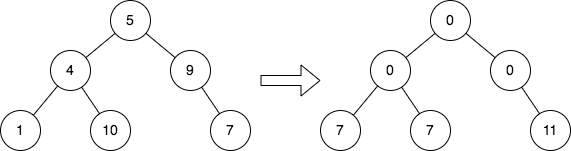
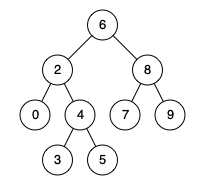
输入：root = [5,4,9,1,10,null,7]
输出：[0,0,0,7,7,null,11]
解释：上图展示了初始的二叉树和修改每个节点的值之后的二叉树。
- 值为 5 的节点没有堂兄弟，所以值修改为 0 。
- 值为 4 的节点没有堂兄弟，所以值修改为 0 。
- 值为 9 的节点没有堂兄弟，所以值修改为 0 。
- 值为 1 的节点有一个堂兄弟，值为 7 ，所以值修改为 7 。
- 值为 10 的节点有一个堂兄弟，值为 7 ，所以值修改为 7 。
- 值为 7 的节点有两个堂兄弟，值分别为 1 和 10 ，所以值修改为 11 。

示例 2：

输入：root = [3,1,2]
输出：[0,0,0]
解释：上图展示了初始的二叉树和修改每个节点的值之后的二叉树。
- 值为 3 的节点没有堂兄弟，所以值修改为 0 。
- 值为 1 的节点没有堂兄弟，所以值修改为 0 。
- 值为 2 的节点没有堂兄弟，所以值修改为 0 。

提示：

树中节点数目的范围是 [1, 105] 。
1 <= Node.val <= 104

BFS遍历

https://leetcode.cn/problems/cousins-in-binary-tree-ii/solution/bfssuan-liang-ci-pythonjavacgo-by-endles-b72a/

站在父节点的视角，去看下一层节点的取值：（站在父节点的位置上解决子节点的问题）！！！启发点：对于一个节点 x 来说，它的所有堂兄弟节点值的和，等价于 x 这层的所有节点值之和，减去 x 及其兄弟节点的值之和

BFS层序遍历二叉树，对于每一层：

首先，遍历当前层的每个节点，通过节点的左右儿子，计算下层的节点值之和 nextLevelSum;

然后，再次遍历当前层的每个节点 x，计算 x 的左右儿子的节点值之和 childrenSum，更新 x 的左右儿子的节点值为nextLevelSum - childrenSum。

class Solution {
    public TreeNode replaceValueInTree(TreeNode root) {
        root.val = 0;
        // 使用List和临时变量tmp来模拟队列（Deque没有get方法）
        List<TreeNode> q = new ArrayList<>();
        q.add(root);
        while(!q.isEmpty()){
            // 用临时遍历保存本层节点，后面需要计算本层节点x左右儿子的节点值之和
            List<TreeNode> tmp = q;
            q = new ArrayList<>();
            int nextLevelSum = 0; // 下一层的节点之和
            // 获取下层节点和的同时进行BFS操作
            for(TreeNode node : tmp){
                if(node.left != null){
                    q.add(node.left);
                    nextLevelSum += node.left.val;
                }
                if(node.right != null){
                    q.add(node.right);
                    nextLevelSum += node.right.val;
                }
            }
            // 再次遍历，更新下一层的节点值
            for(TreeNode node : tmp){
                int childSum = (node.left != null ? node.left.val : 0) + 
                                (node.right != null ? node.right.val : 0);
                if(node.left != null) node.left.val = nextLevelSum - childSum;
                if(node.right != null) node.right.val = nextLevelSum - childSum;
            }
        }
        return root;
    }
}

6336. 设计可以求最短路径的图类

难度困难0

给你一个有 n 个节点的 有向带权 图，节点编号为 0 到 n - 1 。图中的初始边用数组 edges 表示，其中 edges[i] = [fromi, toi, edgeCosti] 表示从 fromi 到 toi 有一条代价为 edgeCosti 的边。

请你实现一个 Graph 类：

Graph(int n, int[][] edges) 初始化图有 n 个节点，并输入初始边。
addEdge(int[] edge) 向边集中添加一条边，其中 edge = [from, to, edgeCost] 。数据保证添加这条边之前对应的两个节点之间没有有向边。
int shortestPath(int node1, int node2) 返回从节点 node1 到 node2 的路径最小代价。如果路径不存在，返回 -1 。一条路径的代价是路径中所有边代价之和。

示例 1：

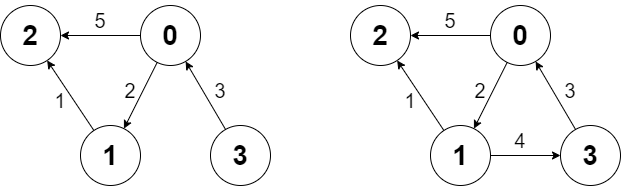
输入：
["Graph", "shortestPath", "shortestPath", "addEdge", "shortestPath"]
[[4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]], [3, 2], [0, 3], [[1, 3, 4]], [0, 3]]
输出：
[null, 6, -1, null, 6]

解释：
Graph g = new Graph(4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]);
g.shortestPath(3, 2); // 返回 6 。从 3 到 2 的最短路径如第一幅图所示：3 -> 0 -> 1 -> 2 ，总代价为 3 + 2 + 1 = 6 。
g.shortestPath(0, 3); // 返回 -1 。没有从 0 到 3 的路径。
g.addEdge([1, 3, 4]); // 添加一条节点 1 到节点 3 的边，得到第二幅图。
g.shortestPath(0, 3); // 返回 6 。从 0 到 3 的最短路径为 0 -> 1 -> 3 ，总代价为 2 + 4 = 6 。

提示：

1 <= n <= 100
0 <= edges.length <= n * (n - 1)
edges[i].length == edge.length == 3
0 <= fromi, toi, from, to, node1, node2 <= n - 1
1 <= edgeCosti, edgeCost <= 106
图中任何时候都不会有重边和自环。
调用 addEdge 至多 100 次。
调用 shortestPat
h 至多 100 次。

求最短路模板题

Dijkstra

Dijkstra模板：https://blog.csdn.net/qq_42958831/article/details/129637869

class Graph {

    private static final int INF = Integer.MAX_VALUE / 2;
    int n;
    int[][] g;
    
    public Graph(int n, int[][] edges) {
        this.n = n;
        g = new int[n][n];
        for(int i = 0; i < n; i++) Arrays.fill(g[i], INF);
        for(int[] e : edges){
            int from = e[0], to = e[1], cost = e[2];
            g[from][to] = cost;
        }
    }
    
    public void addEdge(int[] edge) {
        int from = edge[0], to = edge[1], cost = edge[2];
        g[from][to] = cost;
    }
    
    public int shortestPath(int node1, int node2) {
        int[] dis = new int[n];
        Arrays.fill(dis, INF);
        dis[node1] = 0;
        boolean[] used = new boolean[n];
        for(int i = 0; i < n; i++){
            int x = -1;
            for(int y = 0; y < n; y++){
                if(!used[y] && (x == -1 || dis[y] < dis[x])){
                    x = y;
                }
            }
            used[x] = true;
            for(int y = 0; y < n; y++){
                dis[y] = Math.min(dis[y], dis[x] + g[x][y]);
            }
        }
        return dis[node2] == INF ? -1 : dis[node2];
    }
}

Floyd算法

class Graph {
    /*
    Floyd定义:
    f[k][i][j] 表示除了i 和 j 之外，从 i 到 j 的路径中间点上至多为 k 的时候,从 i 到 j 的最短路的长度
    
    分类讨论：
        从 i 到 j 的最短路中间至多为 k-1 ==>
        从 i 到 j 的最短路中间至多为 k,说明 k 一定是中间节点
        f[k][i][j] = min(f[k-1][i][j], f[k-1][i][k] + f[k-1][k][j]) 
        维度优化： f[i][j] = min(f[i][j], f[i][k] + f[k][j])

        提问： 为什么维度优化，这样做还是对的？ - k表示路径中间至多为k，不包含端点

    */

    private static final int INF = Integer.MAX_VALUE / 3;
    int n;
    int[][] g;
    
    public Graph(int n, int[][] edges) {
        this.n = n;
        g = new int[n][n];
        for(int i = 0; i < n; i++){
            // 邻接矩阵（初始化为无穷大，表示 i 到 j 没有边）
            Arrays.fill(g[i], INF);
            g[i][i] = 0; // i->i 的路径初始化为0
        }
        for(int[] e : edges){
            int from = e[0], to = e[1], cost = e[2];
            g[from][to] = cost;
        }
        // Floyd维护最短路径
        for(int k = 0; k < n; k++){
            for(int i = 0; i < n; i++){
                for(int j = 0; j < n; j++){
                    g[i][j] = Math.min(g[i][j], g[i][k] + g[k][j]); 
                }
            }
        }
    }
    
    public void addEdge(int[] edge) {
        int x = edge[0], y = edge[1], cost = edge[2];
        if(cost >= g[x][y]){
            return; // 无需更新，因为目前从 x->y 最短路比新加入的点小
        }
        // 更新i->j的路径，从新加入的节点处转移
        for(int i = 0; i < n; i++){
            for(int j = 0; j < n; j++){
                //  原来： i -> j
                //  更新后： i -> x -> y -> j
                g[i][j] = Math.min(g[i][j], g[i][x] + cost + g[y][j]);
            }
        }
    }
    
    public int shortestPath(int start, int end) {
        int ans = g[start][end];
        return ans < INF/ 3 ? ans : -1; 
    }
}