单片机—定时/计数器方式产生1MHz方波
要求: 使用定时器1,采用工作方式1,在输出口P2.0产生周期未1秒的方波;
定时计数基本流程
- 计算初值
- 定义TMOD寄存器确定 T0 或 T1 为工作方式
- 把计数器初值装入 THx 和 TLx (x=0,1与上面确定的T0,T1保持一致)
- 采用中断方式时,要对 IE 和 IP 寄存器进行赋值,打开中断
- 使TRx(x=0,1) 置位, 启动定时/计数器工作
要求分析
-
定时器T1由 TH1(字节地址8DH) 和 TL1(字节地址8BH) 组成,使用时我们在其装填初值
-
T1定时器对应TMOD寄存器的高八位,采用工作方式1则对应M1M0=01,所以这里我们将TMOD的初值设为 0001 0000 转化为对应16进制数为
TMOD=0x10 -
要产生周期为1s的方波,可以利用定时器在500ms时产生溢出, 在通过软件方法是输出口P2.0的输出状态取反, 不断重复这一过程即可.
-
1s=1000ms,工作方式1是16位定时/计数器,对每一个机器周期(1μs)进行计数,其最大值为2**16=65536μs,约等于65.54ms,那么我们产生500ms的定时可以采用每次50ms的定时,并且让其计数10次来实现
-
根据公式计算初值为:
a=216 - t • fosc / 12 = 65536 - 50000 • 11.059/12 = 19456.833 (11.059MHz晶振频率)
a=216 - t • fosc / 12 = 65536 - 50000 • 12/12 = 15536 (12MHz晶振频率)
15536转化为16进制为0x3CB0 即
TH1=0x3CTL1=0xB0 -
对于查询方式来说,我们利用 TCON 定时/计数控制寄存器中 TF1的溢出来作为计数,核心思想方法同上面一致,采用每次50ms的计时,时间到产生溢出,循环溢出10次后将输出口的电平取反即可实现对应方波的.
代码编写
中断方式实现
//中断方式
#include <reg52.h> //定义头文件,我的单片机型号为80C52RC
unsigned char num; //用于循环计数变量
sbit D1=P2^0; //方波输出口为P2.0
/*中断函数 中断源:"定时/计数器1(T1)",代号3*/
void timer1() interrupt 3
{
TH1=0x3C; TL1=0xB0; //装填计数器初值
num++; //计数变量自增
}
/*程序主函数*/
void main()
{
num=0; //初始化计数变量
EA=1; //打开中断允许寄存器IE内的总开关EA
ET1=1; //打开中断允许寄存器IE内的开关ET0
TMOD=0x10; //0001 0000
//低四位,GATE=0,C/T=0,M1M0=01;选用中断源T1,方式1,16位定时器
TH1=0x3C; TL1=0xB0; //装填计数器初值
TR1=1; //启动定时器T1
while(1) // 无限循环使得方波连续
{
if(num==10) //中断函数每执行0次,取反一次,10*50ms=500ms,即led1以1s的间隔交替点亮熄灭
{
num = 0; //中断函数每执行20次,初始化计数变量
D1 = !D1; //取反
}
}
}
查询方式实现
//查询方式
#include <reg52.h> //定义头文件,我的单片机型号为80C52RC
unsigned char num; //用于循环计数变量
sbit D2=P2^1; //方波输出口为P2.1
void main()
{
num = 1; //设置计数的次数
//低四位,GATE=0,C/T=0,M1M0=01;选用定时器T1,方式1,16位定时器
TMOD = 0x10; //0001 0000
TR1 = 1; //启动T1
TH1=0x3C; TL1=0xB0; // 装载计数器初值
while(1) // 无限循环使得方波连续
{
if (TF1==1) //判断定时器T1溢出标志位是否为1
{
num++;
TF1 = 0; //清除中断
TH1=0x3C; TL1=0xB0; // 装载计数器初值
if (num==10) //若产生了10次溢出
{
2 = !D2; // 定时时间到使D2反向
num = 1;
}
}
}
}
结果演示
仿真图如下:
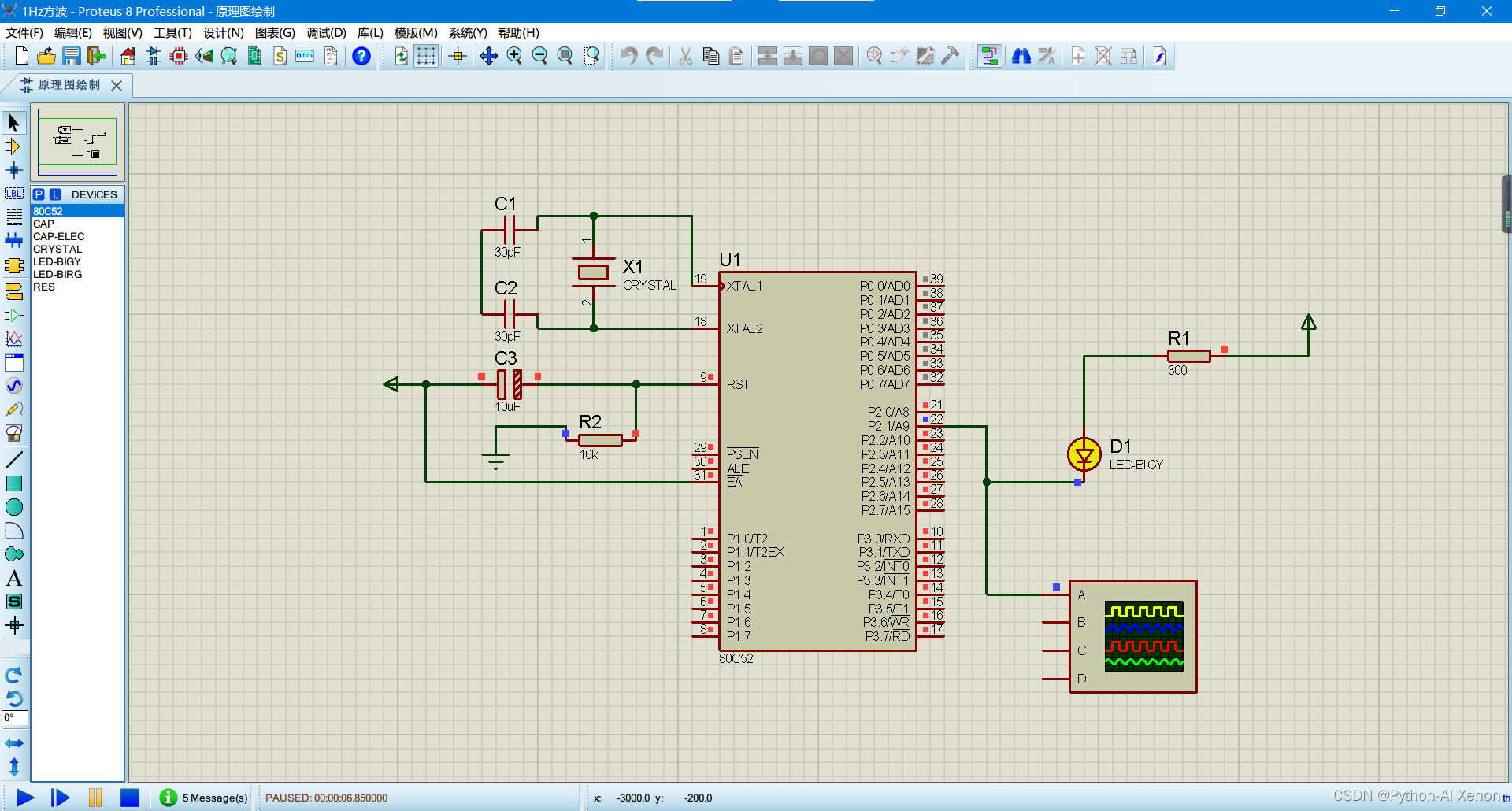
仿真效果如下:
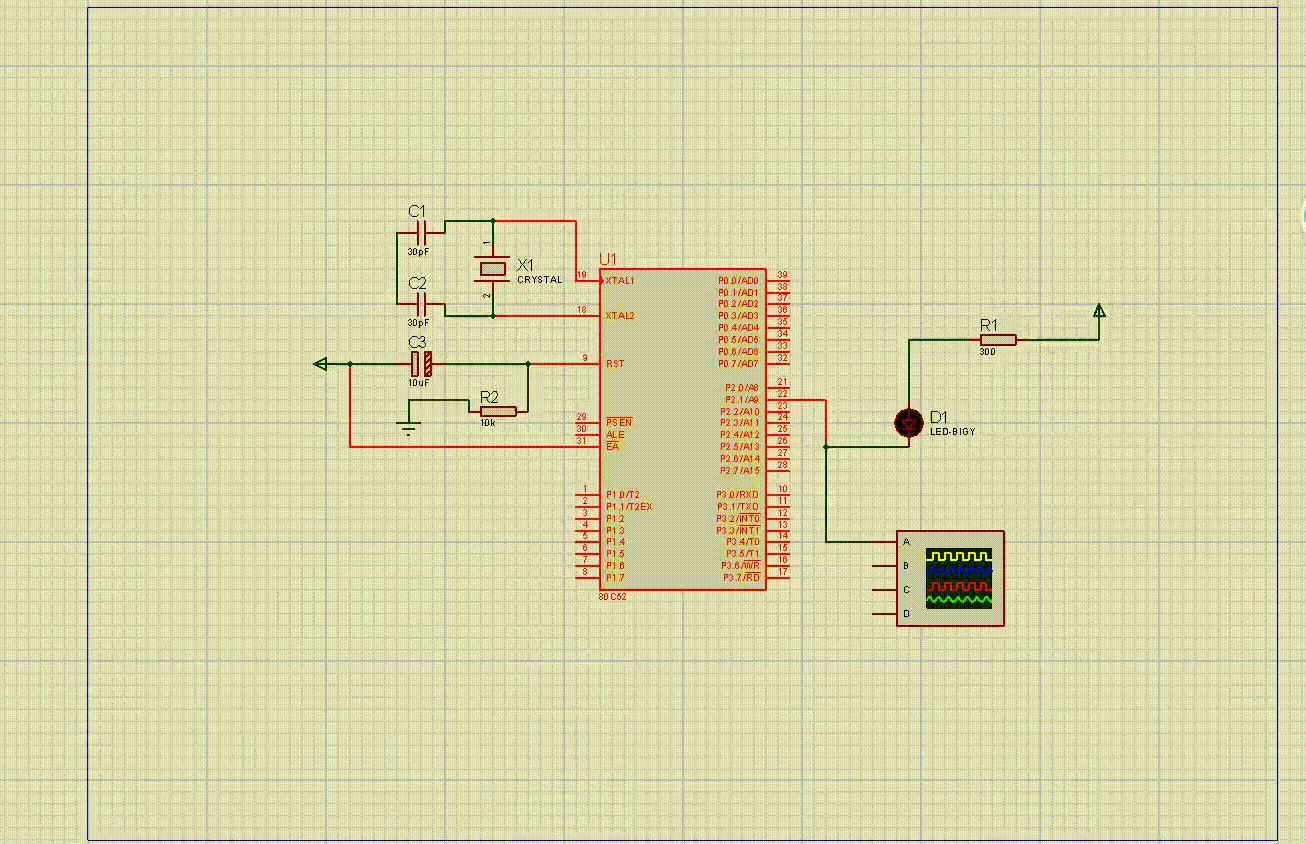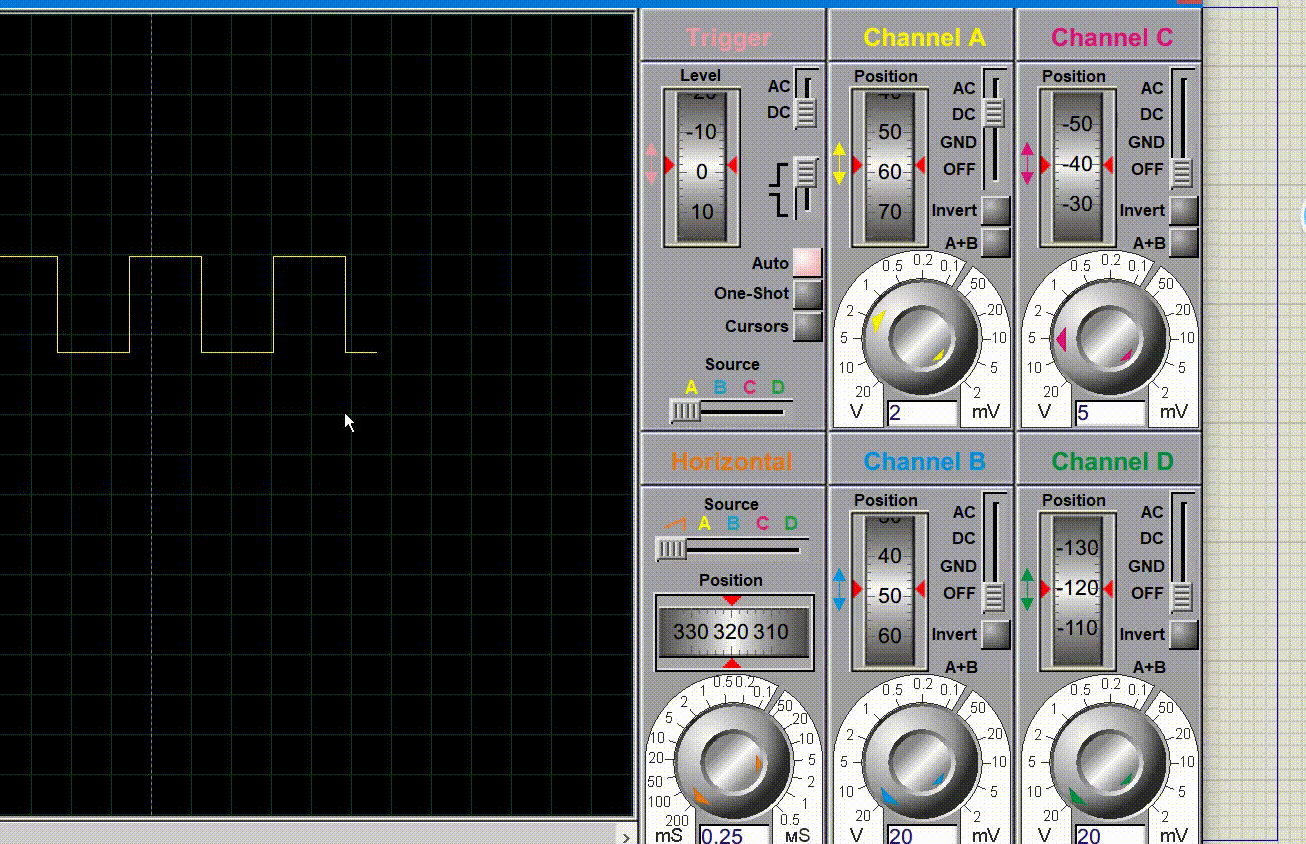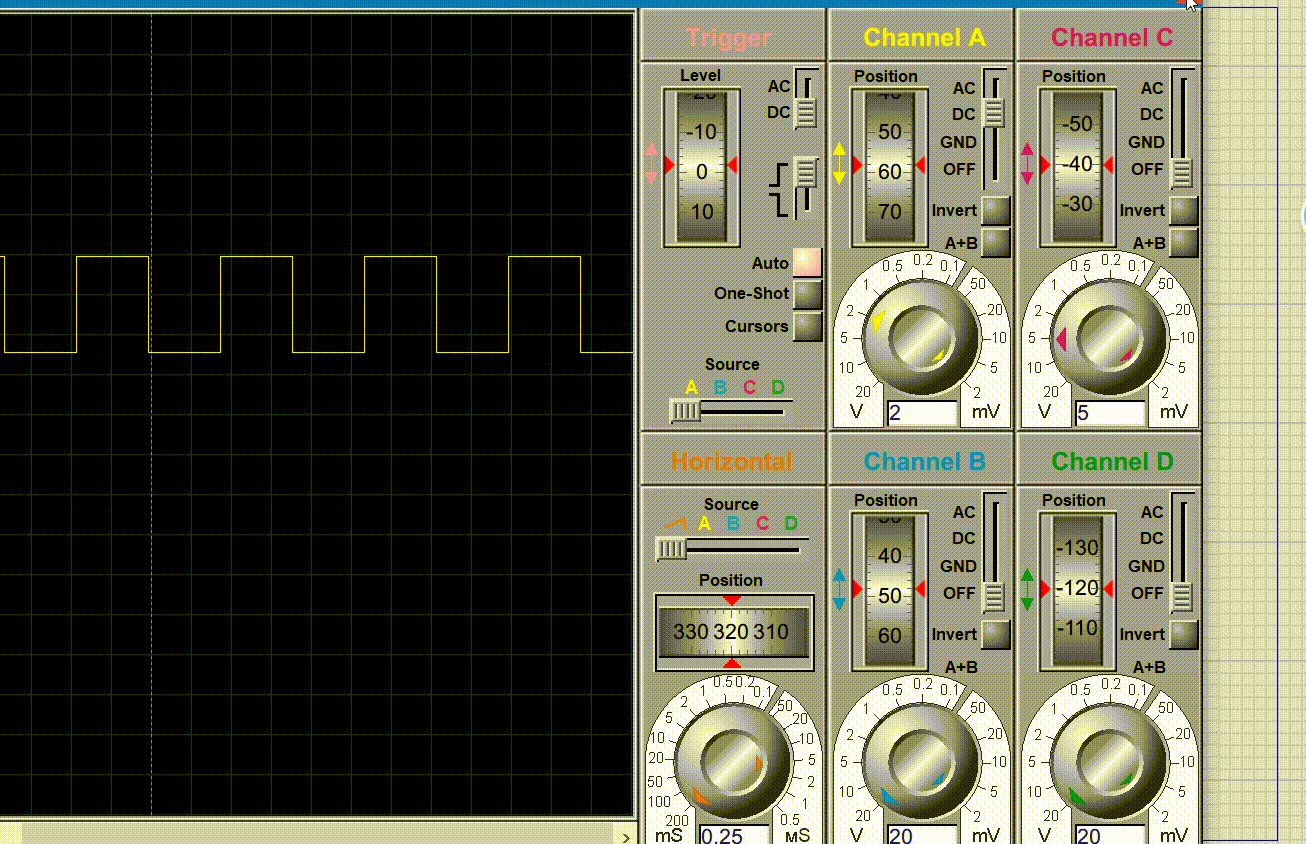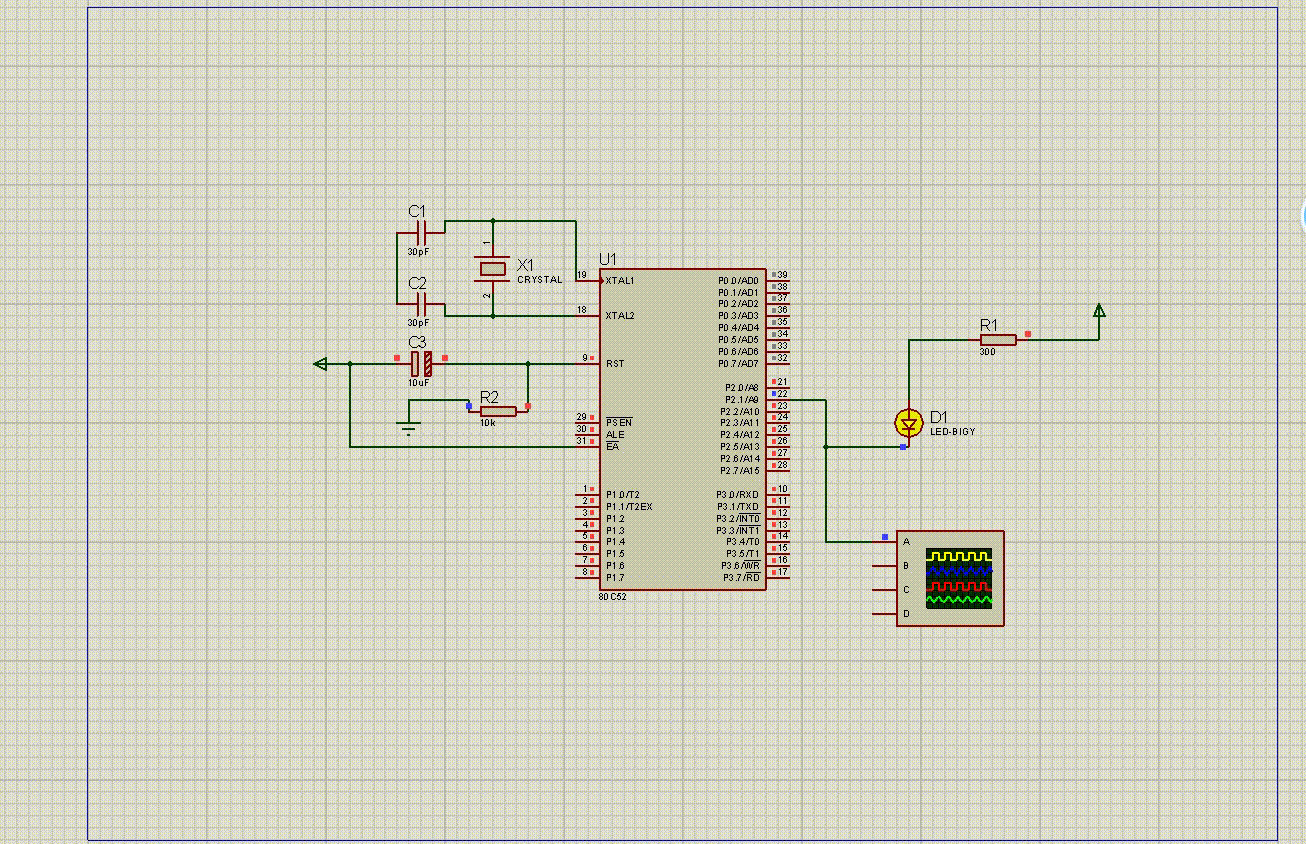
实物演示如下:

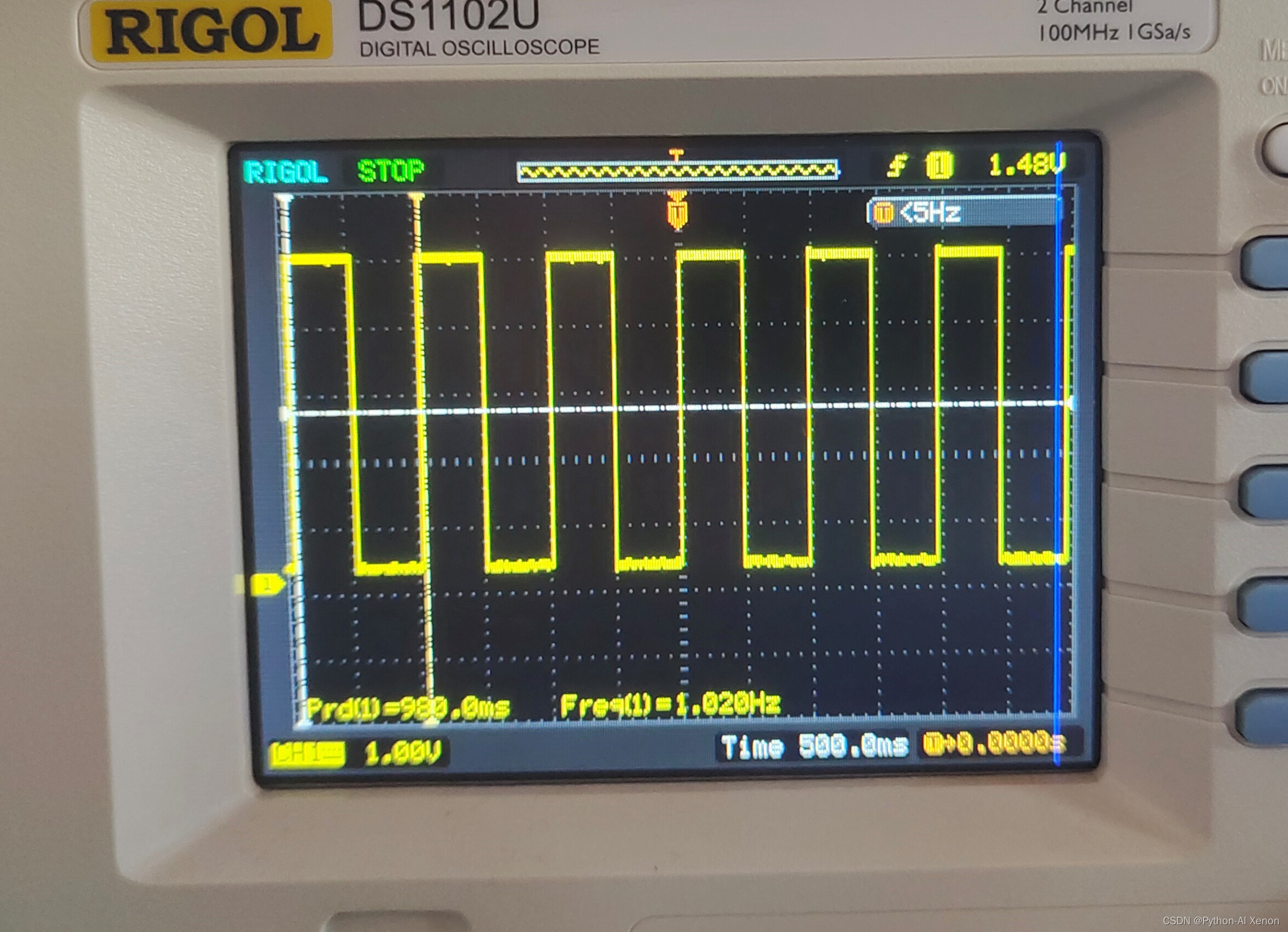
可以见结果符合所需要求.