DDPM

论文

扩散模型包括两个过程：前向过程（forward process）和反向过程（reverse process），其中前向过程又称为扩散过程（diffusion process），如下图所示，从$x_0$到$x_T$的过程。无论是前向过程还是反向过程都是一个参数化的马尔可夫链（Markov chain），其中反向过程可以用来生成数据，这里我们将通过变分推断来进行建模和求解。

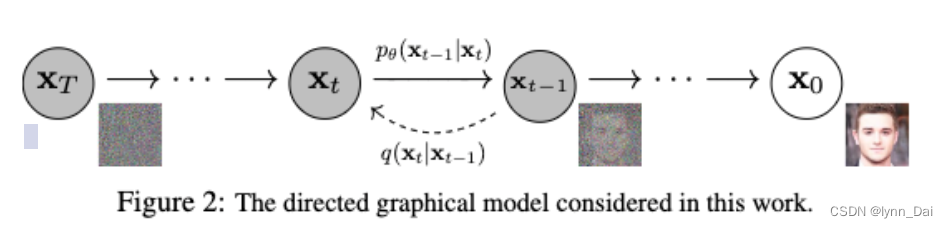
扩散过程

扩散过程是指的对数据逐渐增加高斯噪音直至数据变成随机噪音的过程。对于原始数据$x_0\sim q(x_0)$，总共包含$T$步的扩散过程的每一步都是对上一步得到的数据$x_{t-1}$按如下方式增加高斯噪音：
$$q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_t\mathbf{I})$$
其中，${\beta }_t$是每一步所采用的方差/扩散率，介于0～1之间。随着step的叠加，采用更大的方差。按照超参数处理，β 的范围从0.0001逐步增大到0.02。
扩散过程的每一步都生成一个带噪音的数据$x_t$，整个扩散过程也就是一个马尔卡夫链：
$$q(x_{1:T}|x_0)=\prod _{t=1}^{T}q(x_t|x_{t-1})$$
扩散过程往往是固定的，即采用一个预先定义好的variance schedule，比如DDPM就采用一个线性的variance schedule。
扩散过程的一个重要特性是我们可以直接基于原始数据$x_0$来对任意$t$
步的$x_t$进行采样：$x_t\sim q(x_t|x_0)$。定义${\alpha }_t=1-{\beta }_t$和 $\bar{\alpha }={\prod }_{i=1}^t{\alpha }_i$。通过重参数技巧（和VAE类似），那么有：

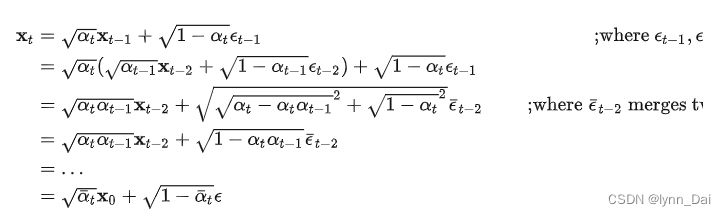
返重参数化后，得到：
$$q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{\overline{{\alpha }_t}}{x}_0,(1-\overline{{\alpha }_t})\mathbf{I})$$
可以看到$x_t$其实可以看成是原始数据$x_0$和随机噪音$ϵ$的线性组合，其中$\sqrt{\overline{{\alpha }_t}}$和$\sqrt{1-\overline{{\alpha }_t}}$为组合系数，它们的平方和等于1，我们也可以称两者分别为signal_rate和noise_rate。我们直接将$\overline{{\alpha }_t}$设定为一个接近0的值，那么就可以保证最终得到的$x_T$近似为一个随机噪音。其次，后面的建模和分析过程将使用这个特性。

a. 为什么扩散率是逐渐增大的呢，也即为什么噪音所占的比例越来越大呢？
在加噪声的过程中，扩散率逐渐增大，对应着在去噪声的过程中，扩散率逐渐减小，也就是说，去噪的过程是先把"明显"的噪声给去除，对应着较大的扩散率；当去到一定程度，逐渐逼近真实真实图像的时候，去噪速率逐渐减慢，开始微调，也就是对应着较小的扩散率
b. 重参数化技巧
如果要对高斯分布$\mathcal{N}(\mu ,{\sigma }^2)$进行采样一个噪声$ϵ$，等价于先从标准正态分布$\mathcal{N}(0,1)$中采样的到一个噪声$\mathbf{z}$，然后对其乘上标准差$\sigma$，加上均值 $\mu$，即$ϵ=\mu +\sigma \cdot \mathbf{z}$。举个例子，上面我们已经得到了${\mathbf{x}}_t$是从高斯分布$\mathcal{N}(\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I})$采样出来的噪声，该高斯分布的均值为$\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1}$标准差为$\sqrt{{\beta }_t}$，所以${\mathbf{x}}_t=\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1}+\sqrt{{\beta }_t}\mathbf{z}$。

反向过程

扩散过程是将数据噪音化，那么反向过程就是一个去噪的过程，如果我们知道反向过程的每一步的真实分布$q(x_{t-1}|x_t)$，那么从一个随机噪音$x_T\sim \mathcal{N}(0,\mathbf{I})$逐渐去噪就能生成一个真实的样本，所以反向过程也就是生成数据的过程。

根据贝叶斯公式：
$$q(x_{t-1}|x_t,x_0)=q(x_t|x_{t-1},x_0)\frac{q(x_{t-1}|x_0)}{q(x_t|x_0)}$$
根据前向过程，已知：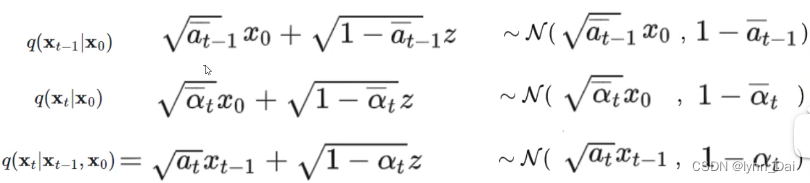
把标准正态分布展开后，乘法相当于加，除法就相当于减。则可以得到分布正比于：
$$\propto exp(-\frac{1}{2}\frac{(x_t-\sqrt{a_t}{x}_{t-1}{)}^2}{{\beta }_t}+\frac{(x_{t-1}-\sqrt{{\bar{a}}_{t-1}}{x}_{t0}{)}^2}{1-{\bar{a}}_{t-1}}-\frac{(x_t-\sqrt{a_t}{x}_0{)}^2}{1-{\bar{a}}_t}))$$
进一步化简，得到 ：

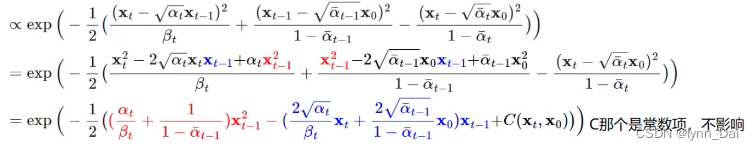
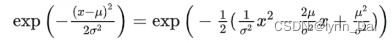
可以得到，后验分布$q(x_{t-1}|x_t,x_0)$的均值和方差：

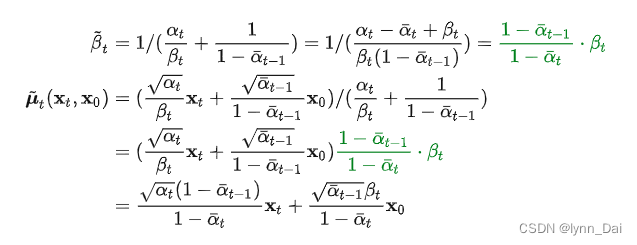
可以看到方差是一个定量（扩散过程参数固定），而均值是一个依赖$x_0$和$x_t$的函数。模型预测在$x_t$在t时刻的噪音$z_t$，求解近似$z_t$

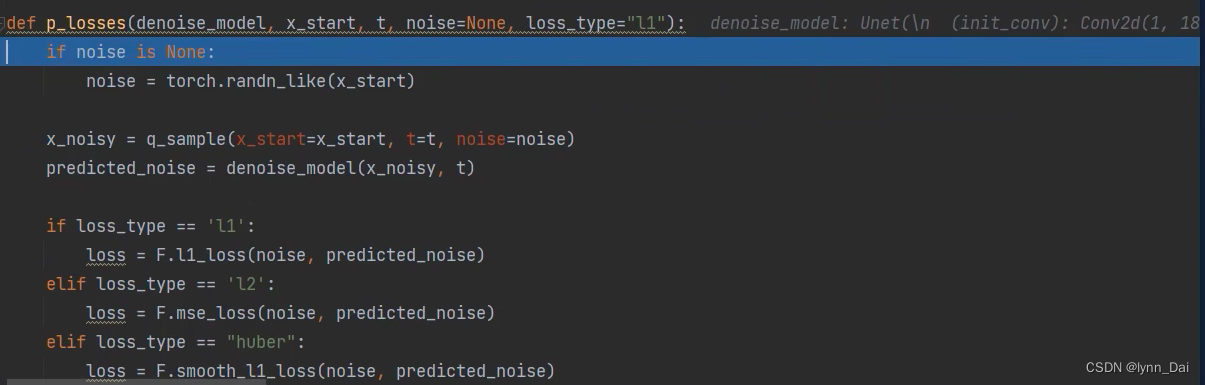
训练部分

• 首先在真实图像分布$q({\mathbf{x}}_0)$，也即我们的训练图像
• 在区间1,…,T中随机生成一个t，代表扩散（加噪）次数
• 在标准正态分布中采样一个随机噪声
• 计算损失函数：让网络预测的噪声与真实的噪声一致。

这里的t做一个时间编码喂入网络中，因为在后向过程中，每一次迭代的网络都是相同的，即参数共享，那怎么让网络知道现在迭代到哪一步呢，那么我们就将t一同传进去参与训练，用t来告诉网络进行到第几次迭代了。时间编码和transformer中的位置编码类似。

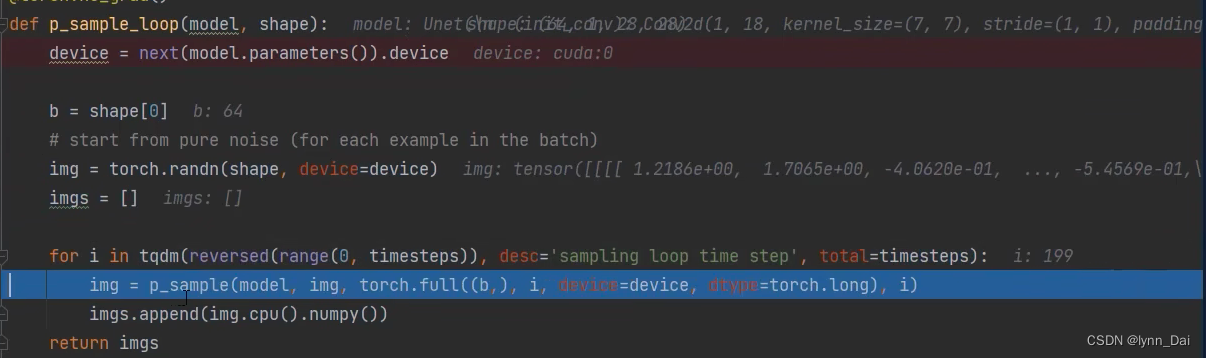
Stable Diffusion

论文
Stable Diffusion基于Latent Diffusion Models，专门用于文图生成任务。
论文贡献

• Diffusion model相比GAN可以取得更好的图片生成效果，然而该模型是一种自回归模型，需要反复迭代计算，因此训练和推理代价都很高。论文提出一种在潜在表示空间（latent space）上进行diffusion过程的方法，从而能够大大减少计算复杂度，同时也能达到十分不错的图片生成效果。
• 相比于其它空间压缩方法，论文提出的方法可以生成更细致的图像，并且在高分辨率图片生成任务（如风景图生成，百万像素图像）上表现得也很好。
• 论文将该模型在无条件图片生成（unconditional image synthesis）, 图片修复（inpainting）,图片超分（super-resolution）任务上进行了实验，都取得了不错的效果。
• 论文还提出了cross-attention的方法来实现多模态训练，使得条件图片生成任务也可以实现。论文中提到的条件图片生成任务包括类别条件图片生成（class-condition）, 文图生成（text-to-image）, 布局条件图片生成（layout-to-image）。这也为日后Stable Diffusion的开发奠定了基础。

Latent Diffusion Models整体框架如图，首先需要训练好一个自编码模型（AutoEncoder，包括一个编码器 $\mathcal{E}$和一个解码器$\mathcal{D}$ ）。这样就可以利用编码器$\mathcal{E}$对图片进行压缩，然后在潜在表示空间上做diffusion操作，最后再用解码器$\mathcal{D}$ 恢复到原始像素空间。论文将这个方法称之为感知压缩（Perceptual Compression）。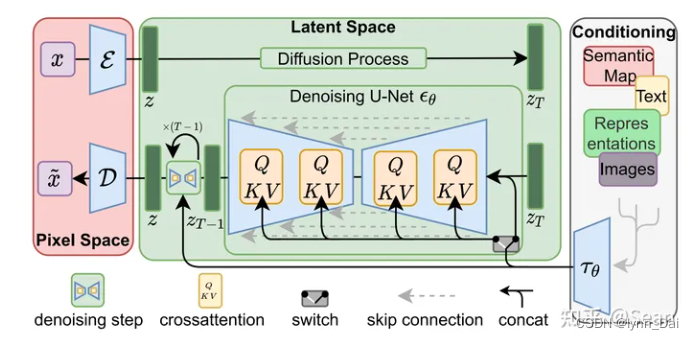
在潜在表示空间上做diffusion操作其主要过程和标准的扩散模型没有太大的区别，所用到的扩散模型的具体实现为 time-conditional UNet。有一个重要的地方是论文为diffusion操作引入了条件机制（Conditioning Mechanisms），通过cross-attention的方式来实现多模态训练，使得条件图片生成任务也可以实现。

图片感知压缩

感知压缩主要利用一个预训练的自编码模型，该模型能够学习到一个在感知上等同于图像空间的潜在表示空间。这种方法的一个优势是只需要训练一个通用的自编码模型，就可以用于不同的扩散模型的训练，在不同的任务上使用。这样一来，感知压缩的方法除了应用在标准的无条件图片生成外，也可以十分方便的拓展到各种图像到图像（inpainting，super-resolution）和文本到图像（text-to-image）任务上。

基于感知压缩的扩散模型的训练本质上是一个两阶段训练的过程，第一阶段需要训练一个自编码器，第二阶段才需要训练扩散模型本身。在第一阶段训练自编码器时，为了避免潜在表示空间出现高度的异化，作者使用了两种正则化方法，一种是KL-reg，另一种是VQ-reg，因此在官方发布的一阶段预训练模型中，会看到KL和VQ两种实现。在Stable Diffusion中主要采用AutoencoderKL这种实现。

具体来说，给定图像$x\in {\mathbb{R}}^{H\times W\times 3}$，先利用一个编码器 $\mathcal{E}$来将图像编码到潜在表示空间$z=\mathcal{E}(x)$，其中$x\in {\mathbb{R}}^{h\times w\times c}$，然后再用解码器从潜在表示空间重建图片$\hat{x}=\mathcal{D}(z)=\mathcal{D}(\mathcal{E}(x))$

潜在扩散模型

扩散模型可以解释为一个时序去噪自编码器，其目标是根据输入去预测一个对应去噪后的变体，或者说预测噪音，相应的目标函数可以写成如下形式：

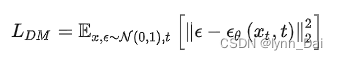
在潜在扩散模型中，引入了预训练的感知压缩模型，它包括一个编码器和一个解码器 。这样就可以利用在训练时就可以利用编码器得到。从而让模型在潜在表示空间中学习，相应的目标函数可以写成如下形式：

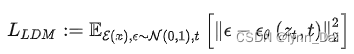
条件机制

除了无条件图片生成外，我们也可以进行条件图片生成，这主要是通过拓展得到一个条件时序去噪自编码器${ϵ}_{\theta }(z_t,t,y)$。

通过$y$来控制图片合成的过程。论文通过在UNet主干网络上增加cross-attention机制来实现。为了能够从多个不同的模态预处理y，论文引入了一个领域专用编码器，它用来将 y 映射为一个中间表示。这样我们就可以很方便的引入各种形态的条件（文本、类别、layout等等）。最终模型就可以通过一个cross-attention层映射将控制信息融入到UNet的中间层，cross-attention层的实现如下：

实验

感知压缩权衡

下采样因子f，$f=H/h=W/w$，如果$f=1$等于没有对输入的像素空间进行压缩，如果$f$越大，则信息压缩越严重，可能会噪声图片失真，但是训练资源占用的也越少。论文对比了$f$在分别 { 1 , 2 , 3 , 4 , 8 , 16 , 32 } \{1,2,3,4,8,16,32\} {1,2,3,4,8,16,32}下的效果，发现$f$在 { 4 − 16 } \{4-16\} {4−16}之间可以比较好的平衡压缩效率与视觉感知效果。作者重点推荐了LDM-4和LDM-8。

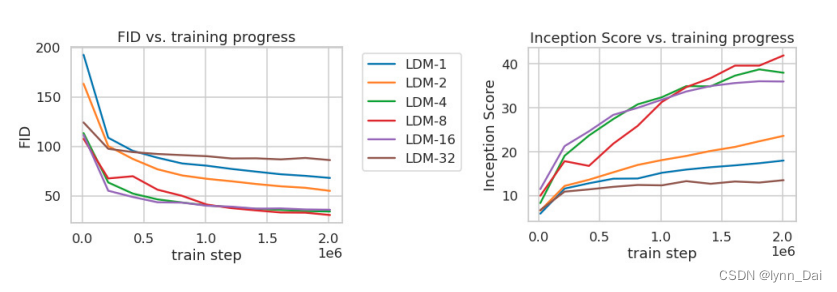
其中：FID(Fréchet Inception Distance)是一种评价GAN的指标，是表示生成图像的多样性和质量，FID越小，则图像多样性越好，质量越好。IS（Inception Score）被用来描述随机性，指标衡量的是生成模型的两个能力：生成图片的质量和生成图片的多样性。

Versatile Diffusion ： Text, Images and Variations All in One Diffusion Model

论文 代码
供一种统一模型去处理：文本到图像、图像到文本生成、图像编辑等多功能扩散模型。

多功能框架需要面向不同任务，这往往需要设计不同模型，因此Versatile Diffusion提出将现有的单流扩散管道扩展为多流网络，这样就能在一个统一的模型中处理文本到图像、图像到文本、图像编辑和文本变体。具体模型结构如下所示：

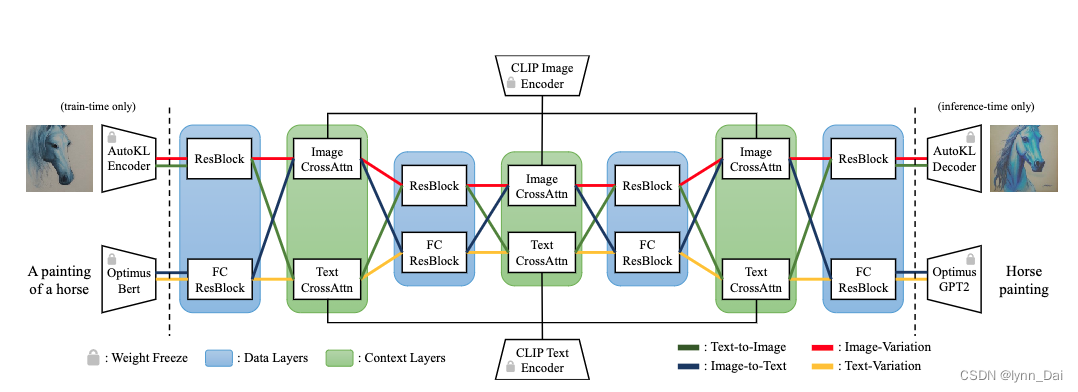
借鉴Stable Diffusion，文章在单流扩散时使用autoKL作为VAEs的编码和解码部分，使用UNet作为噪声预测网络，使用CLIP/Bert作为Context的条件输入。为了统一多流任务，VD包含以下三个部分，

• Diffuser：采用带有cross-attention的UNet网络。即在文到图生成任务下，采用图片UNet和文本的cross-attention上下文；在图到图生成任务下，采用图片的UNet和图片的cross-attention上下文，如上图所示不同颜色的线。
• VAE：图像使用Stable Diffusion相同的Autoencoder-KL，文本使用Bert编码、GPT2解码。
• Context encoder：图像和文本都基于CLIP。

文章将扩散器分为三层：全局层（global layers），数据层（data layers），上下文层（context layers）。例如Stable Diffusion中time-embedding是全局层，残差网络（UNet）是数据层，cross-attention是上下文层。在文到图生成任务下，扩散器采用图片的数据层和文本的上下文；在图到图生成任务下，扩散器采用图片的数据层和图片的上下文。
基于此框架训练时选择一系列的支撑任务来计算所有的loss，并且使用可定制的梯度计算器同时优化每个层。