122.买卖股票的最佳时机II

如果想到其实最终利润是可以分解的，那么本题就很容易了！
如何分解呢？
假如第0天买入，第3天卖出，那么利润为：prices[3] - prices[0]。
相当于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])。
此时就是把利润分解为每天为单位的维度，而不是从0天到第3天整体去考虑！
收集正利润即可

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int sum = 0;
        for(int i = 0; i < prices.size()-1; ++i){
            if(prices[i+1] - prices[i] > 0) sum += prices[i+1] - prices[i];
        }
        return sum;
    }
};

55. 跳跃游戏

自己写想到了用递归，但是本题递归超时。
所以这道题目关键点在于：不用拘泥于每次究竟跳几步，而是看覆盖范围，覆盖范围内一定是可以跳过来的，不用管是怎么跳的。

class Solution {
public:
    bool canJump(vector<int>& nums) {
        if(nums.size() == 1) return true;
        int maxLength = nums[0];
        for(int i = 0; i <= maxLength; ++i){
            if(nums[i] + i > maxLength) maxLength = nums[i] + i ;
            if(maxLength >= nums.size()-1) return true;
        }
        return false;
    }
};

45.跳跃游戏II(本题还很混沌)

所以真正解题的时候，要从覆盖范围出发，不管怎么跳，覆盖范围内一定是可以跳到的，以最小的步数增加覆盖范围，覆盖范围一旦覆盖了终点，得到的就是最小步数！
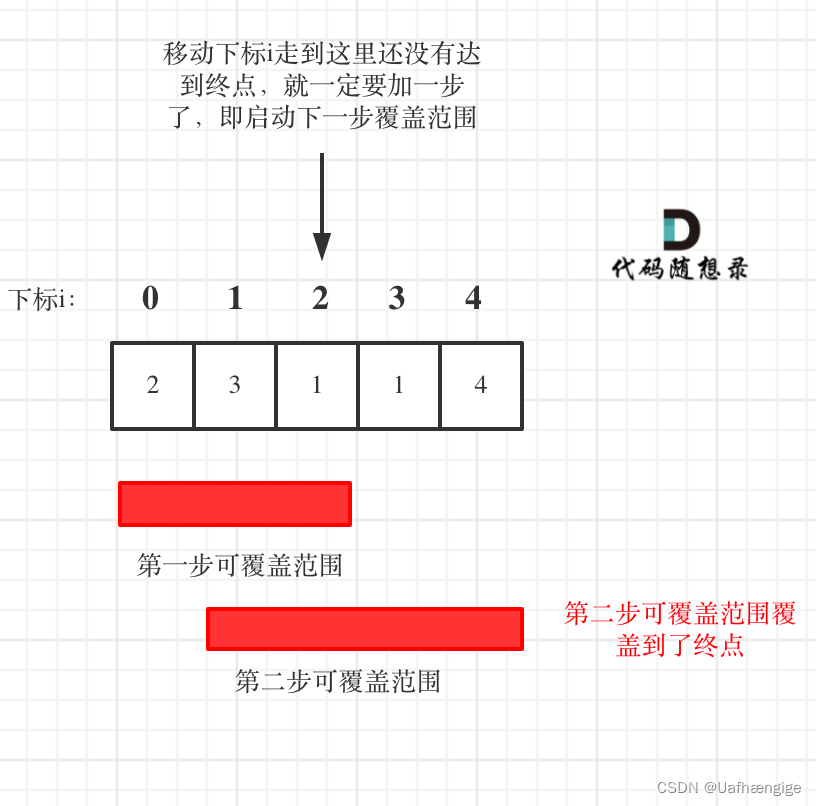最外层的for循环只是在遍历数组，更新当前最大的覆盖范围。真正决定要不要跳一步的时候，是当i = curIndex 的时候，发现还没走到。此时要更新curIndex。当i = curIndex就是走到了当前可以走的最大距离。nextIndex也是在这个范围内更新的。所以此时curIndex = nextIndex，给的就是这个范围内的最大覆盖范围。

class Solution {
public:
    int jump(vector<int>& nums) {
        if(nums.size() == 1) return 0;
        int step = 0;
        int curIndex = 0;
        int nextIndex = 0;
        for(int i = 0; i < nums.size(); ++i){
            nextIndex = max(nextIndex,i+nums[i]);
            if(i == curIndex){
                if(i < nums.size() - 1){
                    step++;
                    curIndex = nextIndex;
                    if(nextIndex >= nums.size()) break;
                }
            }

        }
        return step;
    }
};