⏰【计数排序】

计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用

> 基本思路：
1.统计数据出现的次数
2.根据统计的结果将序列拷贝回到原来的序列中去。

注意：这里需要用到相对位置映射。不能单纯的绝对位置映射。
为什么？因为会有不必要的空间浪费。

待排序数组元素下标0对应着计数数组下标0，待排序元素下标1对应的计数数组下标1，待排序元素下标2对应着计数数组下标2，……待排序元素100的下标，对应着计数数组下标100.
我们需要开辟一个计数数组，专门用来计算每个数据出现的次数，而理论上该数组该开辟多大呢？如果原数组中最大值为10，则拷贝数组开辟10个空间即可。
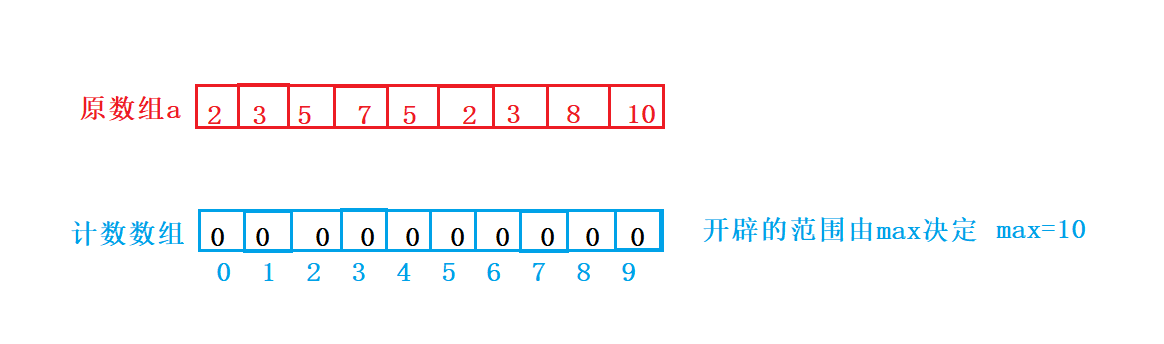
在这里插入图片描述

这里计数数组开辟后，需要全部初始化为0.

首先我们需要对原数组进行计算，统计每个数据出现的次数。
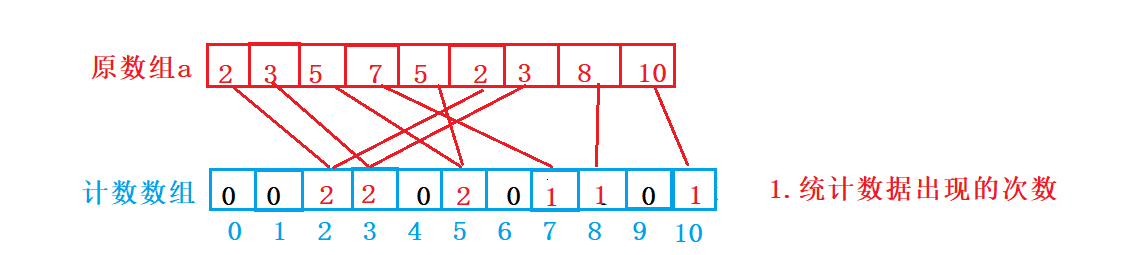
在这里插入图片描述
然后我们根据计数数组里的数据来进行排序

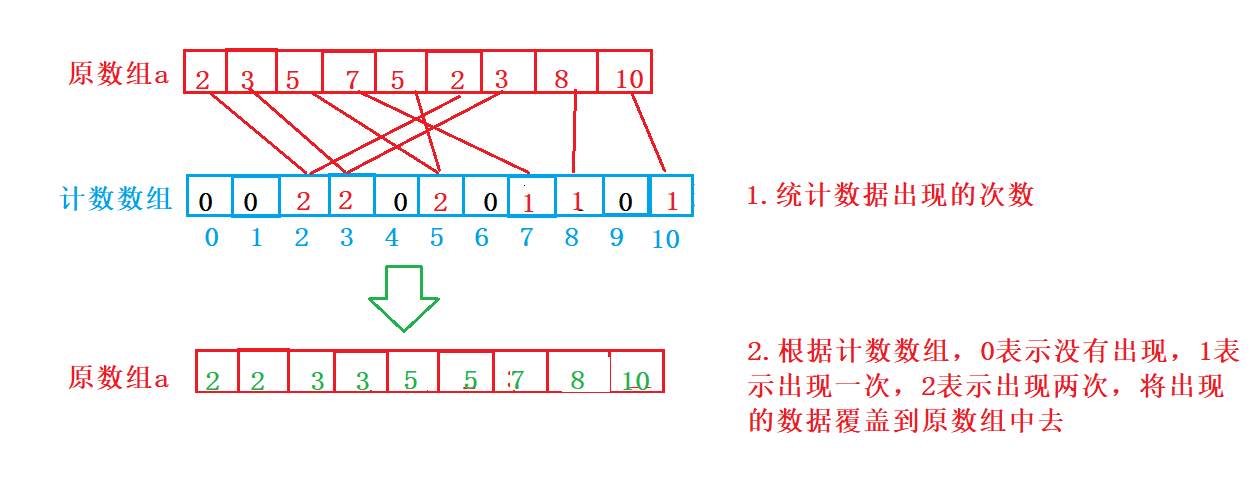
这种是属于决定位置映射，而当数据很大时，比如最大值为100时，就需要计数数组开辟100个空间，而最小值为90值，那么前90个空间就相当于浪费了。

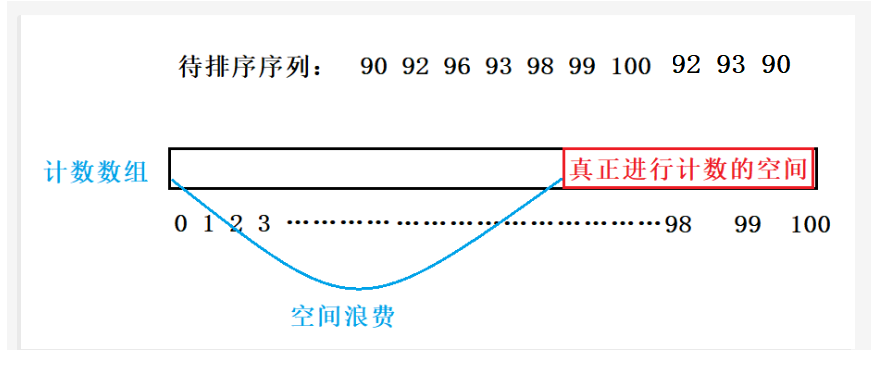
所以我们需要使用相对位置映射。这样可以减少空间的浪费。
即计数数组空间大小的开辟取决于待排序序列中的最大值和最小值。它的范围就是range=最大值-最小值+1.
这样前面的空间就不会开辟浪费了。
在这里插入图片描述

只不过待排序数组在计数数组中的位置是相对的。
比如待排序数组-最小值才是在计数数组的位置。
比如90-最小值=0.它在计数数组中就是下标为0的值
92-最小值=2，它在计数数组中就是下标为2的值
100-最小值=10，它在计数数组中就是下标为10的值。
在这里插入图片描述

🕐计数

第一步：统计每个数据出现的次数
1.遍历待排序数组，将最大值最小值获取出来
2.开辟计数数组
3.初始化计数数组
4.计数

void Countsort(int *a,int n)//计数排序O(N+range)
{
	int i = 0;
	int max = a[i], min = a[i];
	for (i = 1; i < n; i++)//遍历一遍原数组
	{
		if (a[i] > max)
		{
			max = a[i];
		}
		if (a[i] < min)
		{
			min = a[i];
		}
	}
	int range = max - min + 1;//计数数组开辟的大小由range确定

	int* counta = (int*)calloc(range,sizeof(int));//初始化计数数组都为0
	//calloc在开辟空间的同时也为数组初始化为0 
	
	//memset(counta, 0, sizeof(int) * range);也可以用memset初始化数组
	for (int i = 0; i < n; i++)
	{
		counta[a[i] - min]++;//相对位置映射
		//a[i]-最小值，是待排序数据在计数数组中的位置
	}

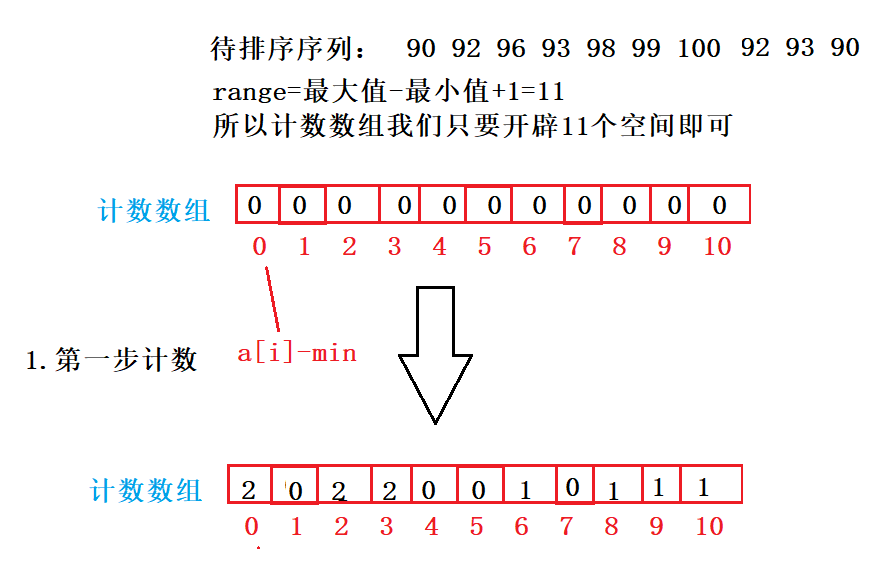
在这里插入图片描述
对于计数数组各个位置上的值，代表这个位置上的值出现了几次，1代表出现1次，2代表出现2次，3代表出现3次，0代表没有出现。

🕦排序

第二步：根据计数数组，对原数组进行覆盖

	int j = 0;
	for (int i = 0; i  < range; i++)
	{
		while (counta[i]--)//出现几次就往原数组放几次
		{
			a[j++] = i + min;//因为是相对位置映射，i位置上的数据并不真正是i而是i+min，将出现几次覆盖到原数组上去。
		}
	}

🕓测试

void Countsort(int *a,int n)//计数排序O(N+range)
{
	int i = 0;
	int max = a[i], min = a[i];
	for (i = 1; i < n; i++)//遍历一遍原数组
	{
		if (a[i] > max)
		{
			max = a[i];
		}
		if (a[i] < min)
		{
			min = a[i];
		}
	}
	int range = max - min + 1;

	int* counta = (int*)calloc(range,sizeof(int));//初始化计数数组都为0
	//memset(counta, 0, sizeof(int) * range);
	for (int i = 0; i < n; i++)
	{
		counta[a[i] - min]++;
	}
	//对计数数组排序,覆盖原数组
	//这个位置的值，代表了这个值出现了几次 1代表出现一次，2代表出现两次
	int j = 0;
	for (int i = 0; i  < range; i++)
	{
		while (counta[i]--)
		{
			a[j++] = i + min;//出现几次就往原数组放几次
		}
	}
}
int main()
{
	int a[] = { 90，92，96，93，98，99，100，92，93，90};
	int n = sizeof(a) / sizeof(a[0]);
	Countsort(a,n);
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	return 0;
}