文章目录
- 并行分布式计算 并行算法与并行计算模型
- 基础知识
- 定义与描述
- 复杂性度量
- 同步和通讯
- 并行计算模型
- PRAM 模型
- 异步 PRAM 模型 (APRAM)
- BSP 模型
- LogP 模型
- 层次存储模型
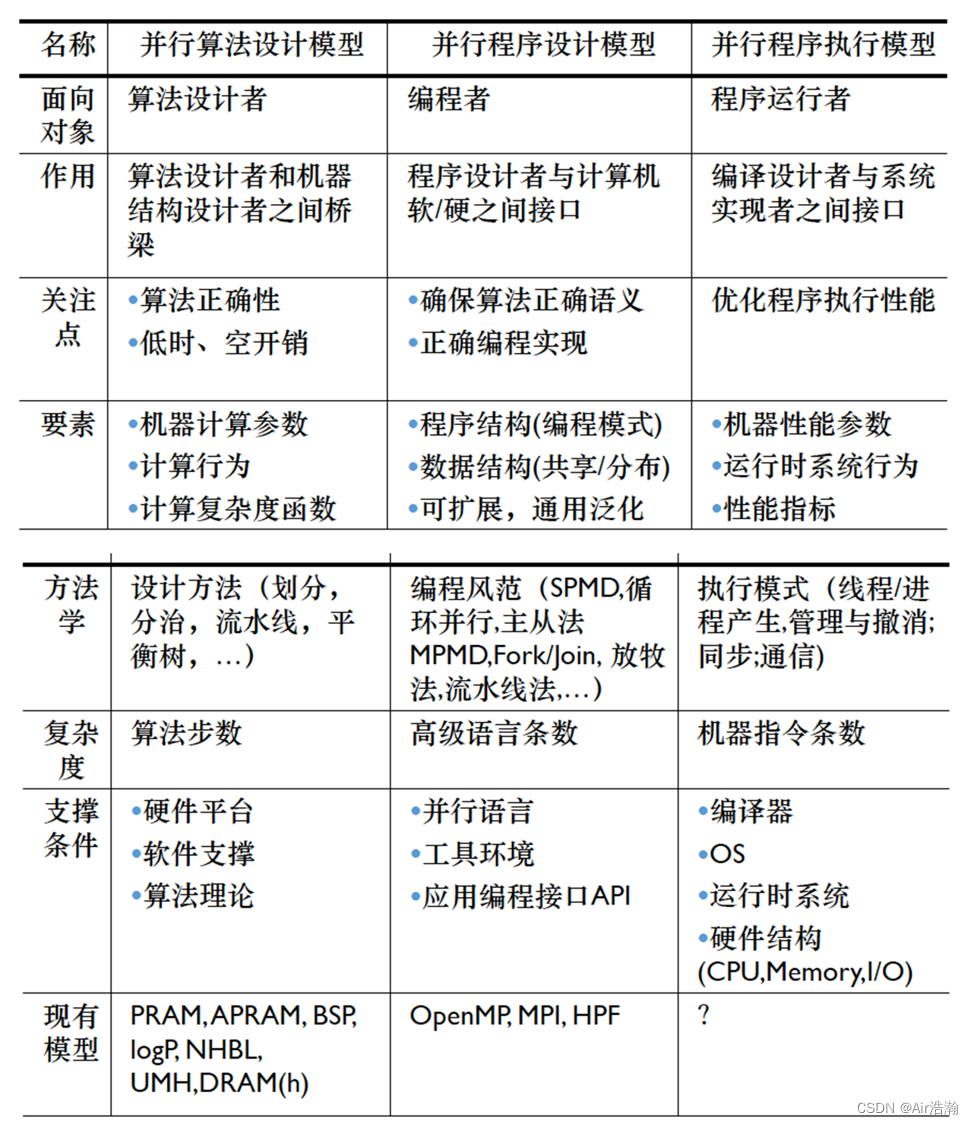
- 分层并行计算模型
并行分布式计算 并行算法与并行计算模型
基础知识
定义与描述
并行计算模型类型:抽象计算模型和使用计算模型
并行算法类型:
- 数值计算(代数关系运算)、非数值计算(比较关系运算)
- 同步算法(算法诸进程的执行必须相互等待)、异步算法(算法诸进程的执行不必相互等待)
- 确定算法、随机算法
Tip:
- 同步算法使得并行执行步骤可预测,需要额外的协议进行保障,同时使得计算效率下降;
- 异步算法执行效率高,但容易发生数据上的冲突
描述语言:
-
Par-do 语句:代表算法的若干步要并行执行
for i = i to n par-do: ... end for -
for all 语句:几个处理器同时执行相同的操作:
for all Pi where 0 <= i <= k do: ... end for
复杂性度量
常用的复杂性度量指标:
- 运行时间 t(n) :(n 为问题实例的输入规模)包含计算时间和通讯时间,分别用计算时间步和选路时间步作为单位;
- 处理器数 p(n)
- 并行算法成本 c(n) :c(n)=t(n)p(n) ;
- 成本最优性 :若 c(n) 等于在最坏请形下串行算法所需要的时间,则并行算法是成本最优的;
- 总运算量:并行算法求解问题时所完成的总的操作步骤
Tip:并行算法的总成本肯定比串行算法要高(需要通信、数据传递等),但我们的目标往往是 t(n) 的降低;
Brent 定理 :令 W ( n ) W(n) W(n) 是某并行算法 A 在运行时间 T ( n ) T(n) T(n) 内所执行的运算量,则 A 使用 p 台处理器可在 t ( n ) = O ( W ( n ) / p + T ( n ) ) t(n)=O(W(n)/p+T(n)) t(n)=O(W(n)/p+T(n)) 时间内执行完毕
Tip:当 p = c ( n ) W ( n ) p=\frac{c(n)}{W(n)} p=W(n)c(n) 时, W ( n ) W(n) W(n) 和 c ( n ) c(n) c(n) 渐进一致,其他情况下并不一定都能充分有效地利用处理器去工作,因此设计并行算法时应尽可能将每个时间步的工作量均匀地分摊给 p 台处理器,使各处理器处于活跃状态。
同步和通讯
同步:时间上强制使得各执行进程在某一点必须相互等待;在异步执行过程中,为了确保正确执行顺序,需要设置适当同步点;
通信:空间上对各并发执行的进程执行数据交换,使用通信原语来表达:
global read(X, Y)
global write(U, V)
Send(X, i)
Receive(Y, j)
并行计算模型
PRAM 模型
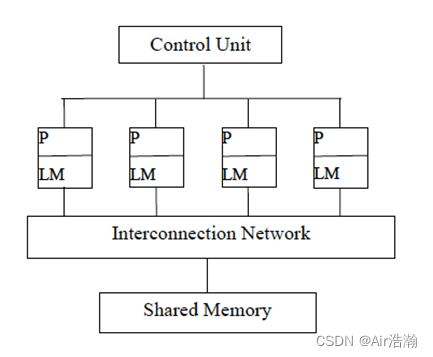
PRAM:并行随机存储机器,即共享存储器的 SIMD 模型
- 假定存在一个容量无限大的共享存储器
- 有限或无限个功能相同的处理器
- 任何时刻各处理器均可以通过共享存储单元相互交换数据
分类:根据读和写是否是并发或互斥进行分类,并发读并发写(PRAM-CRCW)是最强的计算模型,而互斥读互斥写(PRAM-EREW)可以
log
p
\log{p}
logp 模拟并发度互斥写(PRAM-CREW)进而并发读并发写:
T
E
R
E
W
≥
T
C
R
E
W
≥
T
C
R
C
W
T
E
R
E
W
=
O
(
T
C
R
E
W
⋅
log
p
)
=
O
(
T
C
R
C
W
⋅
log
p
)
T_{EREW}\geq T_{CREW} \geq T_{CRCW} \\ T_{EREW} = O(T_{CREW}\cdot \log{p}) = O(T_{CRCW}\cdot \log{p})
TEREW≥TCREW≥TCRCWTEREW=O(TCREW⋅logp)=O(TCRCW⋅logp)
优点:适合并行算法表示以及复杂度分析,易于使用;隐藏了并行机的通讯、同步等细节;
缺点:不适合 MIMD 并行机,忽略了共享存储的竞争、通讯延迟等因素;
例:并行加法
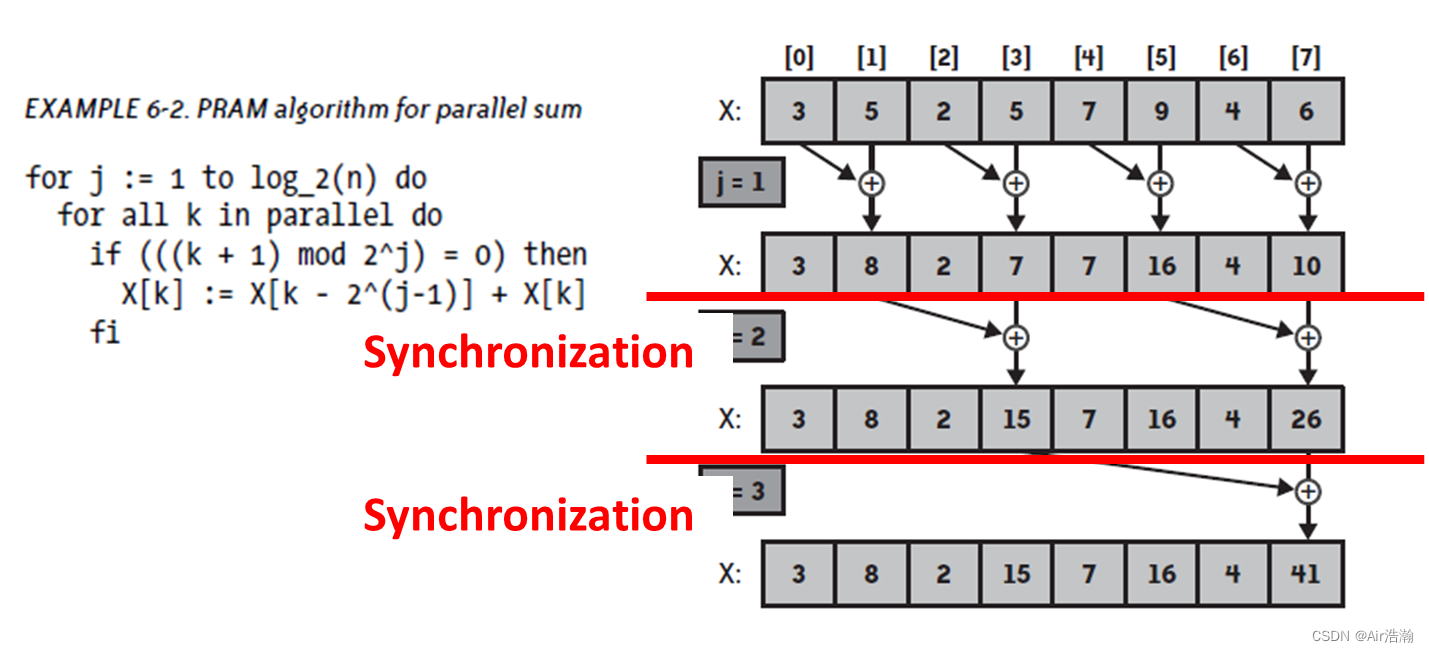
- fi 就是同步的操作
- 这里的算法十分浪费,k 个线程只有一半在工作
异步 PRAM 模型 (APRAM)
APRAM:又称为 分相(Phrase)PRAM 或 MIMD-SM
- 由 p 个处理器组成,每个处理器都有其局部存储器、局部时钟、局部程序;
- 无全局时钟,各处理器异步执行;
- 处理器通过共享存储器进行通讯;(还是保留了 SM)
- 处理器间依赖关系,需要在并行程序中显式地加入同步路障(我觉得叫同步屏障比较合理hh,Synchronization Barrier);
- 一条指令可以在非确定(无界)但有限的时间内完成;
计算过程:
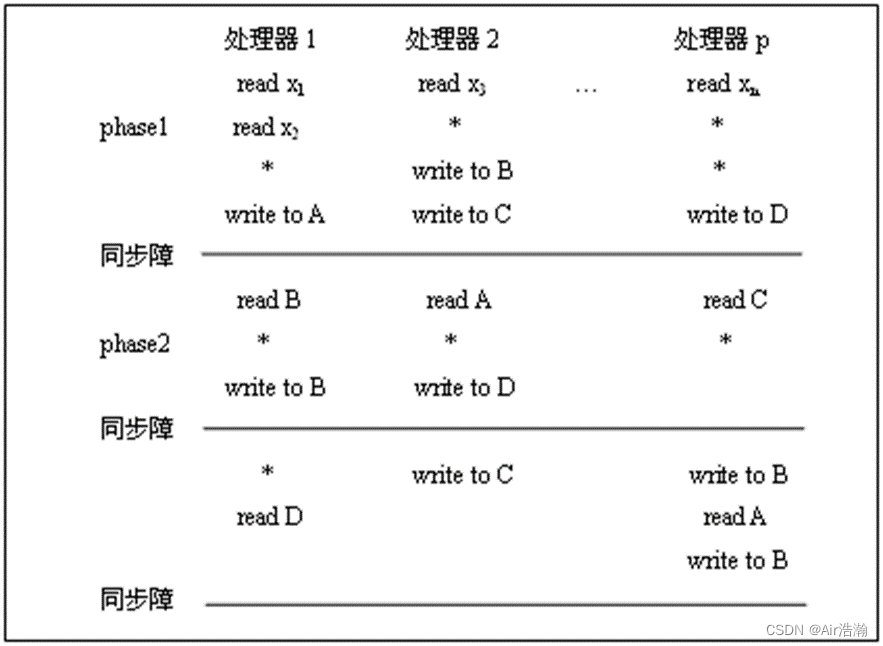
指令类型:全局读、全局写、局部操作、同步
计算时间:

- 需要将任务平均分配, t p h t_{ph} tph 才会降下来
优缺点:
- APRAM 相比于 PRAM 更接近实际的并行机,可以模拟 MIMD 模型,基本建模了单机多核多线程的环境;
- 保留了易编程和分析算法的复杂度,但与现实差距较远;
- 在 APRAM 上可以
- 使用的并行算法非常有限,也不适合 MIMD-DM 模型(因为 APRAM 还是保留了 SM)
BSP 模型
BSP:块同步模型
- APRAM 也称为轻量同步模型,主要是因为SM了所以轻量,所以 BSP 需要通讯;
- 异步 MIMD-DM 模型:支持分布式存储、消息传递系统、块内异步并行、块间显式同步;
计算过程:计算由全局同步、周期为 L 的若干超级步组成。周期间做全局检查,如果没有全部做完。则下一个 L 周期分配给未曾完成的超级步。
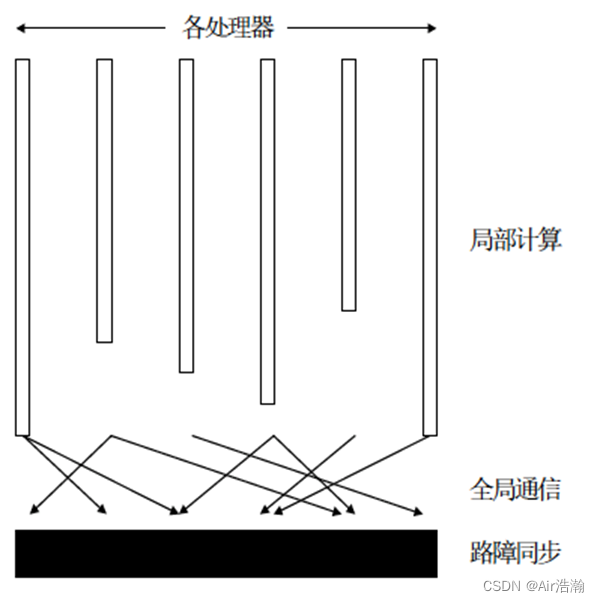
模型参数:
- p:处理器数(带有存储器)
- L:同步障时间
- g:带宽因子(1/bandwidth),即每个 packet 传输需要多少时间
优缺点:
- 相比于 SM,将处理器和选路器分开,强调了计算和通讯的分离;
- 选路器仅实行点到点的消息传递,掩盖了具体网络协议,简化通信协议;
- 采用路障方式,用硬件实现可控粗粒度的全局同步;但是需要显式同步机制,限制至多 h 条消息的传递等;
- 提供了一个编程环境(比如下面求前缀和的框架),利于程序复杂度分析
例:Prefix Scan

LogP 模型
LogP:分布存储的、点到点通信的多处理机模型
- PRAM、APRAM、BSP 都没有充分考虑到数量多且强大的处理器/存储器节点,也没有考虑到带宽受限的、延迟可观的互联网络(BSP 虽然引入了网络通讯,但是只有一个参数带宽因子 g)
模型参数:(不涉及网络的具体结构)
- 延迟 L:网络中消息从源到宿所产生的延迟;
- 额外开销 o:处理器发送或接受一条消息所需的额外开销;
- 最小时间间隔 g:处理器连续进行消息发送或接受的最小时间间隔
- 模块数 P:处理器/存储器 模块数
特点:
- L 和 g 反映了通讯网络的容量,和 o 一起刻画了网络通信特征;
- 屏蔽了网络拓扑、选录算法和通信协议等具体细节(是合理的,在上千个处理器在网络轻载时,对网络和结构也不敏感)
- 每个节点只有一个处理器,发送/接受消息要付出开销 o,对于长消息提供专门硬件支持,对消息长度无特别处理;
- 最普遍的全局操作是路障;
BSP vs. LogP :
- BSP 是块同步,而 LogP 是进程对同步;
- BSP 可以常数因子模拟 LogP,LogP 可以对数因子模拟 BSP;
- BSP= LogP + Barriers - Overhead;
- BSP 提供了更方便的程设环境,更简便,复合结构化编程;LogP 更好地利用了机器资源,更符合实际情况;
总结:
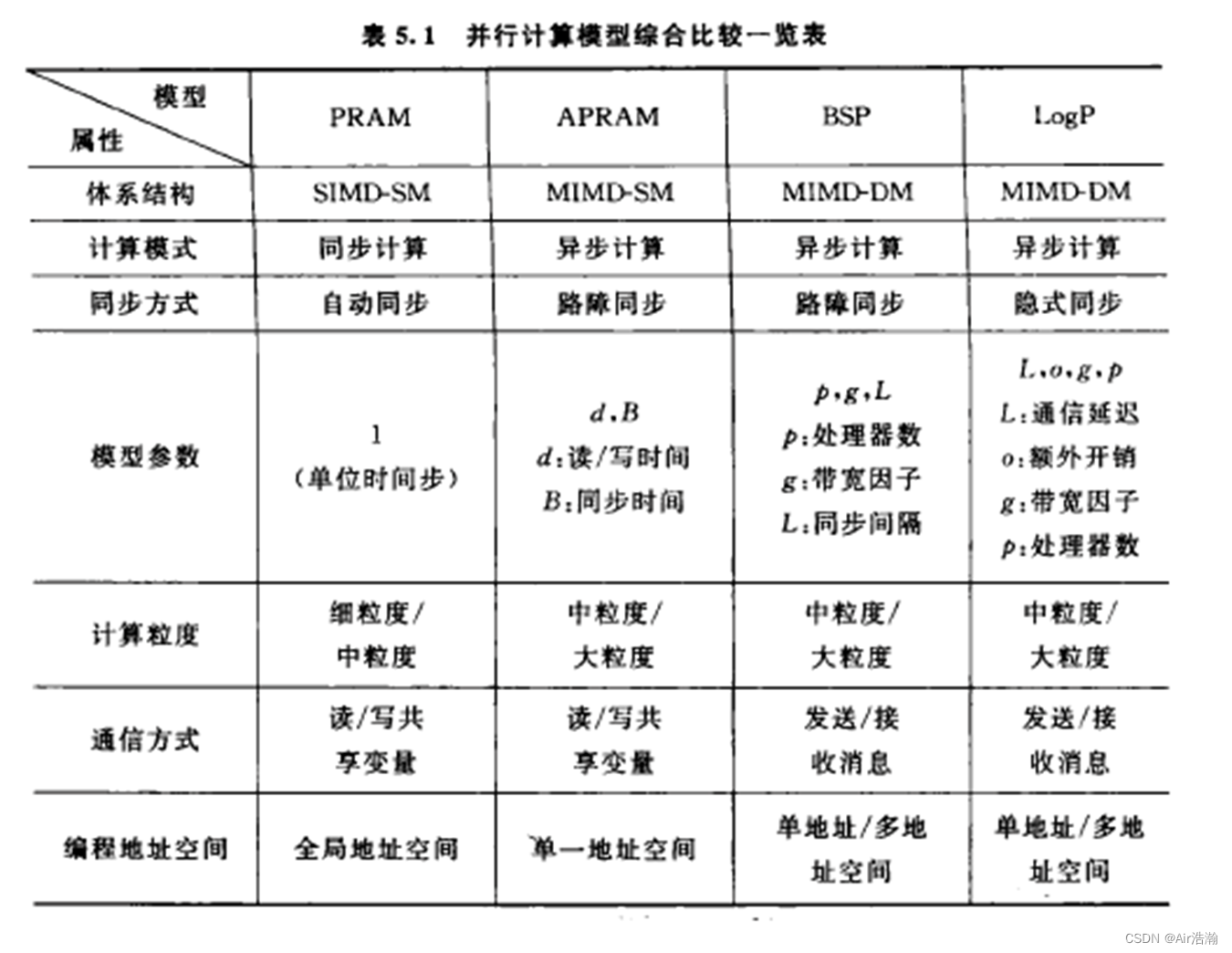
层次存储模型
并行计算模型均假定存储系统具有一级主存,且访问时间均为单位时间(本机一定有自己的存储),但是存储系统是分层的,访存均视为单位时间是不精确地。
串行计算系统的层次存储模型 :
- HMM (Hierarchical Memory Model)和 HMM-BT (with Block Transfer):面向地址,访问数据的地址决定了访存开销;-BT 增加了块传输,数据的地址处于什么块也会影响开销;该模型对顺序访问有效;
- UMA(Uniform Memory Hierachy,均匀存储层次):每层的开销是固定的
- RAM(h) 模型:单层随机访问存储,可以推广到 h-层存储,各层访问开销是非均匀一致的。
并行计算系统的层次存储模型 :
- Memory-LogP:将 LogP 中网络延迟参数 L 扩展到通信开销函数,函数参数为应用数据集合大小和数据分布;
- DRAM(h) :分布式 RAM(h) 模型,以 RAM(h) 为本地存储,消息传递视为另一层存储层次访问(远端的数据当作新的一层),DRAM(h)=RAM(h)+LogP;
- HPM:层次并行和存储,描述同构并行系统中的层次并行性和层次存储特性
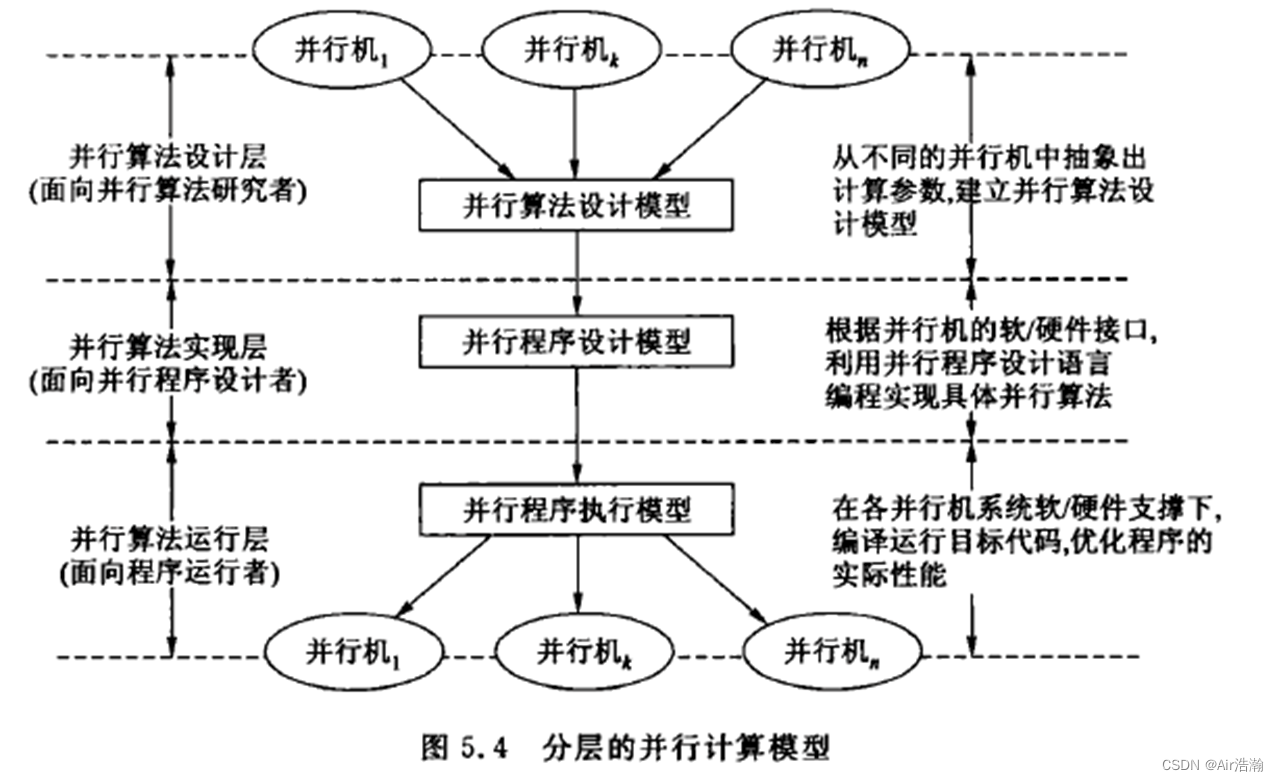
分层并行计算模型