1、直接选择排序

1.1 排序思路

选择排序的思想非常简单：每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

选择排序的步骤：

在元素集合 array[i]−−array[n−1] 中选择最大(小)的数据元素，若它不是这组元素中的最后一个(第一个)元素，则将它与这组元素中的最后一个（第一个）元素交换

在剩余的 array[i]−−array[n−2]（array[i+1]−−array[n−1]）集合中，重复上述步骤，直到集合剩余 1个元素

下面用动图展示过程：
在这里插入图片描述

1.2 代码实现

假设我们排升序，那么每次就要选最小数的下标mini ，遍历数组，找出 mini ，然后交换，让起始位置begin++ ，直到begin=n 停止，此刻数组就有序了。

void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
void SelectSort(int* a, int n)
{
	// 选 1 个数
	int begin = 0;

	while (begin < n)
	{
		int mini = begin;

		for (int i = begin + 1; i < n; i++)
		{
			if (a[i] < a[mini])
			{
				mini = i;
			}
		}

		Swap(&a[begin], &a[mini]);
		begin++;
	}
}

这是单次选 1个数的情况，实际上我们还可以一次选两个数mini 和maxi 对应最小和最大值

这里代码需要做出一些改变，增加一个终止位置 end 。循环找 mini 和maxi ，每次找到之后交换begin 和 mini 对应的值和 end 和 maxi 对应的值，将begin++,end−− ，直到 begin≥end 。

注意
假设序列已经找到了mini 和maxi ：

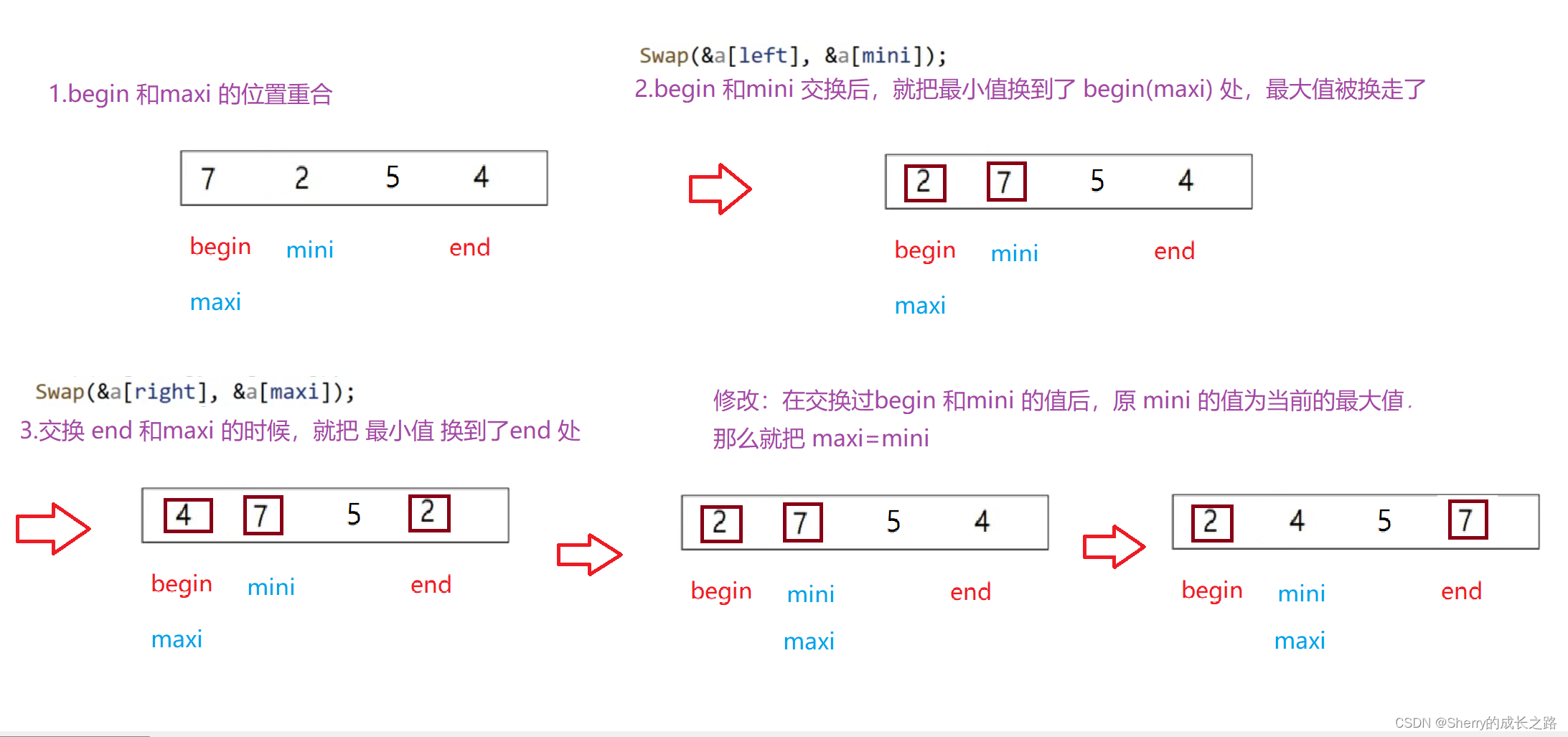
在这里插入图片描述

begin 和maxi 的位置重合了，那么begin 和mini 在交换的时候，就把最小值换到了 begin(maxi) 处，最大值被换走了。那么接下来交换 end 和maxi 的时候，就把最小值换到了end 处。

这就导致了排序错误，在 begin==maxi 时，在交换过begin 和mini 的值后，原 mini 的值为当前的最大值，那么就把 maxi=mini ，让最大值下一次能交换到正确的位置。

void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
void SelectSort(int* a, int n)
{
	int begin = 0, end = n - 1;

	while (begin < end)
	{
		int mini = begin, maxi = begin;

		for (int i = begin + 1; i <= end; i++)
		{
			if (a[i] < a[mini])
			{
				mini = i;
			}

			if (a[i] > a[maxi])
			{
				maxi = i;
			}
		}

		Swap(&a[begin], &a[mini]);
		// 特殊处理
		//当a数组里第1个元素是最大值时，此时经过上面的Swap，最大值的位置已经更改了，所以需要修正最大值的位置，让下一个Swap正确交换
        if (begin == maxi)
		{
			maxi = mini;
		}
		Swap(&a[end], &a[maxi]);
		begin++;
		end--;
	}
}

1.3 特性及复杂度

选择排序无论是选单边，还是两边一起选，时间复杂度都是 O(N^2)。
因为总是要每次遍历选出最小或最大下标，然后进行数据交换。

所以选择排序的效率是不太行的，一般不常用，但是它的思路很简单。

空间复杂度是O(1) ，因为没有开辟额外空间。

特性：
直接选择排序逻辑好理解，但效率不是很好，实际中很少使用。
时间复杂度：O(N^2) 。
空间复杂度：O(1) 。
稳定性：不稳定。

2、堆排序

2.1 排序思路

堆排序算法基本思想：是利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种，通过堆来进行数据选择。需要注意的是，排升序要建大堆（大根堆），排降序建小堆（小根堆）。

2.2 代码实现

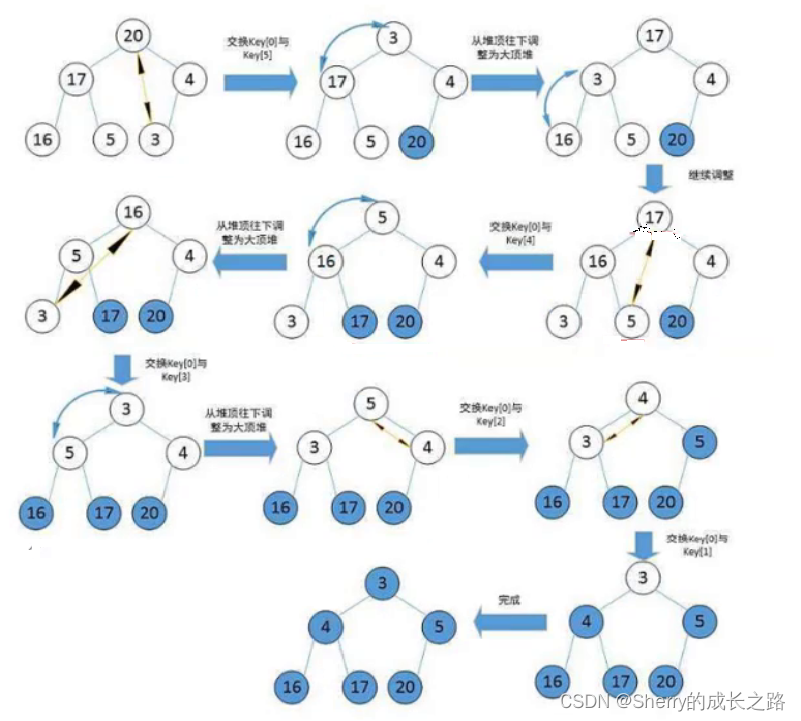
1.首先通过向下调整或向上调整的方式建堆，推荐向下调整，因为效率更高，具体原因及复杂度分析看这篇博客：【树与二叉树】堆的时间复杂度详解以及堆的应用—堆排序、TOP - K问题
向上调整建堆：模拟插入的过程
向下调整建堆：模拟删除的过程，这里从倒数的第一个非叶子节点开始调整
在这里插入图片描述

2.堆创建后，如何进行排序 (升序、降序)
升序建大堆；降序建小堆。不是说升序建小堆；降序建大堆不行，而是因为不好：
如果排升序建小堆：
1、选出最小的数，最小的数就放在第一个位置
2、接着就要选次小的数，再选次小的数 … … 不断的选下去，如何选？
只能对剩下的 sz-1、sz-2、sz-3 … 个数继续建堆。可想这样的代价是很高的 —— 建堆的时间复杂度是 O(N)，整个时间复杂度就是 O(N^2)，堆的价值没有体现，不如直接循环遍历
在这里插入图片描述
如果排升序建大堆：
1、选出最大的数，与最后一个数交换位置
2、怎么选出次大、次次大？
堆的结构没有被破坏，且最后一个数不看做堆，左右子树依旧是大堆，向下调整即可
最多调整 log₂N 次，整体的时间复杂度是 O(N*log₂N）
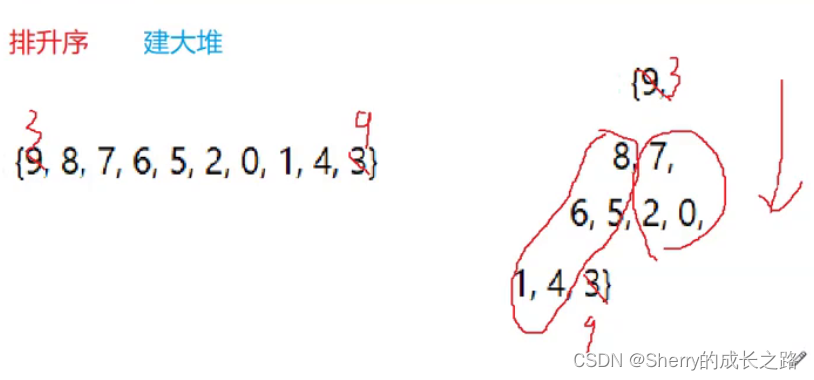
在这里插入图片描述

综上：升序建大堆、降序建小堆
在这里插入图片描述

//实现父子交换的函数
void Swap(int* px, int* py)
{
	int temp = *px;
	*px = *py;
	*py = temp;
}
//实现调整
void AdjustDown(int* arr, int sz, int parent)
{
	//确定左孩子的下标
	int child = parent * 2 + 1;
	//孩子的下标超出数组的范围就停止
	while (child < sz)
	{
		//确定左右孩子中较小/大的那个
			//左孩子大于右孩子，所以让child记录较小孩子的下标 || (arr[child]<arr[child+1]记录较大孩子的下标)
		if (arr[child] > arr[child + 1] && child + 1 < sz)
		{
			child++; //(当只有一个左孩子时，会越界，且后面使用时会发生非法访问)
		}
		//判断父亲和小孩子
			//小孩子小于父亲，则交换，且继续调整 || (arr[child]>arr[parent]大孩子大于父亲，则交换，且继续调整)
		if (arr[child] < arr[parent])
		{
			Swap(&arr[child], &arr[parent]);
			//迭代
			parent = child;
			//重新确定左孩子的下标(当最后的叶子节点是parent时，这时去确定child会以读的方式越界，但可以不关心)
			child = parent * 2 + 1;
		}
		//小孩子大于父亲，则停止调整
		else
		{
			break;
		}
	}
}
//堆排序 -> 效率更高
void HeapSort(int* arr, int sz)
{
	//建堆
	int i = 0;
	//从最后一棵树开始调整，也就是最后一个节点的父亲
	for (i = (sz - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(arr, sz, i);
	}
}