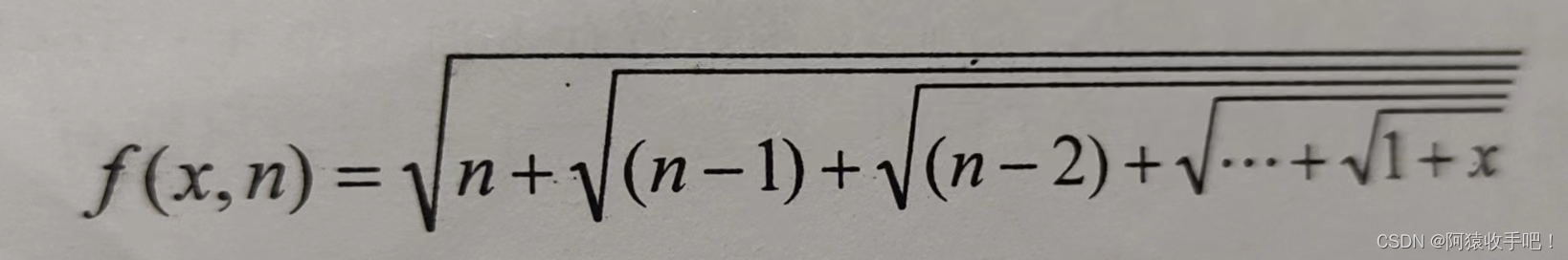Harris角点
opencv函数
cornerHarris提取输入图像的Harris角点
检测原理
检测思想:使用一个固定窗口在图像上进行任意方向的滑动,对比滑动前后的窗口中的像素灰度变化程度,如果存在任意方向上的滑动,都有较大灰度变化,则认为该窗口中存在角点。
E ( u , v ) = ∑ ( x , y ) ∈ W w ( x , y ) [ I ( x + u , y + v ) − I ( x , y ) ] 2 E(u, v)=\sum_{(x, y) \in W} w(x, y)[I(x+u, y+v)-I(x, y)]^{2} E(u,v)=∑(x,y)∈Ww(x,y)[I(x+u,y+v)−I(x,y)]2
当窗口滑动时,滑动前后对应的窗口中的像素点灰度变化为
E
(
u
,
v
)
E(u, v)
E(u,v)
对
E
(
u
,
v
)
E(u, v)
E(u,v)进行泰勒展开,对公式进行化简,最终得到:
E ( u , v ) = [ u v ] M [ u v ] E(u, v)=\left[\begin{array}{ll}u & v\end{array}\right] M\left[\begin{array}{l}u \\ v\end{array}\right] E(u,v)=[uv]M[uv]
其中M为:
M = ∑ ( x , y ) ∈ W w ( x , y ) [ I x 2 I x I y I x I y I y 2 ] M = \sum_{(x, y) \in W} w(x, y)\left[\begin{array}{cc}I_{x}^{2} & I_{x} I y \\I_{x} I_{y} & I_{y}^{2}\end{array}\right] M=∑(x,y)∈Ww(x,y)[Ix2IxIyIxIyIy2]
I x I_x Ix为图像在x方向的梯度,y方向同理。
如果M没有梯度变化较大的点,则当前没有角点或边缘点。如果M只在一个方向上有梯度变化很大的点,则当前可能只有边缘点。若M在xy方向上均变换很大,则当前框内有角点。
角点相应得分:
R
=
det
(
M
)
−
k
(
trace
(
M
)
)
2
R=\operatorname{det}(M)-k(\operatorname{trace}(M))^{2}
R=det(M)−k(trace(M))2
其中
det
(
M
)
=
λ
1
λ
2
\operatorname{det}(M)=\lambda_{1} \lambda_{2}
det(M)=λ1λ2
trace
(
M
)
=
λ
1
+
λ
2
\operatorname{trace}(M)=\lambda_{1}+\lambda_{2}
trace(M)=λ1+λ2
k k k在0.04到0.06之间。 λ 1 λ 2 \lambda_{1} \lambda_{2} λ1λ2为 M M M的两个特征值。
Harris角点性质
- 增大K值可以降低角点检测的灵敏度,减少被检测角点的数量
- Harris角点对亮度和对比度变化不灵敏
- Harris角点具有旋转不变性
- Harris角点不具有尺度不变性
FAST角点
opencv函数
fast = cv.FastFeatureDetector_create(threshold,nonmaxSuppression)
kp = fast.detect(Img, None)
cv.drawKeypoints (image,keypoints,outputimage,color,flags)
检测原理
取图像中的检测点,以该点为圆心的周围邻域内像素点判断检测点是否为角点。如果圆上有连续N个点的亮度大于或者小于阈值(如选取检测点的亮度的120%或80%),则认为该检测点为特征点。根据N的取值分为FAST-9,FAST-12等。
FAST加速方法
在FAST-12中可以检测圆上第1、5、9、13的像素的亮度,如果这四个像素中有三个同时大于或小于阈值,则该检测点才有可能是特征点,否则直接排除。
非极大值抑制
FAST角点会出现扎堆的现象,因此在第一遍检查过后还要使用非极大值抑制,在一定区域内仅保留响应极大值的角点,避免角点集中的问题。
FAST特征点性质
FAST特征点不具有方向信息和尺度信息。所以ORB在FAST基础上添加了图像金字塔解决尺度问题,添加灰度质心法解决特征的旋转问题。
SIFT特征点
src = cv.imread("123.png")
cv.namedWindow("input", cv.WINDOW_AUTOSIZE)
cv.imshow("input", src)
sift = cv.xfeatures2d.SIFT_create()
kps = sift.detect(src)
result = cv.drawKeypoints(src, kps, None, (0, 0, 255), cv.DrawMatchesFlags_DEFAULT)
cv.imshow("sift-detector", result)
SIFT原理
大致来说就是将图像进行多次下采样,构建出图像金字塔。
但是每层金字塔不止一张图像,而是类似于下面的一组图像。

原理是使用一个变化尺度的高斯函数与原图像进行卷积:
L
(
x
,
y
,
σ
)
=
G
(
x
,
y
,
σ
)
∗
I
(
x
,
y
)
L(x, y, \sigma)=G(x, y, \sigma) * I(x, y)
L(x,y,σ)=G(x,y,σ)∗I(x,y)
其中高斯函数为:
G
(
x
,
y
,
σ
)
=
1
2
π
σ
2
e
−
(
x
−
m
/
2
)
2
+
(
y
−
n
/
2
)
2
2
σ
2
G(x, y, \sigma)=\frac{1}{2 \pi \sigma^{2}} e^{-\frac{(x-m / 2)^{2}+(y-n / 2)^{2}}{2 \sigma^{2}}}
G(x,y,σ)=2πσ21e−2σ2(x−m/2)2+(y−n/2)2
然后
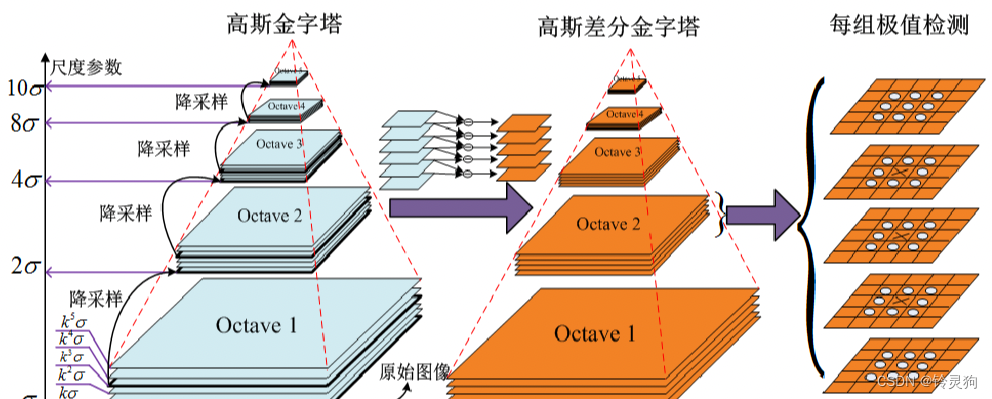
画叉的特征点需要和本层的8个点外加上下两层的9个点共26个点比较,若为最大值或最小值,则认为该点是初步判断的一个特征点。
关键点剔除工作
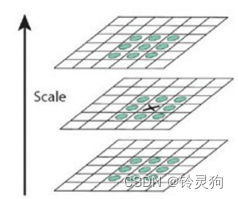
因为我们得到的特征点可能并不是真正的极值点,因此我们将得到离散空间点进行拟合,求出真正的极值点。
我们将检测得到的特征点反复的向计算出的极值点的方向进行偏移(实际是导数为0的方向),排除掉超出设定的迭代次数依然不能收敛的特征点和超出图像边界的特征点。同时也要排除数值小于某个经验值的特征点(如小于0.03或0.04),因为这种数值小的点容易收到噪声的干扰。
这步完成后,我们还需要去掉边缘点。我们初步检测出来的特征点有很多都是在边缘处,因为边缘点有较大的响应,但是这种响应也只发生在一个方向,因此采用了类似于Harris角点的检测方法,求出该检测点在两个方向的Hession矩阵,计算Hession矩阵的特征值,如果两个特征值的和的平方除以两特征值的积小于设定的阈值(如1.2),则认为该点并不是边缘点,保留。

主方向分配
简单点说就是求出特征点的所有邻域梯度的方向,然后统计一下,哪种方向最大则认为该特征点的梯度方向,再选一个大于主梯度80%的方向作为辅方向,增加鲁棒性。
描述子
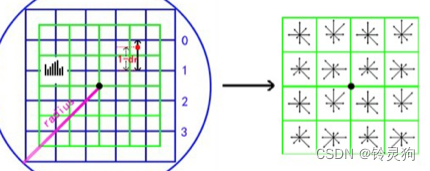
在关键点的44的窗口中计算分别计算八个方向的梯度作为该特征点的描述子,维度为44*8=128维
检测匹配方法
Kd平衡二叉树,查找与目标图像的特征点最邻近的原图像特征点和次邻近的原图像特征点
SIFT特征点性质
- 检测非常稳定,应用广泛
- 计算量大,很难做到实时
SURF特征点
opencv函数
img = cv.imread('photo.png',0)
surf = cv.xfeatures2d.SURF_create(400)
kp, des = surf.detectAndCompute(img,None)
len(kp)
检测原理(类比SIFT)
Hessian矩阵近似
给定图像中一点,可以确定如下的Hessian矩阵:
H
(
x
,
y
,
σ
)
=
(
L
x
x
L
x
y
L
x
y
L
y
y
)
H(x, y, \sigma)=\left(\begin{array}{ll} L_{x x} & L_{x y} \\ L_{x y} & L_{y y} \end{array}\right)
H(x,y,σ)=(LxxLxyLxyLyy)
其中
σ
\sigma
σ为尺度大小
计算Hessian矩阵的行列式值DoH为:
det
H
=
L
x
x
L
y
y
−
L
x
y
2
\operatorname{det} H=L_{x x} L_{y y}-L_{x y}^{2}
detH=LxxLyy−Lxy2
因为此处是对Hessian矩阵进行处理,所以会自动过滤掉边缘点。
检测时选择不同大小的
σ
\sigma
σ生成不同的高斯卷积模版,同样生成图像金字塔,然后在不同位置空间和尺度空间搜索DoH的峰值(同样是26个点),并进行非极大值抑制,得到图像的极值点。
实际运用中对高斯滤波和行列式的计算进行了简化
与SIFT特征点不同的
- SURF并没有通过降采样的方式得到不同尺寸大小的图像建立金字塔,而是借助于不同的 σ \sigma σ构造金字塔。
- 特征点的主方向SIFT在方形邻域窗口内统计梯度方向直方图,而SURF在圆形区域内计算各个扇形范围内的方向,取响应累加和最大的扇形方向。
- 特征描述子,SIFT将关键点附近的邻域划分成4*4的区域,统计每个子区域的梯度方向直方图,统计成128维特征向量。SURF将20乘20像素点的邻域划分成4乘4个子块,计算每个子块的Haar小波响应,并统计4个特征量,得到4乘4乘4=64维度的特征向量。
BRIEF描述子
描述子原理
BRIEF是一种二进制的描述子,其描述向量是0和1表示的二进制串。0和1表示特征点邻域内两个像素(p和q)灰度值的大小:如果p比q大则选择1,反正就取0。在特征点的周围选择128对这样的p和q的像素对,就得到了128维由0,1组成的向量。
BRIEF使用随机选点的比较,速度很快,而且使用二进制串表示最终生成的描述子向量,在存储以及用于匹配的比较时都是非常方便的,其和FAST的搭配起来可以组成非常快速的特征点提取和描述算法。
ORB特征点提取opencv特征点与匹配
源代码来源
import cv2 as cv
def ORB_Feature(img1, img2):
# 初始化ORB
orb = cv.ORB_create()
# 寻找关键点
kp1 = orb.detect(img1)
kp2 = orb.detect(img2)
# 计算描述符
kp1, des1 = orb.compute(img1, kp1)
kp2, des2 = orb.compute(img2, kp2)
# 画出关键点
outimg1 = cv.drawKeypoints(img1, keypoints=kp1, outImage=None)
outimg2 = cv.drawKeypoints(img2, keypoints=kp2, outImage=None)
# 显示关键点
# import numpy as np
# outimg3 = np.hstack([outimg1, outimg2])
# cv.imshow("Key Points", outimg3)
# cv.waitKey(0)
# 初始化 BFMatcher
bf = cv.BFMatcher(cv.NORM_HAMMING)
# 对描述子进行匹配
matches = bf.match(des1, des2)
# 计算最大距离和最小距离
min_distance = matches[0].distance
max_distance = matches[0].distance
for x in matches:
if x.distance < min_distance:
min_distance = x.distance
if x.distance > max_distance:
max_distance = x.distance
# 筛选匹配点
'''
当描述子之间的距离大于两倍的最小距离时,认为匹配有误。
但有时候最小距离会非常小,所以设置一个经验值30作为下限。
'''
good_match = []
for x in matches:
if x.distance <= max(2 * min_distance, 30):
good_match.append(x)
# 绘制匹配结果
draw_match(img1, img2, kp1, kp2, good_match)
def draw_match(img1, img2, kp1, kp2, match):
outimage = cv.drawMatches(img1, kp1, img2, kp2, match, outImg=None)
cv.imshow("Match Result", outimage)
cv.waitKey(0)
if __name__ == '__main__':
# 读取图片
image1 = cv.imread('1.png')
image2 = cv.imread('2.png')
ORB_Feature(image1, image2)
VINS前端光流法
vins-mono前端流程
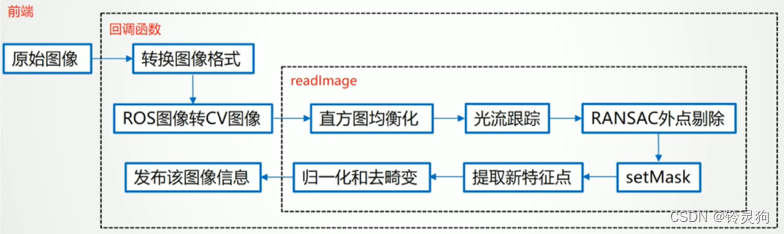
光流追踪:基于灰度不变假设,以上一帧的特征点坐标为起点,在当前帧的同样的坐标下以一定范围找到与上一帧特征点附近区域灰度值相近的区域。
图像金字塔:vins中把上一层图像金字塔追踪的结果作为下一帧图像金字塔追踪的初值。保证了像素精度又保证了追踪结果在还原时的准确度。