差分方程
Z变换
脉冲传递函数
计算机控制系统的响应

---

差分方程

基础知识

几种不同的差分：

前向差分和后向差分没有本质区别，在控制系统中一般用后向差分。

在连续系统中，用微分方程来描述系统的运动。而在离散系统，则使用差分方程：

差分方程是确定时间序列的方程，因为可以通过递推迭代的方法，用前项求后项：

离散系统的差分方程标准形式：(注意各系数的下标)

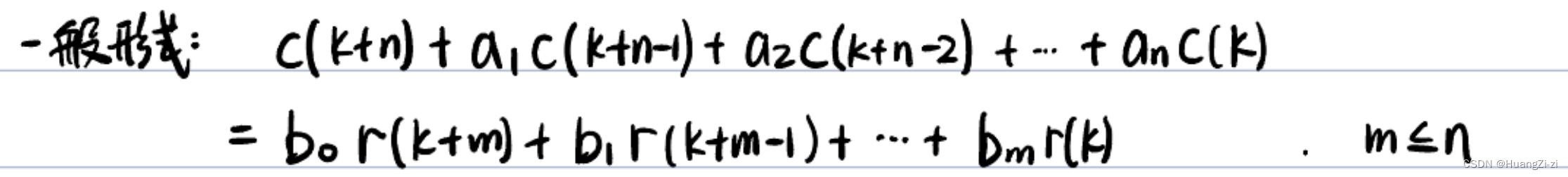
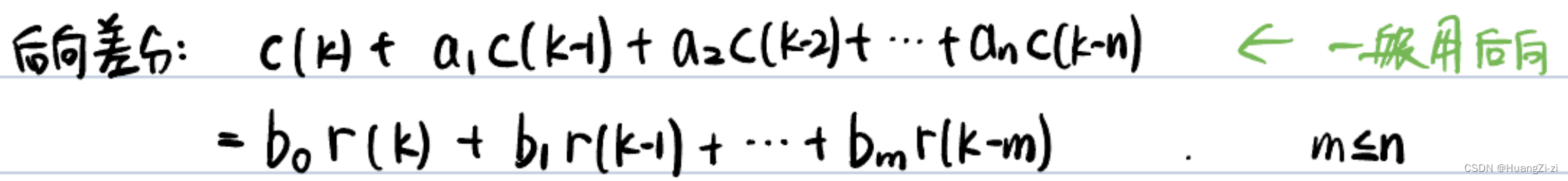
差分方程的解

解分为通解和特解。通解是与方程初始状态有关的解。特解是与外部输入有关的解。

解的求法：

求解特征方程，得到特征根：

1. n个单根$r_1,r_2,r_3,\cdots ,r_n$，则通解
   $y(k)=c_1{r}_1^k+c_2{r}_2^k+\cdots +c_n{r}_n^k$
2. 解$r$为$m$重根，其他为单根$r_1,r_2,r_3,\cdots ,r_n$，则通解：
   $y(k)=c_{11}{r}^k+c_{12}k{r}^k+\cdots +c_{1m}{k}^{m-1}{r}^k+c_1{r}_1^k+c_2{r}_2^k+\cdots +c_n{r}_n^k$

其中各系数根据初始条件来求：

对于后向差分，步骤类似：

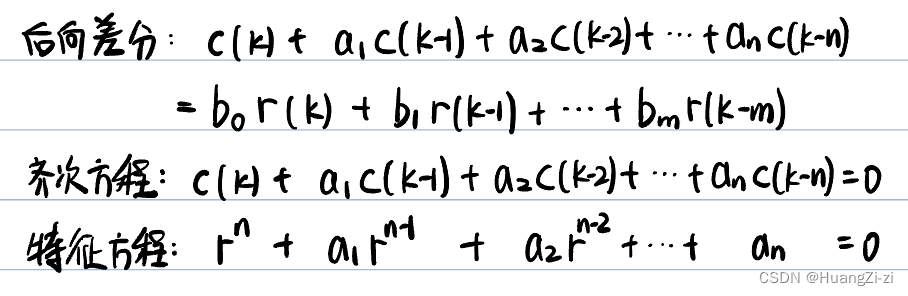
Z变换

定义与性质

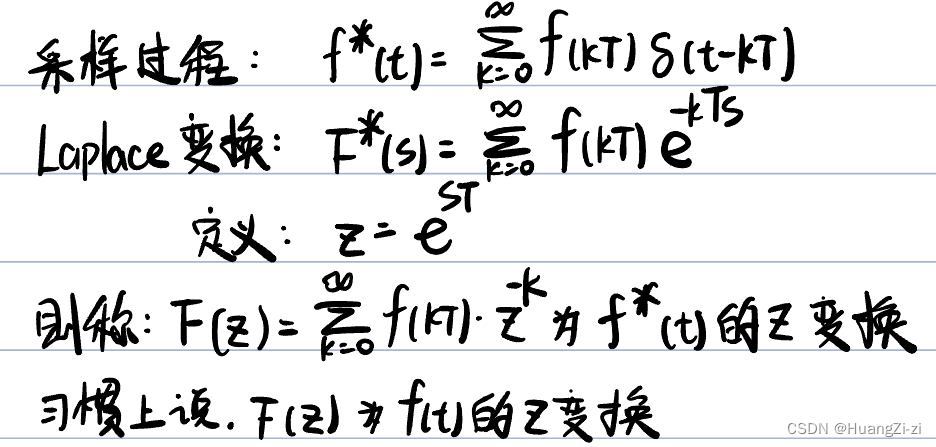
注意：

1. 先采样，然后才有Z变换。多个不同的$f(t)$，如果采样后$f^{\ast }(t)$相同，则Z变换相同
2. $z^{-1}$代表信号滞后一个采样周期，可以称为单位延迟因子
3. 书写时T可以省略，写作$F(z)={\sum }_{k=0}^{\infty }f(k)z^{-k}$

性质：
这里只涉及一部分常用的性质。

1. 线性性质
   $Z[af(kT)+bg(kT)]=aF(z)+bG(z)$
2. 实位移定理
   • 右位移：$Z[f(kT-nT)]=z^{-n}F(z)$
   • 左位移：$Z[f(kT+nT)]=z^n[F(z)-{\sum }_{k=0}^{\infty }f(kT)z^{-k}]$
     • n=1: $Z[f(kT+T)]=z[F(z)-f(0)]$
     • n=2: $Z[f(kT+2T)]=z^2[F(z)-f(0)-f(T)z^{-1}]$
3. 复位移定理
   $Z[e^{\mp at}f(kT)]=F(z{e}^{\pm aT})$
4. 初值定理
   如果极限$\underset{z\to \infty }{\lim }F(z)$存在，则有$f(0)=\underset{z\to \infty }{\lim }F(z)$
5. 终值定理
   设系统稳定，则$\underset{k\to \infty }{\lim }f(kT)=\underset{z\to 1}{\lim }(1-z^{-1})F(z)=\underset{z\to 1}{\lim }(z-1)F(z)$

求Z变换

1. 级数求和法
   即用定义硬算。
   
   注意级数求和要附加收敛条件。

2. 部分分式展开法
   即先分解，然后查表，再通过线性性质得出Z变换
   

Z变换表

求Z反变换

1. 长除法（幂级数展开法）
   简单易行，但因为难以找出规律，所以一般只用来计算前几项。
   步骤：分式除法，得到z的降幂序列。利用实位移性质写出对应的f(t)
   
   写成$f(kT)$序列形式和$f^{\ast }(t)$时域函数形式都可以。注意省略号不要丢了。

2. 部分分式展开法
   先分解，后查表。
   
   两个注意的地方：
   1.先除z，再进行计算。
   2.注意k的取值范围，选取原则是$e^{-akT}$是滞后的而不是超前的（非正幂）

3. 留数计算法
   $f(kT)=\sum _{i=1}^n\text{Res}[F(z)z^{k-1}{]}_{z\to p_i}$
   
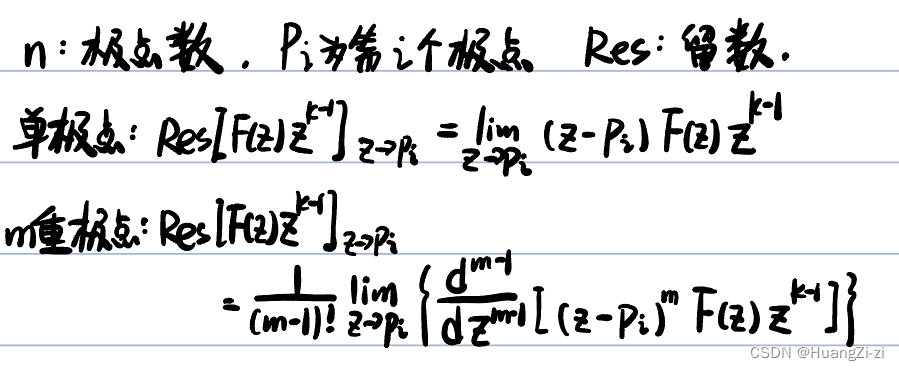
   即$F(z)$的z反变换等于$[F(z)z^{k-1}]$在各个极点处留数之和。
   例题：
   

用Z变换解差分方程

这个和用Laplace变换解微分方程是同样的思路。

脉冲传递函数

零初始条件下，线性定常系统，输出采样信号的Z变换与输入采样信号的Z变换之比，称为该系统的脉冲传递函数，或称Z传递函数
$G(z)=\frac{C(z)}{R(z)}$

注意：

• 先采样才有Z变换。因此要求输入、输出信号都为采样后信号。输出允许没有采样开关，但列写传递函数时必须设置虚拟采样开关，才能求出Z变换
• 传递函数与输入信号无关，但与采样周期有关

脉冲传递函数的求法：

1. 求系统脉冲响应，即为$G(s)$，求出：$g(t)={\mathcal{L}}^{-1}[G(s)]$
2. 采样：$g^{\ast }(t)={\sum }_{k=0}^{\infty }g(kT)\delta (t-kT)$
3. Z变换：$G(z)=Z[g^{\ast }(t)]={\sum }_{k=0}^{\infty }g(kT)z^{-k}$

脉冲传递函数与差分方程的相互转化

开环脉冲传递函数

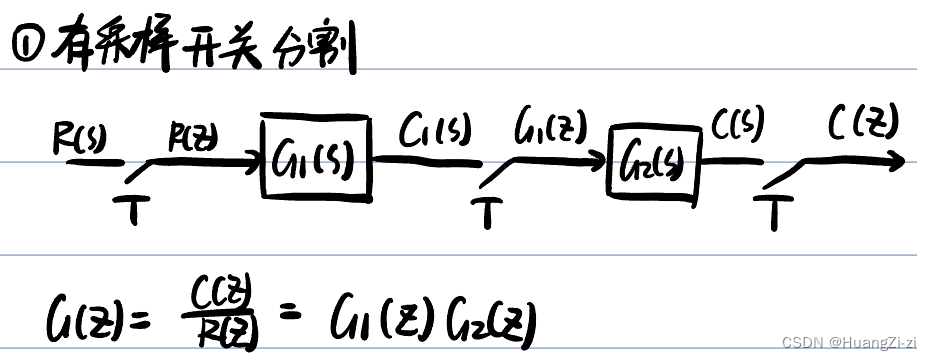
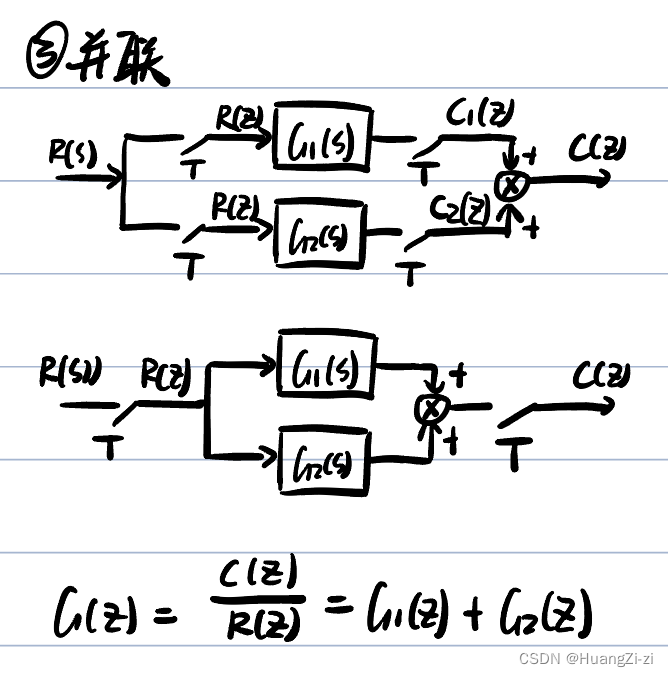
闭环脉冲传递函数

1. 采样开关在误差通道：
   
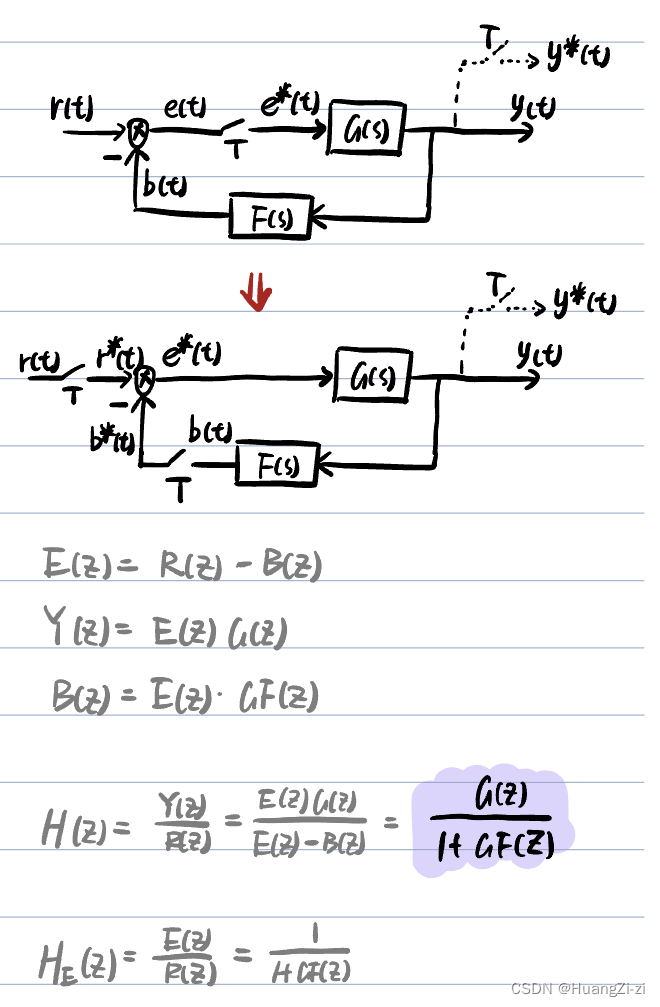
2. 一般情况
   很多情况下，因为R没有采样，被合并到其他地方先串连再Z变换，变成RG的形式，无法写出C/R的函数，所以改为写输出的函数。
   
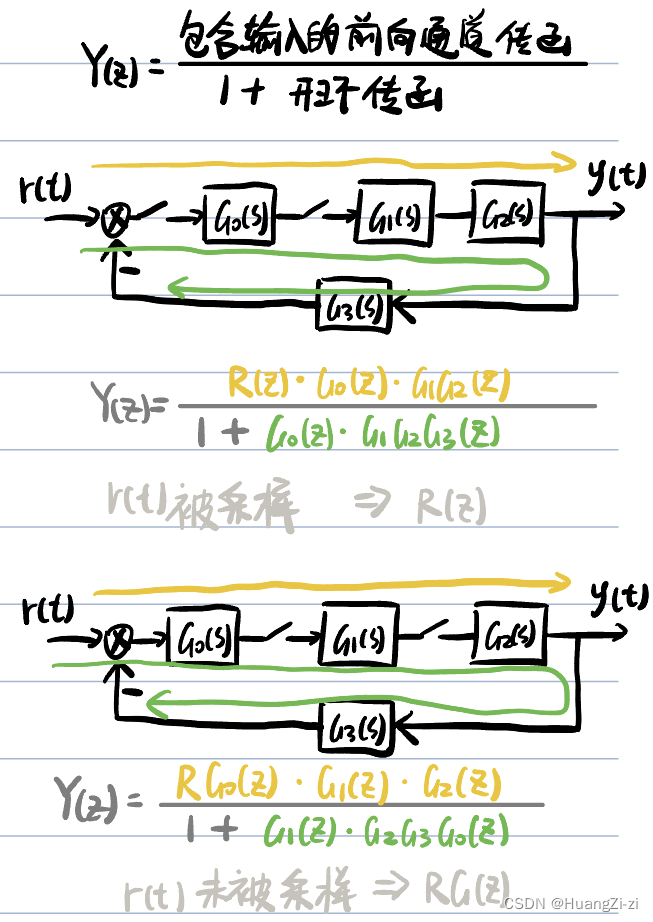
   这里注意，开环传函的列写，从某个采样开关开始，按照回路依次列写，直到回到这个采样开关。不必从R开始。

计算机控制系统的响应

其实本质就是Z反变换

这里得到的输出的采样值。

如果想要得到输出值，可以采取如下的方法：
$\begin{array}{rl}Y(s)=& G(s)E^{\ast }(s)\\ =& G(s)\frac{R^{\ast }(s)}{1+G{F}^{\ast }(s)}\\ y(t)=& {\mathcal{L}}^{-1}[Y(s)]\end{array}$