⭐作者介绍:大二本科网络工程专业在读,持续学习Java,努力输出优质文章
⭐作者主页:@逐梦苍穹
⭐所属专栏:数据结构。数据结构专栏主要是在讲解原理的基础上拿Java实现,有时候有C/C++代码。
⭐如果觉得文章写的不错,欢迎点个关注一键三连😉有写的不好的地方也欢迎指正,一同进步😁
目录
- 1、分析方法
- 2、常用分析方法
- 3、记法
- 4、常见大O阶
- 4.1、线性阶
- 4.2、平方阶
- 4.3、立方阶
- 4.4、对数阶
- 4.5、常数阶
- 5、java中常见内存占用
- 6、补充说明
1、分析方法
时间复杂度的分析方法可以分为事前分析法和事后分析法。
事前分析法是指在实际运行算法之前,通过分析算法的代码和数据结构,推算出算法的时间复杂度。这种方法可以在实际运行之前就预估算法的性能,帮助选择更优秀的算法。
常用的事前分析方法有渐进复杂度分析法、最坏情况分析法、平均情况分析法和最好情况分析法等。
事后分析法是指通过实际运行算法并记录其运行时间,来分析算法的时间复杂度。这种方法可以得到较为准确的结果,但需要先运行算法一次才能进行分析,不够高效。常用的事后分析方法有插值搜索和时间分析法。
插值搜索是一种基于二分查找的搜索方法,它通过在实际运行中采用不同规模的输入,得到不同规模下的运行时间,从而推算出算法在其他规模下的运行时间。这种方法需要预估出算法的时间复杂度,然后通过实验数据进行验证和推算。
时间分析法是一种基于运行时间的分析方法,它通过实际运行算法并记录每个操作所需的时间,然后对所有操作的时间进行统计和分析,得出算法的时间复杂度。这种方法需要考虑到不同操作的执行次数,需要对算法的实现进行较为详细的分析。
总的来说,事前分析法和事后分析法都是有效的时间复杂度分析方法,选择哪种方法取决于具体情况和需求。
2、常用分析方法
时间复杂度是衡量算法效率的一种方法,用于描述算法运行时间与输入规模之间的关系。通常用大O符号表示。
在分析时间复杂度时,一般可以采用以下几种方法:
- 最坏情况分析法
最坏情况分析法是一种保守的分析方法,它假设算法在最坏情况下所需的时间是算法在所有情况下所需时间的上界。这种方法通常用于保证算法在任何输入下都能保证一定的效率。 - 平均情况分析法
平均情况分析法是一种更为准确的分析方法,它考虑了算法在不同输入下的表现,并对每种输入进行加权平均。这种方法需要对输入数据的分布进行假设,因此需要较为严格的数学证明。 - 最好情况分析法
最好情况分析法是一种较为乐观的分析方法,它假设算法在最好情况下所需的时间是算法在所有情况下所需时间的下界。这种方法通常用于评估算法的最优性能。 - 渐进复杂度分析法
渐进复杂度分析法是一种简单而又常用的分析方法,它w忽略了算法的常数项和低次项,只关注算法在输入规模增大时的表现。这种方法一般采用大O符号表示算法的渐进时间复杂度,如O(1)、O(log n)、O(n)、O(nlogn)、O(n^2)等。
在实际分析中,可以结合以上方法,选择最适合的方法来分析算法的时间复杂度。需要注意的是,时间复杂度只是一种理论上的估计,实际运行效率还受到许多因素的影响,如算法实现方式、计算机硬件性能等。
3、记法
大O记法
定义:
在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随着n的变化情况并确定T(n)的量级。
算法的时间复杂度,就是算法的时间量度,记作:T(n)=O(f(n))。它表示随着问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐近时间复杂度,简称时间复杂度,其中f(n)是问题规模n的某个函数。
在这里,我们需要明确一个事情:执行次数=执行时间
用大写O()来体现算法时间复杂度的记法,我们称之为大O记法。一般情况下,随着输入规模n的增大,T(n)增长最慢的算法为最优算法。
算法的空间复杂度计算公式记作:S(n)=O(f(n)),其中n为输入规模,f(n)为语句关于n所占存储空间的函数。
基于我们对函数渐近增长的分析,推导大O阶的表示法有以下几个规则可以使用:
1.用常数1取代运行时间中的所有加法常数;
2.在修改后的运行次数中,只保留高阶项;
3.如果最高阶项存在,且常数因子不为1,则去除与这个项相乘的常数;
4、常见大O阶
| 大O阶 | 时间/空间复杂度 |
|---|---|
| 线性阶 | O(n) |
| 平方阶 | O(n^2) |
| 立方阶 | O(n^3) |
| 对数阶 | O(logn) |
| 常数阶 | O(1) |
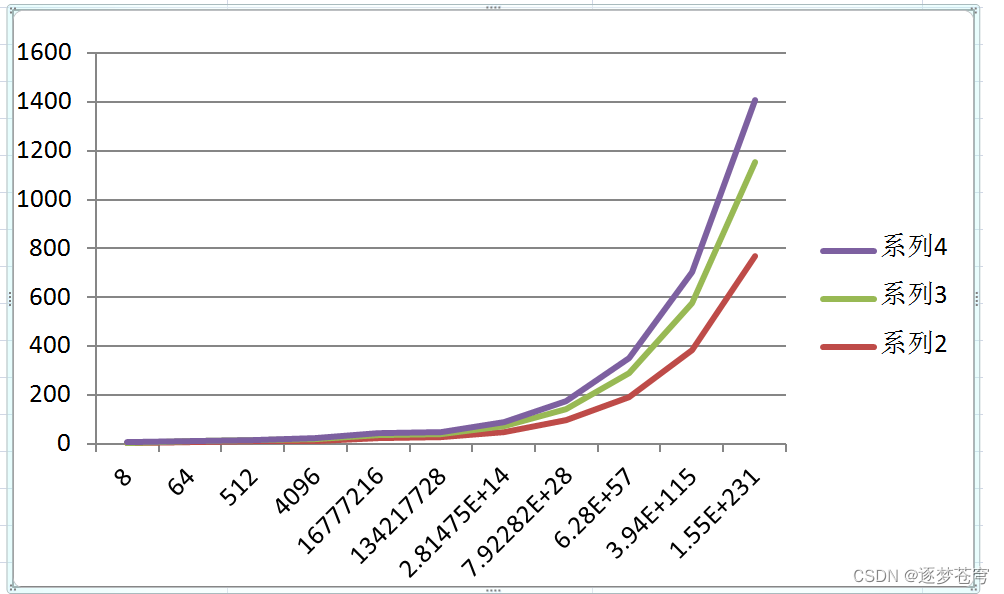
下面是对常见时间复杂度的一个总结:

他们的复杂程度从低到高依次为:
O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)
4.1、线性阶
一般含有非嵌套循环涉及线性阶,线性阶就是随着输入规模的扩大,对应计算次数呈直线增长,例如:

上面这段代码,它的循环的时间复杂度为O(n),因为循环体中的代码需要执行n次
4.2、平方阶
一般嵌套循环属于这种时间复杂度

上面这段代码,n=100,也就是说,外层循环每执行一次,内层循环就执行100次,那总共程序想要从这两个循环
中出来,就需要执行100*100次,也就是n的平方次,所以这段代码的时间复杂度是O(n^2)
4.3、立方阶
一般三层嵌套循环属于这种时间复杂度

上面这段代码,n=100,也就是说,外层循环每执行一次,中间循环循环就执行100次,中间循环每执行一次,最
内层循环需要执行100次,那总共程序想要从这三个循环中出来,就需要执行100100100次,也就是n的立方,所
以这段代码的时间复杂度是O(n^3)
4.4、对数阶

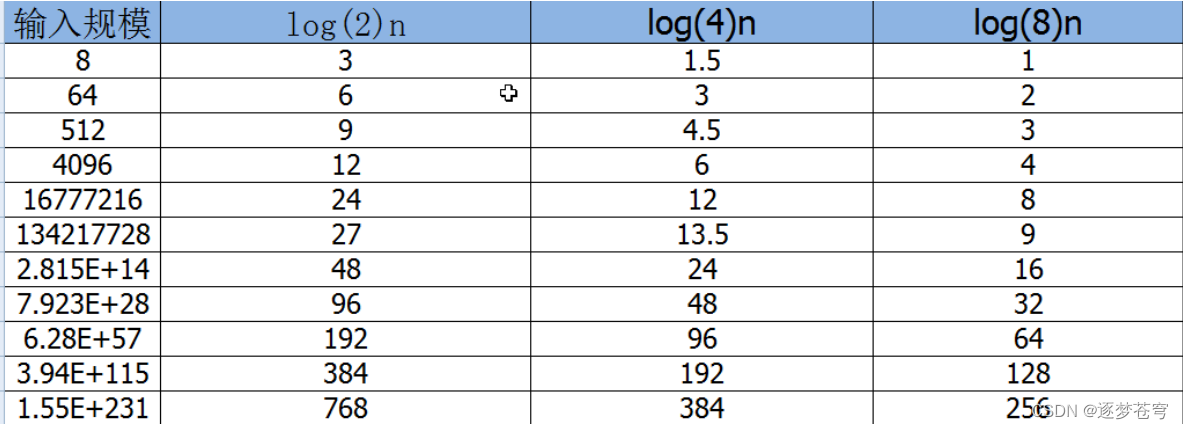
由于每次i*2之后,就距离n更近一步,假设有x个2相乘后大于n,则会退出循环。由于是2^x=n,得到x=log(2)n,所以这个循环的时间复杂度为O(logn);
对于对数阶,由于随着输入规模n的增大,不管底数为多少,他们的增长趋势是一样的,所以我们会忽略底数。
4.5、常数阶
一般不涉及循环操作的都是常数阶,因为它不会随着n的增长而增加操作次数。例如:

上述代码,不管输入规模n是多少,都执行2次,根据大O推导法则,常数用1来替换,所以上述代码的时间复杂度为O(1)
根据前面的折线图分析,我们会发现,从平方阶开始,随着输入规模的增大,时间成本会急剧增大,所以,我们的算法,尽可能的追求的是O(1),O(logn),O(n),O(nlogn)这几种时间复杂度,而如果发现算法的时间复杂度为平方阶、立方阶或者更复杂的,那我们可以认为这种算法是不可取的,需要优化。
5、java中常见内存占用
| 数据类型 | 内存占用字节数 |
|---|---|
| byte | 1 |
| short | 2 |
| int | 4 |
| long | 8 |
| float | 4 |
| double | 8 |
| boolean | 1 |
| char | 2 |
计算机访问内存的方式都是一次一个字节
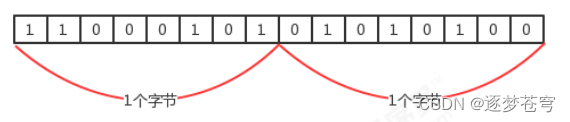
一个引用(机器地址)需要8个字节表示:
例如: Date date = new Date(),则date这个变量需要占用8个字节来表示
创建一个对象,比如new Date(),除了Date对象内部存储的数据(例如年月日等信息)占用的内存,该对象本身也有内存开销,每个对象的自身开销是16个字节,用来保存对象的头信息。
一般内存的使用,如果不够8个字节,都会被自动填充为8字节
6、补充说明
由于java中有内存垃圾回收机制,并且jvm对程序的内存占用也有优化(例如即时编译),我们无法精确的评估一个java程序的内存占用情况,但是了解了java的基本内存占用,使我们可以对java程序的内存占用情况进行估算。
由于现在的计算机设备内存一般都比较大,基本上个人计算机都是4G起步,大的可以达到32G,所以内存占用一般情况下并不是我们算法的瓶颈,普通情况下直接说复杂度,默认为算法的时间复杂度。