一 、GNN是怎么被提出来的？

比较常见的有CNN、RNN等。CNN的核心在于它的kernel，kernel在图片上平移，通过卷积的方式来提取特征。这里的关键在于图片结构上的平移不变性：一个小窗口无论移动到图片的哪一个位置，其内部的结构都是一模一样的，因此CNN可以实现参数共享。RNN针对的是自然语言这样的序列信息，是一个一维的结构。

但是在实际生活中，有很多不规则的结构，比如社交网络，分子结构等。图的结构是不规则的，没有平移不变性。简单来说，他也是一个特征提取器，只不过处理的对象是图数据。

图神经网络(GNN)可以解决的问题包括：节点分类、连接预测等。

二、GCN的思想

1、关键思想

基于附近的网络邻居生成节点的嵌入(embedding)表示。如下图所示，如果我们想要更新A点，那就要聚合一下它周围邻居的信息。

GCN模型可以有很多层。第K层的节点的嵌入表示是聚合第K-1层邻居的节点信息来计算得到的。其中，节点在第0层的嵌入表示就是节点特征(也就是这个点在最开始的时候含有的特征，它可能是多维的)。

更通俗的说，GCN的一个关键就是融合邻居的信息，那具体怎么来融合的，融合后进行什么操作？就是我们常听说的聚合与更新。

2、聚合与更新

 GCN在更新的时候，会加上自身的信息更新自身，如果这里不理解，下面会继续介绍。

3、简单理解

实际上无论经过多少层的GCN，最开始的图结构是不会被改变的，改变的是节点的信息，因为节点的信息一直在根据自己的邻居做更新。

 三、公式及其理解

太复杂的公式我也看不懂，但是我们把网络最基本的公式简单描述一下它的组成。

图神经网络的原型就是σ(AHW)这样的形势，跟上图对比，实际上是很像的。

本质就是邻接矩阵A和节点特征H，直接做内积，再乘一个参数矩阵W，然后激活一下，就相当于一个的神经网络层。就可以完成特征提取的工作了。

假设有一个图如下所示：

1、图结构的邻接矩阵A 和 图节点特征H

先说A，在上面已经给图的各个点进行编号，如果两个点之间有链接就是1，没有连接就是0。这个过程就是把图数据转化为邻接矩阵。

再说H，假如节点是有特征的，那么邻接矩阵就不能完整表达一个图结构，所以加入节点的特征矩阵。节点特征对于社交网络来说，可以是用户的身高、性别、年龄等；对于生物信息来说可以是基因表达矩阵等。

节点特征包含几列，取决于节点特征向量的长度，在下图中，特征向量的长度就是2。

如果 A 与 H 矩阵相乘(也就是说，节点与邻居相乘)，这时候并没有把自身的信息保留下来，所以加入自连接。

2、有自连接的邻接矩阵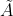

它的作用就是上文所说的，加上自身的信息更新自身。

3、有自连接的邻接矩阵的度矩阵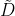

 这里的数值表示的是，包含的连接的节点和自连接本身。

4、为什么需要有自连接的邻接矩阵的度矩阵?

A是没有经过归一化的矩阵，这样与特征矩阵H相乘会改变特征原本的分布，所以对A做一个标准化处理。平衡度很大的节点的重要性。(对称归一化拉普拉斯矩阵)

四、参考链接

GCN（图卷积）--简书

GCN 图卷积网络---哔哩哔哩

The challenges of using graphs in machine learning