目录
一、相同的树
二、另一棵树的子树
三、翻转二叉树
四、平衡二叉树
五、对称二叉树
一、相同的树
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。 如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
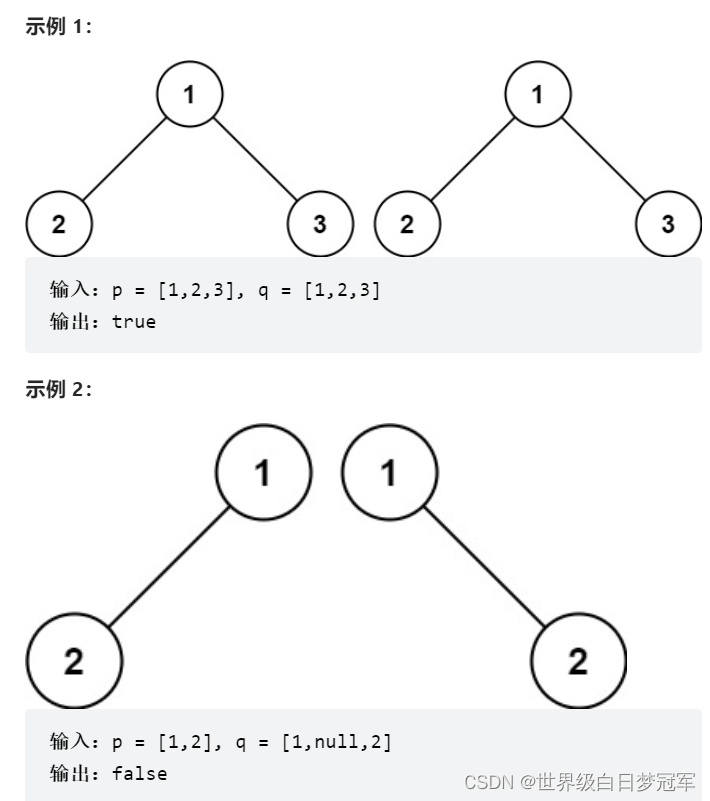
首先判断两个相同的树要先判断他的根节点,如果q和p的根节点都为空,那么他俩是相同的返回true;如果q为空p不为空或者p为空q不为空则不相同返回false;如果两者都不是空的那么就需要比较两者的val如果相等,那么可以进行下一步比较比较它们的左右子树,如果最后返回的都是true才是相同的树,只要有一个是false,那么就不相同。
public boolean isSameTree(TreeNode p, TreeNode q) {
if(p==null&&q!=null||p!=null&&q==null){
return false;
}
if(p==null&&q==null){
return true;
}
if(p.val!=q.val){
return false;
}
return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);
}二、另一棵树的子树
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。 二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
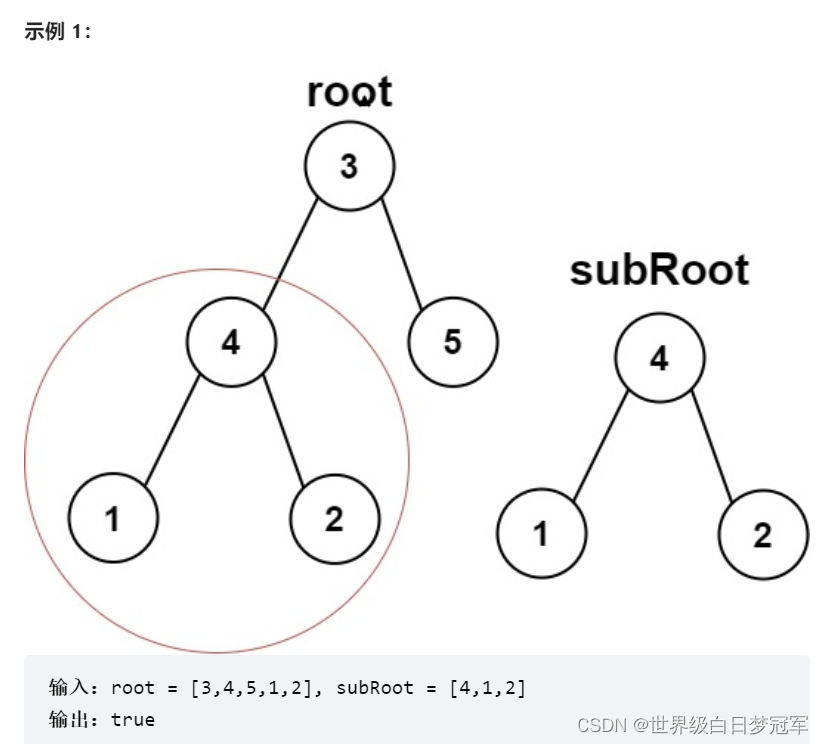
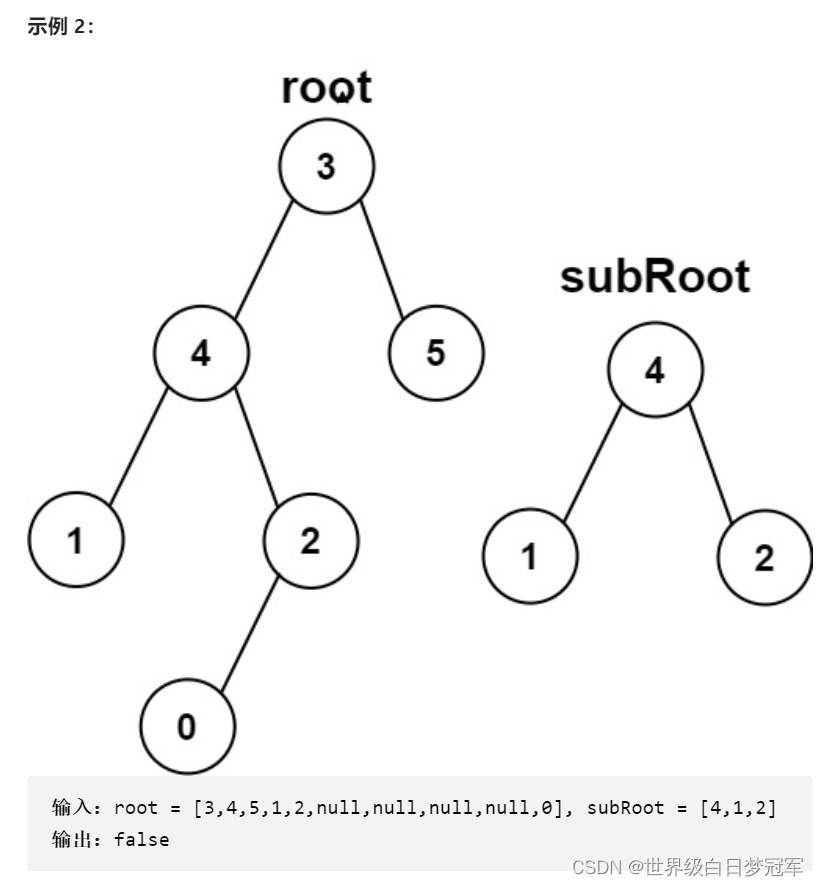
先判断树根root和subRoot是否是相同的树,若是直接return true;否则判断左子树是否包含subRoot或在右子树中是否包含subRoot,只要有一个子树中有包含关系则返回true。
所以在这道题中我们需要用到第一道题的isSameTree方法,用于第一步判断 树根root和subRoot是否是相同的树。
这两道题都是前序遍历的问题,都是从跟结点出发。
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
if(root==null&&subRoot==null){
return true;
}
if(root==null||subRoot==null){
return false;
}
if(isSameTree(root,subRoot)){
return true;
}
return isSubtree(root.left,subRoot)||isSubtree(root.right,subRoot);
}
public boolean isSameTree(TreeNode p, TreeNode q) {
if(p==null&&q!=null||p!=null&&q==null){
return false;
}
if(p==null&&q==null){
return true;
}
if(p.val!=q.val){
return false;
}
return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);
}三、翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
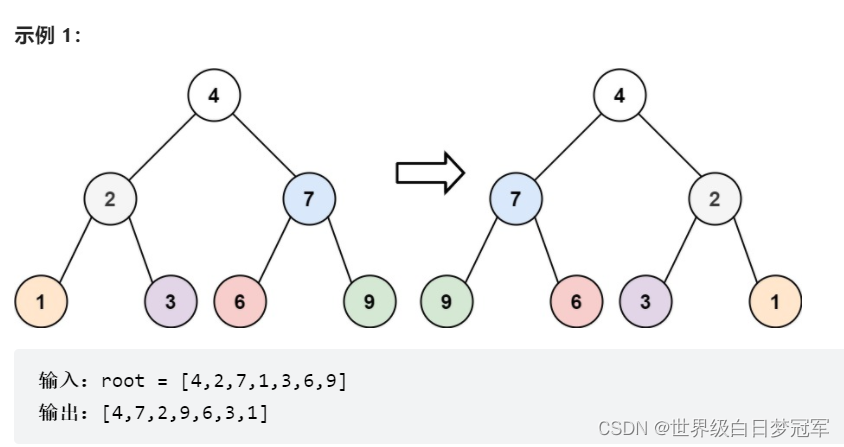
先将所有子树翻转完毕,最后交换2和7两个的顺序。
这个方法采用后续遍历,首先先判断树是否为空或者只有一个结点,这两种情况都不需要再进行翻转,直接返回root即可。然后我们先进行子树的翻转,最后在交换处理后的左右子树即可。然后返回根节点。
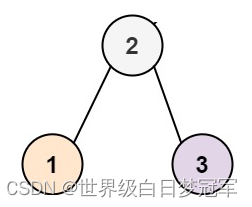
首先我们进入整个方法,判断递归结束条件不满足后,往下走,走到root.left = invertTree(root.left); 这时root的树是如图1所示的,
紧接着在进入root.left = invertTree(root.left); 这时root树入图2所示,这时他只有一个结点,所以返回root。
然后我们进入root.right = invertTree(root.right);这时图3就是现在的root,这时也只有一个结点所以返回root。
然后我们就进入将根节点为2的数翻转的操作。翻转成功后如图4,然后返回root。
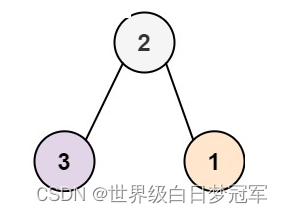
紧接着对根节点的右子树进行翻转,反转后的结果如下。
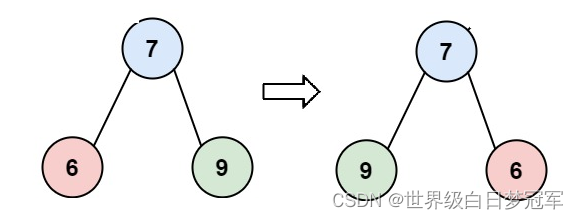
最后回到根节点,将上述两个反转好的左右子树根节点在进行翻转,就得到了整个二叉树的翻转。
public TreeNode invertTree(TreeNode root) {
if (root == null || (root.left == null && root.right == null)) {
return root;
}
root.left = invertTree(root.left);
root.right = invertTree(root.right);
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
return root;
}四、平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。 本题中,一棵高度平衡二叉树定义为: 一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
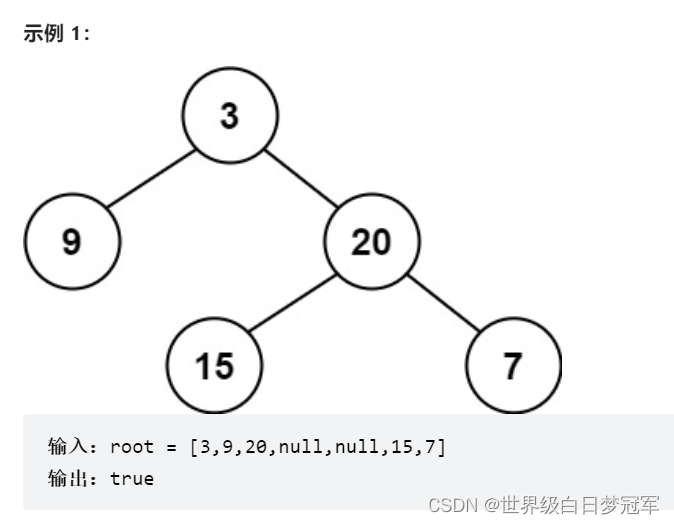
首先排除掉树为空和只有一个节点的情况,这两种情况一定是平衡树。
然后利用求树的高度的方法,求出左子树和右子树的高度差值是否小于等于一,如果满足条件那么继续递归查看左子树和右子树这两棵树是否也满足平衡树的条件;如果大于一那么直接返回false。
public boolean isBalanced(TreeNode root) {
if (root==null||(root.left==null&&root.right==null)){
return true;
}
int leftHeight = height(root.left);
int rightHeight = height(root.right);
int abs = Math.abs(leftHeight-rightHeight);
if(abs>1){
return false;
}
return isBalanced(root.right)&&isBalanced(root.left);
}
public int height(TreeNode root){
if(root==null){
return 0;
}
if(root.left==null&&root.right==null){
return 1;
}
return 1+Math.max(height(root.left),height(root.right));
}五、对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
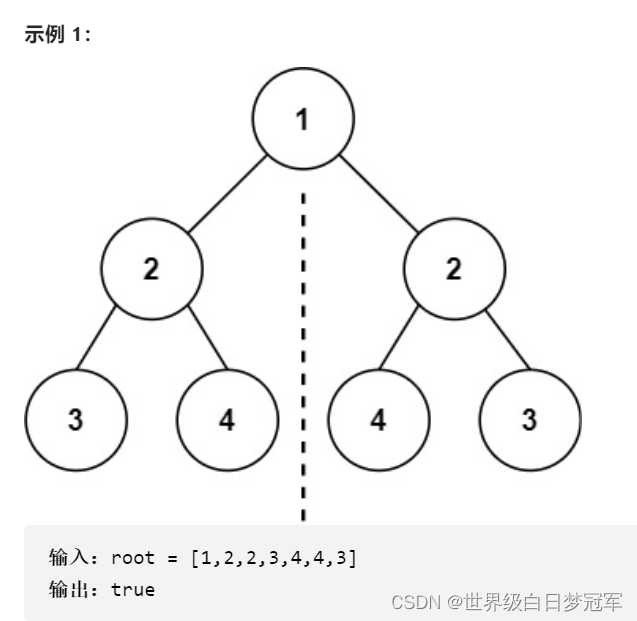
首先系统规定这个树不是空树,所以我们直接创建一个方法isMirror来判断树的左右子树是否是镜像的,直接传入root.left,root.right。
若t1==null&&t2==null那么一定是镜像的,所以返回true,排除这个之后如果t1==null||t2==null,那么一定有一个非空则不是镜像的则返回false。接下来如果t1.val != t2.val,那么也不是镜像的直接返回false,当这三个条件都结束后,则对t1.left和t2.right、t1.right和t2.left在进行镜像对比。
所以首先进入isMirror方法t1和t2如图所示,他们两个的值相等,满足进入递归的条件,则对比他们的左右节点的镜像关系。
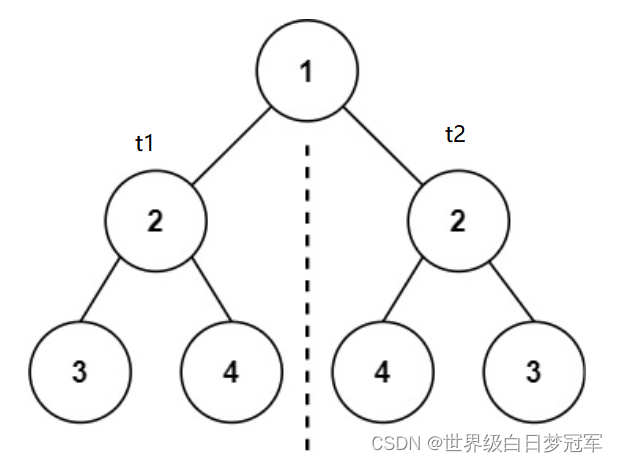
isMirror(t1.left, t2.right) 和isMirror(t1.right, t2.left)调用递归的t1和t2分别如下图所示,对比他们是否为镜像关系。
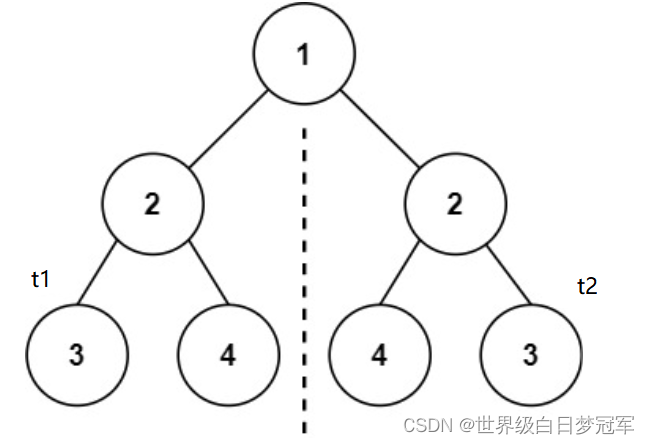
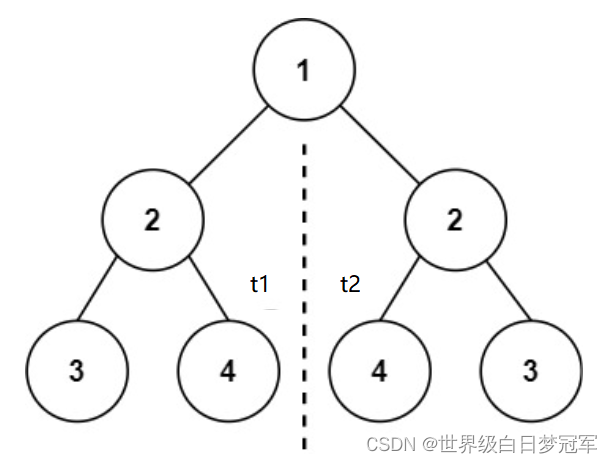
如果都为镜像关系那么整个树就是对称的。
public boolean isSymmetric(TreeNode root) {
return isMirror(root.left,root.right);
}
public boolean isMirror(TreeNode t1,TreeNode t2) {
if(t1==null&&t2==null){
return true;
}
if(t1==null||t2==null){
return false;
}
if (t1.val != t2.val) {
return false;
}
return isMirror(t1.left, t2.right) && isMirror(t1.right, t2.left);
}